5.3.1平行线的性质(第2课时) 知识点导学导练+检测(含答案)
文档属性
| 名称 | 5.3.1平行线的性质(第2课时) 知识点导学导练+检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 106.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 16:05:52 | ||
图片预览


文档简介
5.3.1平行线的性质(第2课时)
双基导学导练
知识点 平行线的判定与性质的综合运用
1.(2018襄阳)如图1, BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠ABD的度数为 . ∠BEC的度数为 .
2.(2017荆州)一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图2所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点M,且∠CDE=40°,则∠BFM的度数为 .
3.(2018十堰)如图3,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB的度数为( )
A.40° B.50° C.60° D.70°
4.如图4,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=220°,则∠BOC的度数为( )
A.110° B.120° C.130° D.140°
5.(2017江岸)填空并完成推理过程.
如图5,E点为DF上的点,B点为AC上的点,∠1=∠2,∠C=∠D,试说明:AC∥DF.
6.(2018黄陂)如图6,∠AOB内有一点P
(1)过点P作PC∥OA交OB于点C,作PD∥OB交OA于点D,作PE⊥OB于点E
(2)在(1)的条件下,若∠AOB=40°,求∠CPE的度数
真题检测反馈
7.(2017武昌)若∠A与∠B的两边分别平行,若∠A=60°,则∠B的度数为( )
A.120° B.60° C.30°或150° D.60°或120°
8.(2018江西如图7,将一副三角板和张对边平行的纸条按下列方式摆放,两个三角板的直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是 。
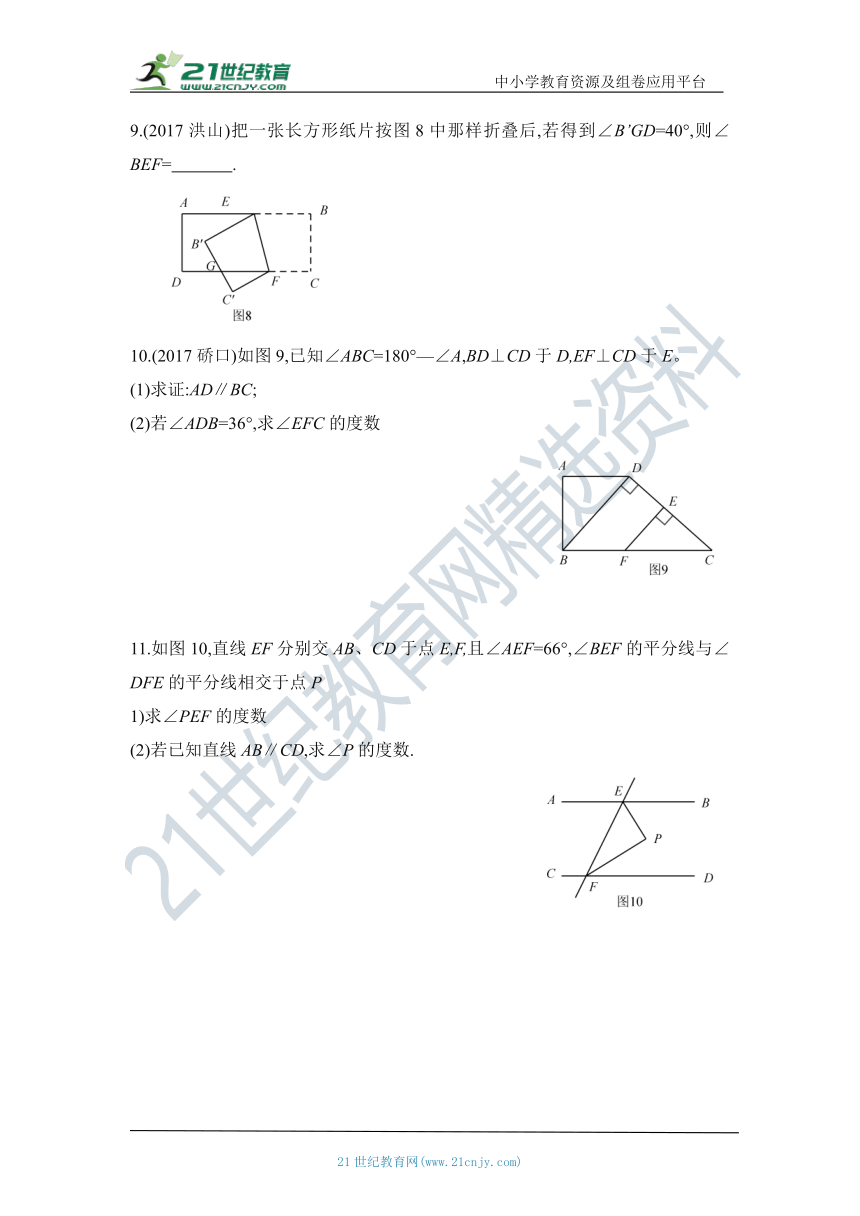
9.(2017洪山)把一张长方形纸片按图8中那样折叠后,若得到∠B’GD=40°,则∠BEF= .
10.(2017硚口)如图9,已知∠ABC=180°—∠A,BD⊥CD于D,EF⊥CD于E。
(1)求证:AD∥BC;
(2)若∠ADB=36°,求∠EFC的度数
11.如图10,直线EF分别交AB、CD于点E,F,且∠AEF=66°,∠BEF的平分线与∠DFE的平分线相交于点P
1)求∠PEF的度数
(2)若已知直线AB∥CD,求∠P的度数.
创新拓展提升
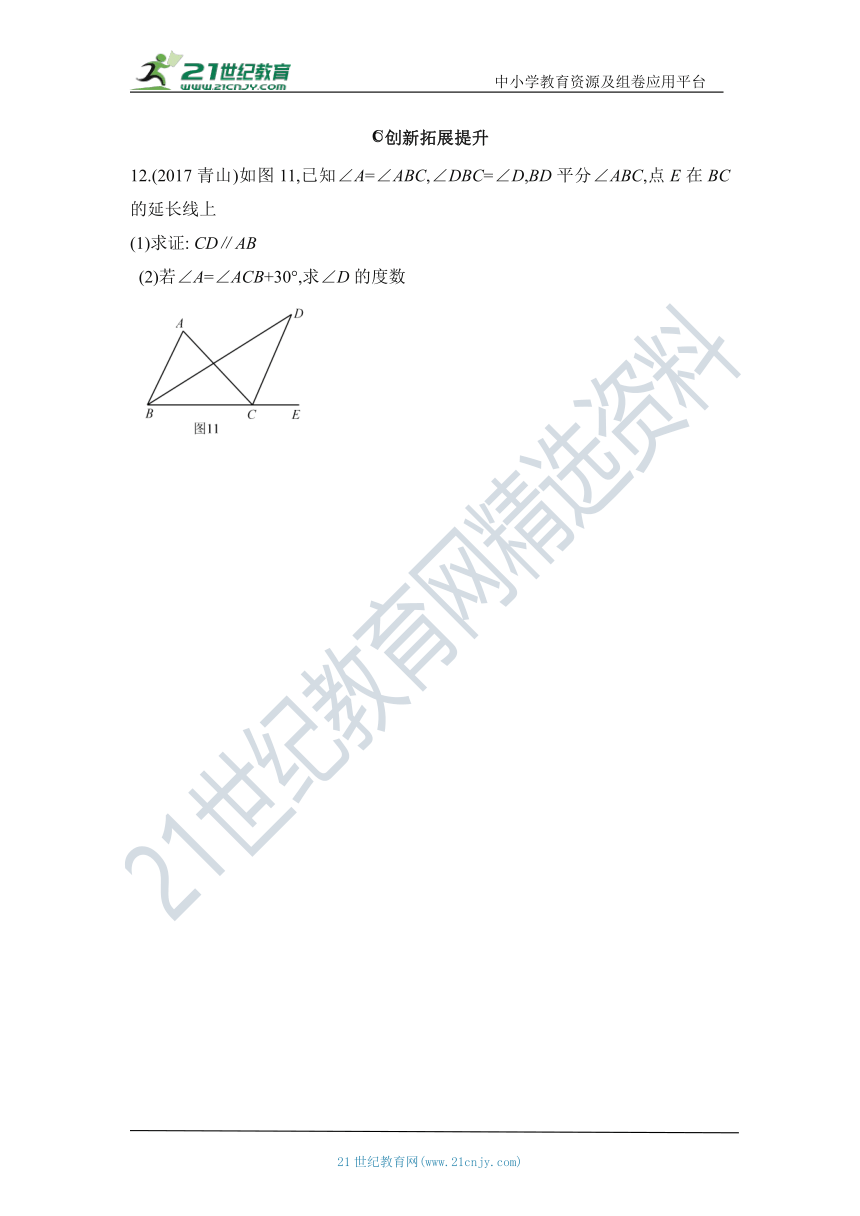
12.(2017青山)如图11,已知∠A=∠ABC,∠DBC=∠D,BD平分∠ABC,点E在BC的延长线上
(1)求证: CD∥AB
(2)若∠A=∠ACB+30°,求∠D的度数
5.3.1平行线的性质(第2课时)
双基导学导练
知识点 平行线的判定与性质的综合运用
1.(2018襄阳)如图1, BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠ABD的度数为 . ∠BEC的度数为 .
答案:130°;115°
2.(2017荆州)一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图2所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点M,且∠CDE=40°,则∠BFM的度数为 .
答案:140°
3.(2018十堰)如图3,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB的度数为( )
A.40° B.50° C.60° D.70°
答案:B
4.如图4,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=220°,则∠BOC的度数为( )
A.110° B.120° C.130° D.140°
答案:A
5.(2017江岸)填空并完成推理过程.
如图5,E点为DF上的点,B点为AC上的点,∠1=∠2,∠C=∠D,试说明:AC∥DF.
证明:∵∠1=∠2(已知) ∠1=∠3(对顶角相等)
∵∠2=∠3(等量代换)
∴BD∥CE(同位角相等,两直线平行)
∴∠C=∠ABD两直线平行,同位角相等)
又∵∠C=∠D(已知)
∴∠D=∠ABD(等量代换)
∴AC∥DF(内错角相等,两直线平行)
6.(2018黄陂)如图6,∠AOB内有一点P
(1)过点P作PC∥OA交OB于点C,作PD∥OB交OA于点D,作PE⊥OB于点E
(2)在(1)的条件下,若∠AOB=40°,求∠CPE的度数
解:(1)画图略
(2)∵∠AOB=40°,DP∥OB
∴∠ADP=∠AOB=40° ∵PC∥AO ∴∠CPD=∠ADP=40°
∵EP⊥OB ∴∠BEP=90°
又∴DP∥OB ∵∠DPE=∠BEP=90°
∴ ∠CPE=∠DPE-∠DPC=90°-40°=50°
真题检测反馈
7.(2017武昌)若∠A与∠B的两边分别平行,若∠A=60°,则∠B的度数为( )
A.120° B.60° C.30°或150° D.60°或120°
答案:D
8.(2018江西如图7,将一副三角板和张对边平行的纸条按下列方式摆放,两个三角板的直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是 。
答案:15°
9.(2017洪山)把一张长方形纸片按图8中那样折叠后,若得到∠B’GD=40°,则∠BEF= .
答案:65°
10.(2017硚口)如图9,已知∠ABC=180°—∠A,BD⊥CD于D,EF⊥CD于E。
(1)求证:AD∥BC;
(2)若∠ADB=36°,求∠EFC的度数
(1)证明:∵∠ABC=180°—∠A ∴∠ABC+∠A=180°∴AD∥BC
(2)解:∵BD⊥CD,EF⊥CD
∵.∠BDC=∠FEC=90° ∴BD∥FE ∴∠EFC=∠DBC
又∴AD∥BC∴,∠DBC=∠ADB=36°∴EFC=∠DBC=36°
11.如图10,直线EF分别交AB、CD于点E,F,且∠AEF=66°,∠BEF的平分线与∠DFE的平分线相交于点P
1)求∠PEF的度数
(2)若已知直线AB∥CD,求∠P的度数.
解:(1)∠AEF=66°∴∠BEF=180°—∠AEF=180°-66°=114°
又:EP平分∠BEF∴∠PEF=∠PEB=∠BEF=57°
(2)过点P作PQ∥AB∵AB∥CD,PQ∥CD∴,∠EPQ=∠PEB=57°,∠FPQ=∠PFD
AB∥CD∴∠DFE=∠AEF=66° FP平分∠DFE ∴∠PFD= false∠DFE=33°
∠FPQ=33°∴∠EPF=∠EPQ+∠FPQ=57°+33°=90°
创新拓展提升
12.(2017青山)如图11,已知∠A=∠ABC,∠DBC=∠D,BD平分∠ABC,点E在BC的延长线上
(1)求证: CD∥AB
(2)若∠A=∠ACB+30°,求∠D的度数
(1)证明:∵BD平分∠ABC ∴∠ABD=∠CBD
∵∠DBC=∠D∴∠ABD=∠D∴CD∥AB
(2)解:∵AB∥CD∴∠DCA=∠CAB,∠DCE=∠ABC
∵∠ACB+∠ACD+∠DCE=180°
∴∠ACB+30°+∠ACB十30°十∠ACB=180°∴∠ACB=40°∴∠A=40°+30°=70°
∠D=∠ABD=false<ABC=false∠A=35°
双基导学导练
知识点 平行线的判定与性质的综合运用
1.(2018襄阳)如图1, BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠ABD的度数为 . ∠BEC的度数为 .
2.(2017荆州)一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图2所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点M,且∠CDE=40°,则∠BFM的度数为 .
3.(2018十堰)如图3,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB的度数为( )
A.40° B.50° C.60° D.70°
4.如图4,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=220°,则∠BOC的度数为( )
A.110° B.120° C.130° D.140°
5.(2017江岸)填空并完成推理过程.
如图5,E点为DF上的点,B点为AC上的点,∠1=∠2,∠C=∠D,试说明:AC∥DF.
6.(2018黄陂)如图6,∠AOB内有一点P
(1)过点P作PC∥OA交OB于点C,作PD∥OB交OA于点D,作PE⊥OB于点E
(2)在(1)的条件下,若∠AOB=40°,求∠CPE的度数
真题检测反馈
7.(2017武昌)若∠A与∠B的两边分别平行,若∠A=60°,则∠B的度数为( )
A.120° B.60° C.30°或150° D.60°或120°
8.(2018江西如图7,将一副三角板和张对边平行的纸条按下列方式摆放,两个三角板的直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是 。
9.(2017洪山)把一张长方形纸片按图8中那样折叠后,若得到∠B’GD=40°,则∠BEF= .
10.(2017硚口)如图9,已知∠ABC=180°—∠A,BD⊥CD于D,EF⊥CD于E。
(1)求证:AD∥BC;
(2)若∠ADB=36°,求∠EFC的度数
11.如图10,直线EF分别交AB、CD于点E,F,且∠AEF=66°,∠BEF的平分线与∠DFE的平分线相交于点P
1)求∠PEF的度数
(2)若已知直线AB∥CD,求∠P的度数.
创新拓展提升
12.(2017青山)如图11,已知∠A=∠ABC,∠DBC=∠D,BD平分∠ABC,点E在BC的延长线上
(1)求证: CD∥AB
(2)若∠A=∠ACB+30°,求∠D的度数
5.3.1平行线的性质(第2课时)
双基导学导练
知识点 平行线的判定与性质的综合运用
1.(2018襄阳)如图1, BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠ABD的度数为 . ∠BEC的度数为 .
答案:130°;115°
2.(2017荆州)一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图2所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点M,且∠CDE=40°,则∠BFM的度数为 .
答案:140°
3.(2018十堰)如图3,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB的度数为( )
A.40° B.50° C.60° D.70°
答案:B
4.如图4,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=220°,则∠BOC的度数为( )
A.110° B.120° C.130° D.140°
答案:A
5.(2017江岸)填空并完成推理过程.
如图5,E点为DF上的点,B点为AC上的点,∠1=∠2,∠C=∠D,试说明:AC∥DF.
证明:∵∠1=∠2(已知) ∠1=∠3(对顶角相等)
∵∠2=∠3(等量代换)
∴BD∥CE(同位角相等,两直线平行)
∴∠C=∠ABD两直线平行,同位角相等)
又∵∠C=∠D(已知)
∴∠D=∠ABD(等量代换)
∴AC∥DF(内错角相等,两直线平行)
6.(2018黄陂)如图6,∠AOB内有一点P
(1)过点P作PC∥OA交OB于点C,作PD∥OB交OA于点D,作PE⊥OB于点E
(2)在(1)的条件下,若∠AOB=40°,求∠CPE的度数
解:(1)画图略
(2)∵∠AOB=40°,DP∥OB
∴∠ADP=∠AOB=40° ∵PC∥AO ∴∠CPD=∠ADP=40°
∵EP⊥OB ∴∠BEP=90°
又∴DP∥OB ∵∠DPE=∠BEP=90°
∴ ∠CPE=∠DPE-∠DPC=90°-40°=50°
真题检测反馈
7.(2017武昌)若∠A与∠B的两边分别平行,若∠A=60°,则∠B的度数为( )
A.120° B.60° C.30°或150° D.60°或120°
答案:D
8.(2018江西如图7,将一副三角板和张对边平行的纸条按下列方式摆放,两个三角板的直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是 。
答案:15°
9.(2017洪山)把一张长方形纸片按图8中那样折叠后,若得到∠B’GD=40°,则∠BEF= .
答案:65°
10.(2017硚口)如图9,已知∠ABC=180°—∠A,BD⊥CD于D,EF⊥CD于E。
(1)求证:AD∥BC;
(2)若∠ADB=36°,求∠EFC的度数
(1)证明:∵∠ABC=180°—∠A ∴∠ABC+∠A=180°∴AD∥BC
(2)解:∵BD⊥CD,EF⊥CD
∵.∠BDC=∠FEC=90° ∴BD∥FE ∴∠EFC=∠DBC
又∴AD∥BC∴,∠DBC=∠ADB=36°∴EFC=∠DBC=36°
11.如图10,直线EF分别交AB、CD于点E,F,且∠AEF=66°,∠BEF的平分线与∠DFE的平分线相交于点P
1)求∠PEF的度数
(2)若已知直线AB∥CD,求∠P的度数.
解:(1)∠AEF=66°∴∠BEF=180°—∠AEF=180°-66°=114°
又:EP平分∠BEF∴∠PEF=∠PEB=∠BEF=57°
(2)过点P作PQ∥AB∵AB∥CD,PQ∥CD∴,∠EPQ=∠PEB=57°,∠FPQ=∠PFD
AB∥CD∴∠DFE=∠AEF=66° FP平分∠DFE ∴∠PFD= false∠DFE=33°
∠FPQ=33°∴∠EPF=∠EPQ+∠FPQ=57°+33°=90°
创新拓展提升
12.(2017青山)如图11,已知∠A=∠ABC,∠DBC=∠D,BD平分∠ABC,点E在BC的延长线上
(1)求证: CD∥AB
(2)若∠A=∠ACB+30°,求∠D的度数
(1)证明:∵BD平分∠ABC ∴∠ABD=∠CBD
∵∠DBC=∠D∴∠ABD=∠D∴CD∥AB
(2)解:∵AB∥CD∴∠DCA=∠CAB,∠DCE=∠ABC
∵∠ACB+∠ACD+∠DCE=180°
∴∠ACB+30°+∠ACB十30°十∠ACB=180°∴∠ACB=40°∴∠A=40°+30°=70°
∠D=∠ABD=false<ABC=false∠A=35°
