5.1.1相交线 知识点导学导练+检测(含答案)
文档属性
| 名称 | 5.1.1相交线 知识点导学导练+检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 167.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 15:54:54 | ||
图片预览



文档简介
5.1.1 相交线
A.双基导学导练
知识点1 邻补角的定义及其性质
1.两个角有一条__________,它们的另一条边互为_________,具有这种关系的__________,________邻补角.
2.邻补角与补角的主要区别是:补角只反映两个角之间的数量关系,即__________________;而邻补角是补角的特殊情况,邻补角既有数量关系:_________________,又要有位置关系:_________________________.
3.如图1,直线AB、CD交于点O,射线OM平分∠AOC,若∠AOM=42°,则∠BOC的度数为______.
4.如图2,已知直线AB、CD交于点O,且OE平分∠BOC.
(1)直接写出∠AOC的邻补角;(2)写出∠EOA的补角,并说明理由;
(3)若∠AOC=42°,求∠BOE的度数.
知识点2 对顶角的定义及其性质
5.下列说法:①有公共顶点,没有公共边的两个角是对顶角;②相等的两个角是对顶角;③如果两个角是对顶角,那么这两个角相等;④如果一个角的两边分别是另一个角两边的反向延长线,那么这两个角是对顶角.其中正确的个数为( )
A.1 B.2 C.3 D.4
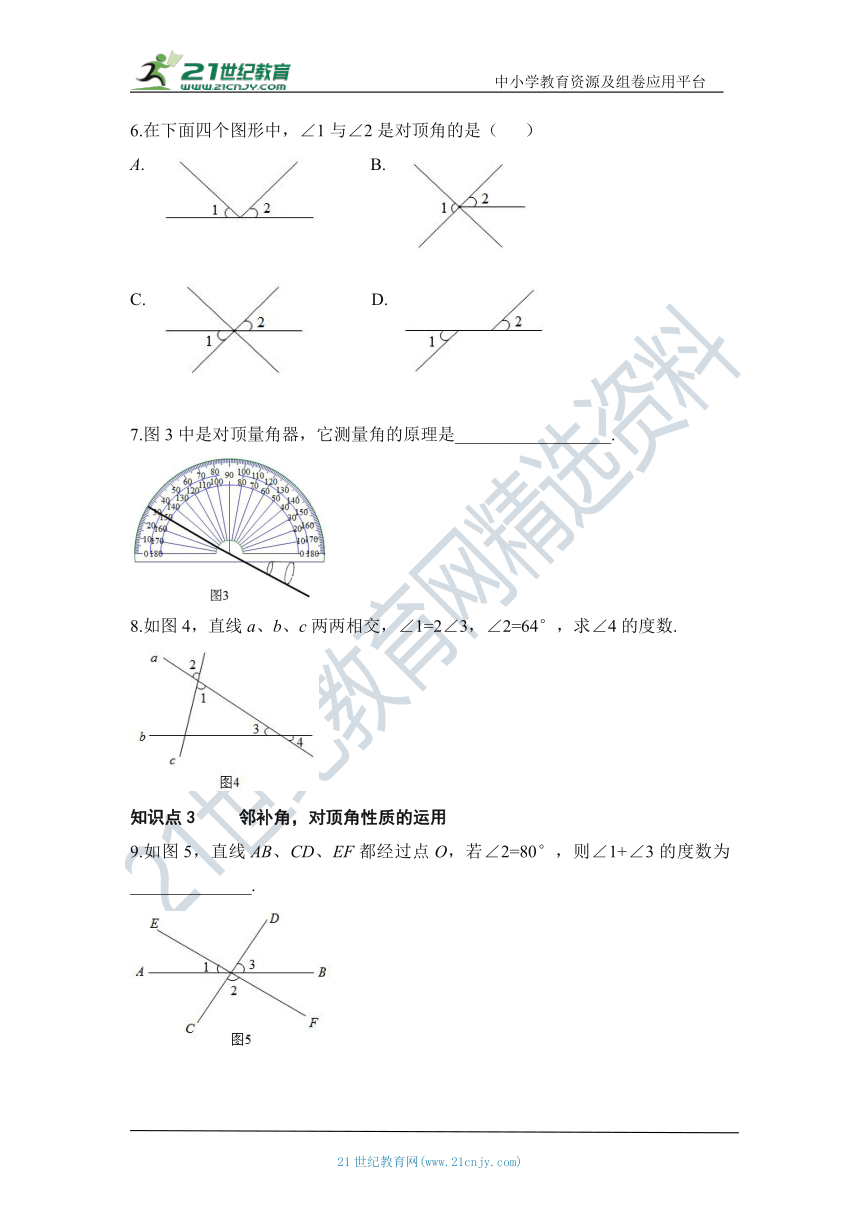
6.在下面四个图形中,∠1与∠2是对顶角的是( )
24028407683522796599695A. B.
2361565501652374901905C. D.
7.图3中是对顶量角器,它测量角的原理是__________________.
8.如图4,直线a、b、c两两相交,∠1=2∠3,∠2=64°,求∠4的度数.
知识点3 邻补角,对顶角性质的运用
9.如图5,直线AB、CD、EF都经过点O,若∠2=80°,则∠1+∠3的度数为______________.
10.如图6,直线AB、CD相交于点O,OE平分∠BOD,若∠3:∠2=8:1,求∠AOC的度数.
11.(2018武汉十一初)如图7,直线AB,CD相交于点O,OE平分∠BOD,若∠3:∠2=8:1,求∠AOC的度数.
B.真题检测反馈
12.如图8,直线AB、CD、EF相交于点O,则∠BOE的对顶角是________,∠COF的邻补角是__________;若∠AOC:∠AOE=2:3,∠EOD=130°,则∠BOC=_________.
13.如图9,已知∠AOB与∠BOE互为邻补角,且∠BOC>∠AOB,OD平分∠AOB,射线OE使∠BOE=false∠EOC,当∠DOE=72°时,则∠EOC的度数为_________.
14.将一张长方形纸片按如图10所示的方式折叠(射线false经过点false),BC、BD为折痕,求∠CBD的度数.
C.创新拓展提升
15.(1)两条直线相交于一点有_____组不同的对顶角;(2)三条直线相交于一点有_____组不同的对顶角;(3)四条直线相交于一点有_______组不同的对顶角;(4)n条直线相交于一点有________组不同的对顶角.
16.一条直线最多将平面分成两部分,两条直线最多将平面分成4部分,三条直线最多将平面分成7部分,四条直线最多将平面分成_____部分,...,则8条直线最多将平面分成______部分.
5.1.1 相交线
A.双基导学导练
知识点1 邻补角的定义及其性质
1.两个角有一条__________,它们的另一条边互为_________,具有这种关系的__________,________邻补角.
答案:公共边;反向延长线;两个角;互为
2.邻补角与补角的主要区别是:补角只反映两个角之间的数量关系,即__________________;而邻补角是补角的特殊情况,邻补角既有数量关系:_________________,又要有位置关系:_________________________.
答案:两角之和等于180度;两角之和等于180度;两角有公共的顶点和公共的边且另一半互为反向延长线
3.如图1,直线AB、CD交于点O,射线OM平分∠AOC,若∠AOM=42°,则∠BOC的度数为______.
答案:96°
4.如图2,已知直线AB、CD交于点O,且OE平分∠BOC.
(1)直接写出∠AOC的邻补角;(2)写出∠EOA的补角,并说明理由;
(3)若∠AOC=42°,求∠BOE的度数.
解:(1)∠AOC的邻补角是∠AOD,∠COB
(2)∵∠AOE+∠EOB=180° ∴∠EOA与∠EOB互补
又∵∠EOB=∠COE ∴∠AOE+∠COE=180° ∴∠AOE与∠COE也互补
(3)∵∠AOC+∠BOC=180° ∴∠BOC=180°-∠AOC=180°-42°=138°
又∵OE平分∠COB ∴∠BOE=false∠COB=69°
知识点2 对顶角的定义及其性质
5.下列说法:①有公共顶点,没有公共边的两个角是对顶角;②相等的两个角是对顶角;③如果两个角是对顶角,那么这两个角相等;④如果一个角的两边分别是另一个角两边的反向延长线,那么这两个角是对顶角.其中正确的个数为( )
A.1 B.2 C.3 D.4
答案:B
6.在下面四个图形中,∠1与∠2是对顶角的是( )
262128083185167640146050A. B.
231140272415
260540510160C. D.
答案:C
7.图3中是对顶量角器,它测量角的原理是__________________.
答案:对顶角相等
8.如图4,直线a、b、c两两相交,∠1=2∠3,∠2=64°,求∠4的度数.
解:∵∠2=65°,∴∠1=∠2=64°,又∵∠1=2∠3 ,∴∠3=false∠1=false×64°=32°,∴∠4=∠3=32°
知识点3 邻补角,对顶角性质的运用
9.如图5,直线AB、CD、EF都经过点O,若∠2=80°,则∠1+∠3的度数为______________.
答案:100°
10.如图6,直线AB、CD相交于点O,OE平分∠BOD,若∠3:∠2=8:1,求∠AOC的度数.
解:∵OE平分∠BOD ∴∠1=∠2 又∵∠3:∠2=8:1 ,∴∠3:∠2:∠1=8:1:1,
设∠1=∠2=x,则∠3=8x,又∵∠1+∠2+∠3=180°, ∴x+x+8x=180°,∴x=180°,
∴∠AOC=∠1+∠2=36°
11.(2018武汉十一初)如图7,直线AB,CD相交于点O,OE平分∠BOD,若∠3:∠2=8:1,求∠AOC的度数.
解:∵OE平分∠BOD,∴∠1=∠2,又∠3:∠2=8:1,∴∠3:∠2:∠1=8:1:1,设∠1=∠2=x,
则∠3=8x,又∠1+∠2+∠3=180°,∴x+x+8x=180°,∴x=18°,∴∠AOC=∠1+∠2=36°.
B.真题检测反馈
12.如图8,直线AB、CD、EF相交于点O,则∠BOE的对顶角是________,∠COF的邻补角是__________;若∠AOC:∠AOE=2:3,∠EOD=130°,则∠BOC=_________.
答案:∠AOF;∠COE;∠DOF;160°
13.如图9,已知∠AOB与∠BOE互为邻补角,且∠BOC>∠AOB,OD平分∠AOB,射线OE使∠BOE=false∠EOC,当∠DOE=72°时,则∠EOC的度数为_________.
答案:72°
14.将一张长方形纸片按如图10所示的方式折叠(射线false经过点false),BC、BD为折痕,求∠CBD的度数.
解:由题意∠ABC=∠false,∠EBD=∠false,又∵∠ABC+∠false+∠EBD+∠false=180°,
∴2∠false+2∠false=180°,∴∠CBD=∠false+∠false=90°
C.创新拓展提升
15.(1)两条直线相交于一点有_____组不同的对顶角;(2)三条直线相交于一点有_____组不同的对顶角;(3)四条直线相交于一点有_______组不同的对顶角;(4)n条直线相交于一点有________组不同的对顶角.
答案: 2; 6; 12; n(n-1)
16.一条直线最多将平面分成两部分,两条直线最多将平面分成4部分,三条直线最多将平面分成7部分,四条直线最多将平面分成_____部分,...,则8条直线最多将平面分成______部分.
答案:11;37
A.双基导学导练
知识点1 邻补角的定义及其性质
1.两个角有一条__________,它们的另一条边互为_________,具有这种关系的__________,________邻补角.
2.邻补角与补角的主要区别是:补角只反映两个角之间的数量关系,即__________________;而邻补角是补角的特殊情况,邻补角既有数量关系:_________________,又要有位置关系:_________________________.
3.如图1,直线AB、CD交于点O,射线OM平分∠AOC,若∠AOM=42°,则∠BOC的度数为______.
4.如图2,已知直线AB、CD交于点O,且OE平分∠BOC.
(1)直接写出∠AOC的邻补角;(2)写出∠EOA的补角,并说明理由;
(3)若∠AOC=42°,求∠BOE的度数.
知识点2 对顶角的定义及其性质
5.下列说法:①有公共顶点,没有公共边的两个角是对顶角;②相等的两个角是对顶角;③如果两个角是对顶角,那么这两个角相等;④如果一个角的两边分别是另一个角两边的反向延长线,那么这两个角是对顶角.其中正确的个数为( )
A.1 B.2 C.3 D.4
6.在下面四个图形中,∠1与∠2是对顶角的是( )
24028407683522796599695A. B.
2361565501652374901905C. D.
7.图3中是对顶量角器,它测量角的原理是__________________.
8.如图4,直线a、b、c两两相交,∠1=2∠3,∠2=64°,求∠4的度数.
知识点3 邻补角,对顶角性质的运用
9.如图5,直线AB、CD、EF都经过点O,若∠2=80°,则∠1+∠3的度数为______________.
10.如图6,直线AB、CD相交于点O,OE平分∠BOD,若∠3:∠2=8:1,求∠AOC的度数.
11.(2018武汉十一初)如图7,直线AB,CD相交于点O,OE平分∠BOD,若∠3:∠2=8:1,求∠AOC的度数.
B.真题检测反馈
12.如图8,直线AB、CD、EF相交于点O,则∠BOE的对顶角是________,∠COF的邻补角是__________;若∠AOC:∠AOE=2:3,∠EOD=130°,则∠BOC=_________.
13.如图9,已知∠AOB与∠BOE互为邻补角,且∠BOC>∠AOB,OD平分∠AOB,射线OE使∠BOE=false∠EOC,当∠DOE=72°时,则∠EOC的度数为_________.
14.将一张长方形纸片按如图10所示的方式折叠(射线false经过点false),BC、BD为折痕,求∠CBD的度数.
C.创新拓展提升
15.(1)两条直线相交于一点有_____组不同的对顶角;(2)三条直线相交于一点有_____组不同的对顶角;(3)四条直线相交于一点有_______组不同的对顶角;(4)n条直线相交于一点有________组不同的对顶角.
16.一条直线最多将平面分成两部分,两条直线最多将平面分成4部分,三条直线最多将平面分成7部分,四条直线最多将平面分成_____部分,...,则8条直线最多将平面分成______部分.
5.1.1 相交线
A.双基导学导练
知识点1 邻补角的定义及其性质
1.两个角有一条__________,它们的另一条边互为_________,具有这种关系的__________,________邻补角.
答案:公共边;反向延长线;两个角;互为
2.邻补角与补角的主要区别是:补角只反映两个角之间的数量关系,即__________________;而邻补角是补角的特殊情况,邻补角既有数量关系:_________________,又要有位置关系:_________________________.
答案:两角之和等于180度;两角之和等于180度;两角有公共的顶点和公共的边且另一半互为反向延长线
3.如图1,直线AB、CD交于点O,射线OM平分∠AOC,若∠AOM=42°,则∠BOC的度数为______.
答案:96°
4.如图2,已知直线AB、CD交于点O,且OE平分∠BOC.
(1)直接写出∠AOC的邻补角;(2)写出∠EOA的补角,并说明理由;
(3)若∠AOC=42°,求∠BOE的度数.
解:(1)∠AOC的邻补角是∠AOD,∠COB
(2)∵∠AOE+∠EOB=180° ∴∠EOA与∠EOB互补
又∵∠EOB=∠COE ∴∠AOE+∠COE=180° ∴∠AOE与∠COE也互补
(3)∵∠AOC+∠BOC=180° ∴∠BOC=180°-∠AOC=180°-42°=138°
又∵OE平分∠COB ∴∠BOE=false∠COB=69°
知识点2 对顶角的定义及其性质
5.下列说法:①有公共顶点,没有公共边的两个角是对顶角;②相等的两个角是对顶角;③如果两个角是对顶角,那么这两个角相等;④如果一个角的两边分别是另一个角两边的反向延长线,那么这两个角是对顶角.其中正确的个数为( )
A.1 B.2 C.3 D.4
答案:B
6.在下面四个图形中,∠1与∠2是对顶角的是( )
262128083185167640146050A. B.
231140272415
260540510160C. D.
答案:C
7.图3中是对顶量角器,它测量角的原理是__________________.
答案:对顶角相等
8.如图4,直线a、b、c两两相交,∠1=2∠3,∠2=64°,求∠4的度数.
解:∵∠2=65°,∴∠1=∠2=64°,又∵∠1=2∠3 ,∴∠3=false∠1=false×64°=32°,∴∠4=∠3=32°
知识点3 邻补角,对顶角性质的运用
9.如图5,直线AB、CD、EF都经过点O,若∠2=80°,则∠1+∠3的度数为______________.
答案:100°
10.如图6,直线AB、CD相交于点O,OE平分∠BOD,若∠3:∠2=8:1,求∠AOC的度数.
解:∵OE平分∠BOD ∴∠1=∠2 又∵∠3:∠2=8:1 ,∴∠3:∠2:∠1=8:1:1,
设∠1=∠2=x,则∠3=8x,又∵∠1+∠2+∠3=180°, ∴x+x+8x=180°,∴x=180°,
∴∠AOC=∠1+∠2=36°
11.(2018武汉十一初)如图7,直线AB,CD相交于点O,OE平分∠BOD,若∠3:∠2=8:1,求∠AOC的度数.
解:∵OE平分∠BOD,∴∠1=∠2,又∠3:∠2=8:1,∴∠3:∠2:∠1=8:1:1,设∠1=∠2=x,
则∠3=8x,又∠1+∠2+∠3=180°,∴x+x+8x=180°,∴x=18°,∴∠AOC=∠1+∠2=36°.
B.真题检测反馈
12.如图8,直线AB、CD、EF相交于点O,则∠BOE的对顶角是________,∠COF的邻补角是__________;若∠AOC:∠AOE=2:3,∠EOD=130°,则∠BOC=_________.
答案:∠AOF;∠COE;∠DOF;160°
13.如图9,已知∠AOB与∠BOE互为邻补角,且∠BOC>∠AOB,OD平分∠AOB,射线OE使∠BOE=false∠EOC,当∠DOE=72°时,则∠EOC的度数为_________.
答案:72°
14.将一张长方形纸片按如图10所示的方式折叠(射线false经过点false),BC、BD为折痕,求∠CBD的度数.
解:由题意∠ABC=∠false,∠EBD=∠false,又∵∠ABC+∠false+∠EBD+∠false=180°,
∴2∠false+2∠false=180°,∴∠CBD=∠false+∠false=90°
C.创新拓展提升
15.(1)两条直线相交于一点有_____组不同的对顶角;(2)三条直线相交于一点有_____组不同的对顶角;(3)四条直线相交于一点有_______组不同的对顶角;(4)n条直线相交于一点有________组不同的对顶角.
答案: 2; 6; 12; n(n-1)
16.一条直线最多将平面分成两部分,两条直线最多将平面分成4部分,三条直线最多将平面分成7部分,四条直线最多将平面分成_____部分,...,则8条直线最多将平面分成______部分.
答案:11;37
