二次根式复习教案

教 案 授课人：孟宪静
第 2周 第 8 节 主备人 穆桂青 2012 年2 月 2 4日
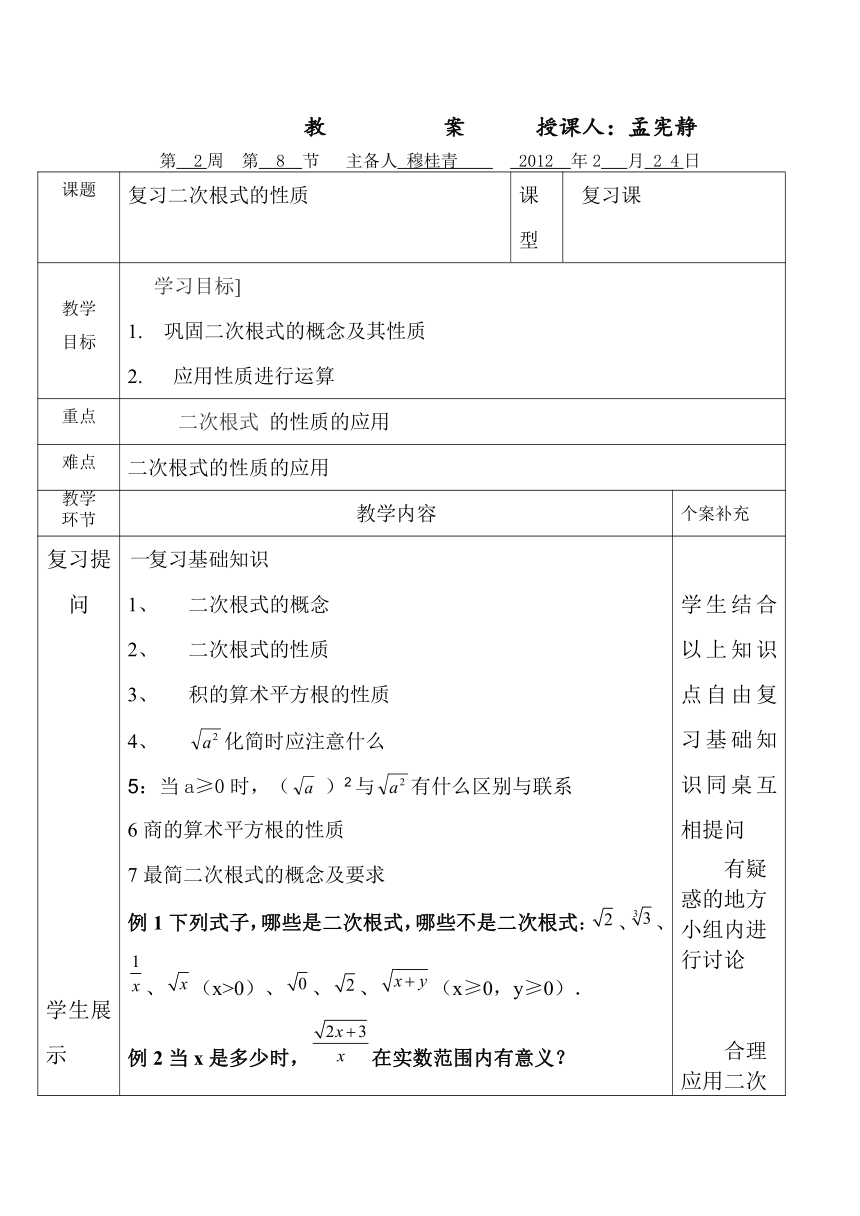
课题 复习二次根式的性质 课型 复习课
教学目标 学习目标] 巩固二次根式的概念及其性质2. 应用性质进行运算
重点 二次根式 的性质的应用
难点 二次根式的性质的应用
教学环节 教学内容 个案补充
复习提问学生展示合作交流 一复习基础知识二次根式的概念二次根式的性质积的算术平方根的性质 化简时应注意什么5：当a≥0时，（ ）2与有什么区别与联系6商的算术平方根的性质 7最简二次根式的概念及要求例1下列式子，哪些是二次根式，哪些不是二次根式：、、、（x>0）、、、（x≥0，y≥0）．例2当x是多少时，在实数范围内有意义？例3、化简 （1） （2） (3)例4 化简：(1) (2)（3） (4) (5) 练习一、填空题：1．像，（b≥3），（s≥0），这种形如（）的代数式，叫做_______．2．当x______ 时，有意义． 3．如果是二次根式，则x的取值范围是_______ ．4．（7）（）2-=________；（8）+（-）2=________．（10）+=_______．5．当x=-2时，二次根式的值为_______． 6．当a取______时，有意义．7．当x取______时，有意义． 8．当m=-2时，二次根式的值为________．9、若直角三角形的两直角边分别是2cm 和acm，则直角三角形的斜边长是_______10、若正方形的面积是（b-3）cm2,则正方形的边长是_________。二、选择题：1．下列各式中，哪一个是二次根式 （ ）A． B． C． D．2．使代数式有意义的x的取值范围是（ ） A．x≠-2; B．x≤且x≠-2; C．x<且x≠-2; D．x≥且x≠-23．下列各式中一定成立的是（ ）A．=+=3+4=7 B．=- C．（-）2= D．=1-=三、求下列二次根式中字母的取值范围：四、计算：（1）--（）2; （2） + （3） 四、小结：本节课复习了二次根式概念、性质，要求同学们会熟练进行二次根式性质进行化简，并会对结果进行化简处理。 学生结合以上知识点自由复习基础知识同桌互相提问有疑惑的地方小组内进行讨论合理应用二次根式的性质，可以帮助我们简化实数的运算。教师提问，教师板书解题过程进行教学。二次根式化简是，将根号内的平方数开方，从而对二次根式进行化简. 学生独立完成练习教师出示答案
板书设计 二次根式(复习课) 例3 例2 例4
教后反思 先复习后练习，有利于培养学生的学习习惯,增强学生学数学的信念。