六年级数学下册课件-6.4正反比例的复习苏教版(共17张PPT)
文档属性
| 名称 | 六年级数学下册课件-6.4正反比例的复习苏教版(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 461.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
江苏国标版小学数学六年级下册
确定位置
江阴市实验小学
钱燕芳
正反比例的复习
自主复习
问题1:什么是正比例关系?什么是反比例关
系?我们怎样判断两种量是否成正比例或反比例关系?
问题2:举出一个生活中成正比例或反比例的
量的例子。
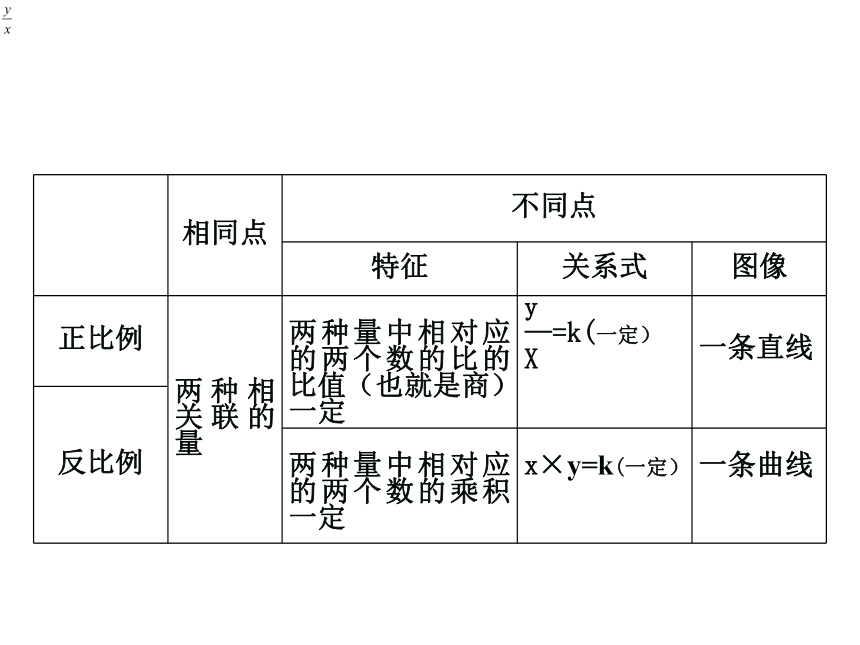
问题3:比较一下,正比例和反比例有什么相同点和不同点?
相同点
不同点
特征
关系式
图像
正比例
两种相关联的量
两种量中相对应的两个数的比的比值(也就是商)一定
y
—=k(一定)
X
一条直线
反比例
两种量中相对应的两个数的乘积一定
x×y=k(一定)
一条曲线
都是研究两个变量之间的关系。
在变化中都蕴含着不变的规律。
0
2
3
4
5
6
7
1
240
40
80
120
160
200
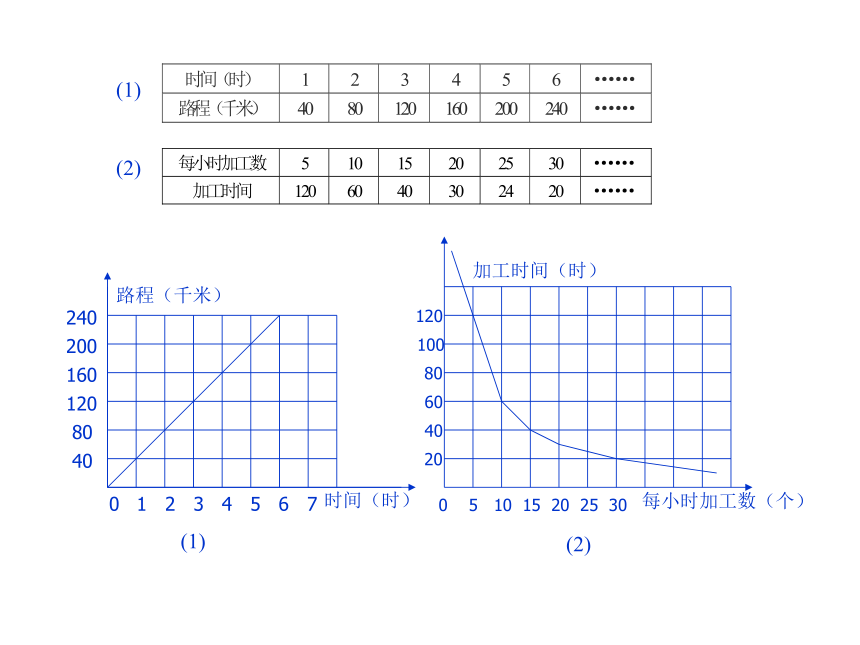
路程(千米)
(1)
(1)
0
5
10
15
20
25
30
120
20
40
60
80
100
加工时间(时)
(2)
(2)
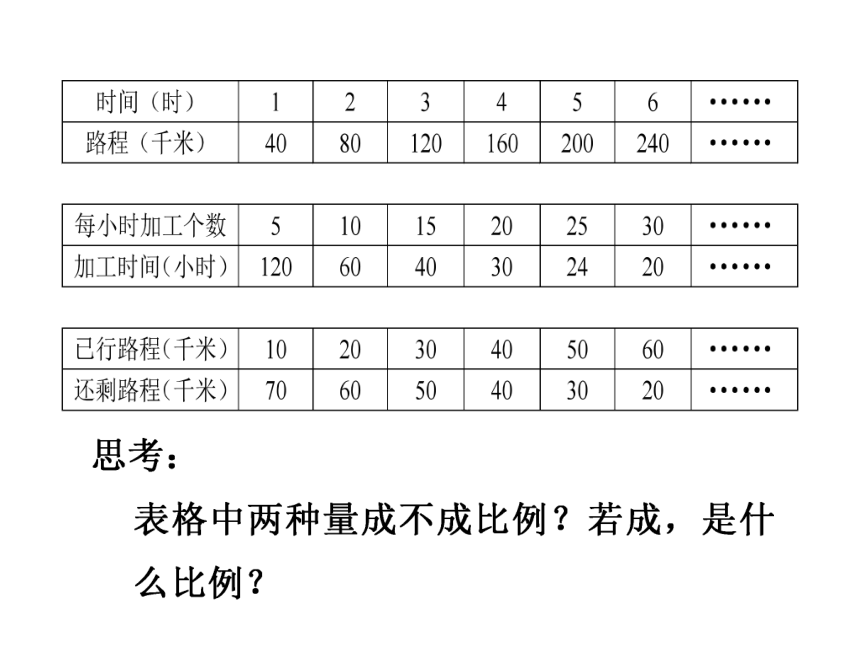
时间(时)
每小时加工数(个)
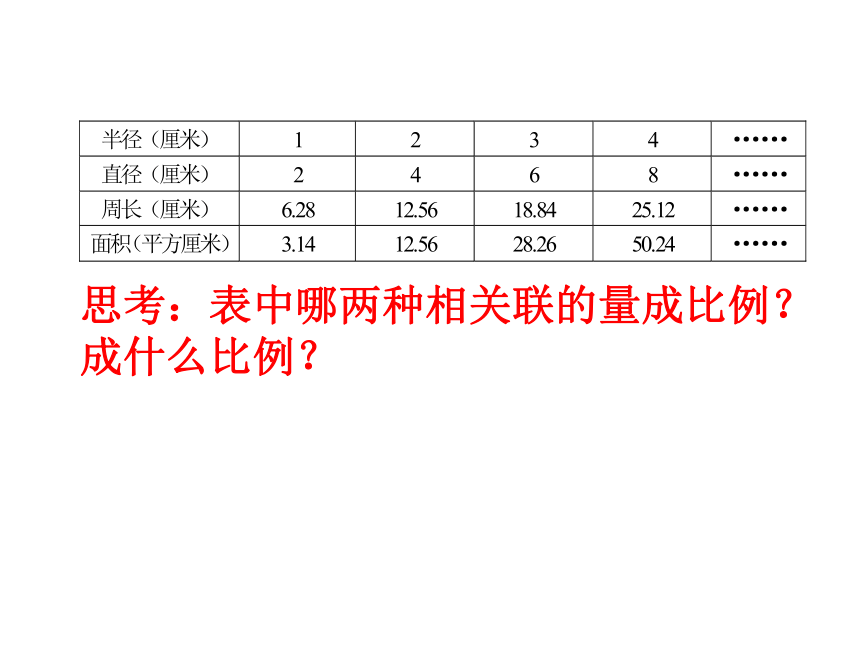
思考:表中哪两种相关联的量成比例?成什么比例?
题组比较:下面两种量成什么比例?
第一组:
1)???小李一天工作8小时,每小时加工零件数和零件总数
2)???小李一天工作8小时,加工一个零件所用的时间和零件总数
零件总数
每小时加工零件数
=8小时(一定)
加工一个零件所用的时间
×零件总数=8小时(一定)
第二组:
(1)铺地面积一定,每块方砖的面积和所需块数
(
)
(2)铺地面积一定,每块方砖的边长和所需块数
(
)
第三组:
(1)车轮的周长一定,所行驶的路程和车轮的转数。(
)
(2)车轮的直径一定,所行驶的路程和车轮的转数。(
)
第四组:
(1)
长方形的周长一定,长和宽
(
)
(2)长方形的面积一定,长和宽
(
)
一式多变:
(1)
如果A×B=C,那么:
C一定,A和B成(
)比例
B一定,A和C成(
)比例
A一定,B和C成(
)比例
例:底面积×高=圆柱体积
—
(2)如果A÷B=C,那么:
C一定,A和B成(
)比例
B一定,A和C成(
)比例
A一定,B和C成(
)比例
例:
快速判断两种量成不成比例?成什么比例?
1)?圆锥的体积一定,它的底面积和高
2)?一个圆的周长与圆周率
3)?分子一定,分母和分数值
4)小麦的出粉率一定,小麦的重量与面粉的重量
.
用正反比例解决实际问题
(1)小明身高1.5米,在下午4点的校园里,测得小明的影子长0.6米,一棵大树的影子长2米,这棵大树高多少米?
(2)一批煤,计划每天烧6吨,可以烧80天,实际每天烧8吨,这批煤可以烧多少天?
(3)一种农药,用药液和水按1:1500配制而成。现有3千克药液,能配制这种农药多少千克?
(4)一间房子用方砖铺地,用边长3分米的方砖,需要96块。如改用边长2分米的方砖,那么需要多少块?
江苏国标版小学数学六年级下册
确定位置
江阴市实验小学
钱燕芳
正反比例的复习
自主复习
问题1:什么是正比例关系?什么是反比例关
系?我们怎样判断两种量是否成正比例或反比例关系?
问题2:举出一个生活中成正比例或反比例的
量的例子。
问题3:比较一下,正比例和反比例有什么相同点和不同点?
相同点
不同点
特征
关系式
图像
正比例
两种相关联的量
两种量中相对应的两个数的比的比值(也就是商)一定
y
—=k(一定)
X
一条直线
反比例
两种量中相对应的两个数的乘积一定
x×y=k(一定)
一条曲线
都是研究两个变量之间的关系。
在变化中都蕴含着不变的规律。
0
2
3
4
5
6
7
1
240
40
80
120
160
200
路程(千米)
(1)
(1)
0
5
10
15
20
25
30
120
20
40
60
80
100
加工时间(时)
(2)
(2)
时间(时)
每小时加工数(个)
思考:表中哪两种相关联的量成比例?成什么比例?
题组比较:下面两种量成什么比例?
第一组:
1)???小李一天工作8小时,每小时加工零件数和零件总数
2)???小李一天工作8小时,加工一个零件所用的时间和零件总数
零件总数
每小时加工零件数
=8小时(一定)
加工一个零件所用的时间
×零件总数=8小时(一定)
第二组:
(1)铺地面积一定,每块方砖的面积和所需块数
(
)
(2)铺地面积一定,每块方砖的边长和所需块数
(
)
第三组:
(1)车轮的周长一定,所行驶的路程和车轮的转数。(
)
(2)车轮的直径一定,所行驶的路程和车轮的转数。(
)
第四组:
(1)
长方形的周长一定,长和宽
(
)
(2)长方形的面积一定,长和宽
(
)
一式多变:
(1)
如果A×B=C,那么:
C一定,A和B成(
)比例
B一定,A和C成(
)比例
A一定,B和C成(
)比例
例:底面积×高=圆柱体积
—
(2)如果A÷B=C,那么:
C一定,A和B成(
)比例
B一定,A和C成(
)比例
A一定,B和C成(
)比例
例:
快速判断两种量成不成比例?成什么比例?
1)?圆锥的体积一定,它的底面积和高
2)?一个圆的周长与圆周率
3)?分子一定,分母和分数值
4)小麦的出粉率一定,小麦的重量与面粉的重量
.
用正反比例解决实际问题
(1)小明身高1.5米,在下午4点的校园里,测得小明的影子长0.6米,一棵大树的影子长2米,这棵大树高多少米?
(2)一批煤,计划每天烧6吨,可以烧80天,实际每天烧8吨,这批煤可以烧多少天?
(3)一种农药,用药液和水按1:1500配制而成。现有3千克药液,能配制这种农药多少千克?
(4)一间房子用方砖铺地,用边长3分米的方砖,需要96块。如改用边长2分米的方砖,那么需要多少块?
