七年级数学三角形
图片预览



文档简介
(共14张PPT)
第七章 三角形
复 习
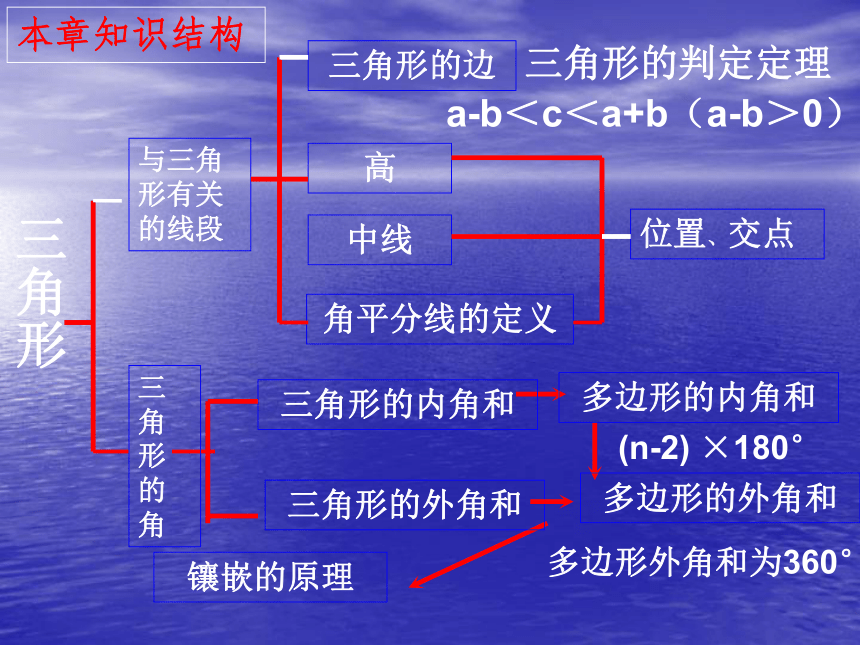
(n-2) ×180°
三角形
与三角形有关的线段
a-b<c<a+b(a-b>0)
高
三角形的边
三角形的判定定理
中线
角平分线的定义
位置、交点
三角形的内角和
多边形的内角和
多边形的外角和
三角形的外角和
多边形外角和为360°
镶嵌的原理
本章知识结构
三角形的角
1、记住以下角度:
(1)三角形的内角和为______;
180°
四边形的内角和为______;
360°
五边形的内角和为______;
540°
六边形的内角和为______;
720°
(2)正三角形的每个内角为______;
60°
正四边形的每个内角为______;
90°
正五边形的每个内角为______;
108°
正六边形的每个内角为______;
120°
1.下列条件中能组成三角形的是( ) A、5cm,7cm,13cm B、3cm,5cm,9cm C、6cm,9cm,14cm D、5cm,6cm,11cm
C
2.三角形的两边为7cm和5cm,则
第三边x的范围是 ;
2cm<X <12cm
基础过关
那么周长C的范围呢?
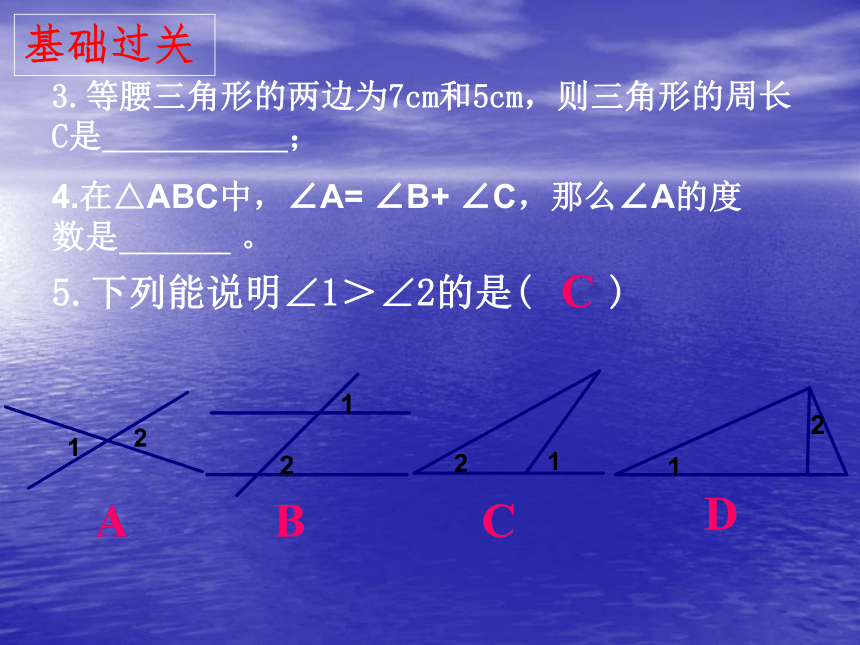
3.等腰三角形的两边为7cm和5cm,则三角形的周长C是 ;
4.在△ABC中,∠A= ∠B+ ∠C,那么∠A的度数是 。
5.下列能说明∠1>∠2的是( )
A
B
D
C
C
基础过关
C
A
B
D
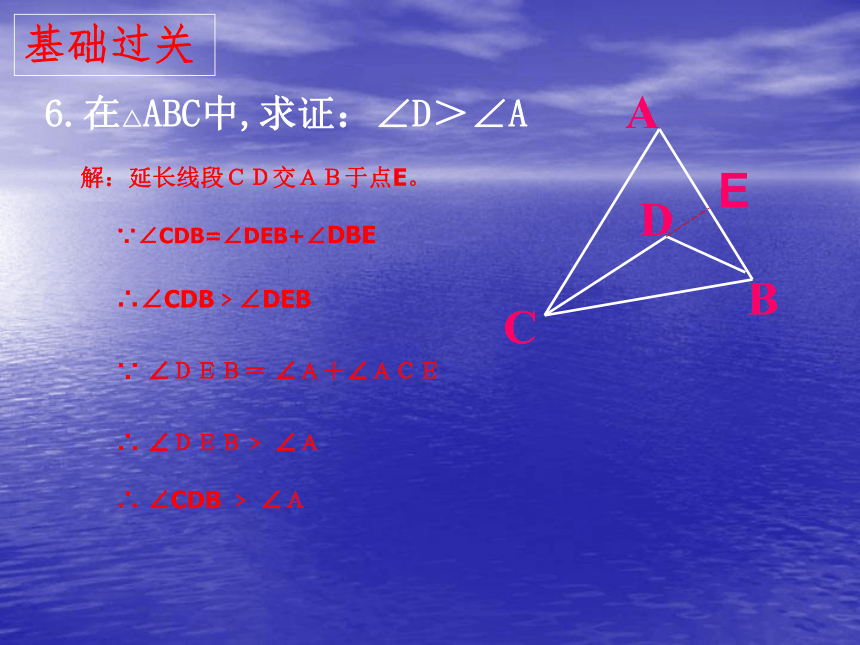
6.在△ABC中,求证:∠D>∠A
E
基础过关
解:延长线段CD交AB于点E。
∵∠CDB=∠DEB+∠DBE
∴∠CDB﹥∠DEB
∵ ∠DEB= ∠A+∠ACE
∴ ∠DEB﹥ ∠A
∴ ∠CDB ﹥ ∠A
7. ①如图, ∠A+∠B+∠C+∠D+∠E+∠F= ;
360°
基础过关
②如图,求∠A+∠B+∠C+∠ADC+∠AEB的度数。
D
A
B
C
E
A
B
C
D
E
F
G
H
③如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
8.如图, 在△ABC中, BD、CE分别平分∠ABC和∠ACB.
(1).若∠A=60°,求∠BOC的度数.
(2).若∠A=α,求∠BOC的度数.
如果BD、CE分别平分
∠ABC和
∠ACB的外角呢?
9.如图, 在△ABC中, 延长BC至D, BE、CE分别平分∠ABC和∠ACD.
(1).若∠A=80°,求∠E的度数.
(2).根据(1)猜测∠E 与∠A的关系,并说明理由.
数学思想: 整体思想和转化思想
在一个图形中同时出现两条角平分线时,常常要用到整体思想.
运用转化思想将复杂的问题转化为简单的问题,将未知的问题转化为已知的问题,是常用的数学方法.
1.如图,直线DE与△ABC的三边所在直线交与D、E、F, ∠A=40°,D=25°,DE⊥AB,求ACB的度数.
课后作业
2.若一个三角形的三个外角度数之比为3:4:5,则与之相邻的三个内角度数之比为( )
A.3:4:5 B. 1:2:3
C. 5:4:3 D. 3:2:1
3.(06,湖南)如图,若AB∥CD,EF与AB、CD分别相交于E、 F,PE⊥EF, ∠EFD的平分线与EP交于P,且∠BEP=40°,则∠EPF= ;
65°
综合训练
第七章 三角形
复 习
(n-2) ×180°
三角形
与三角形有关的线段
a-b<c<a+b(a-b>0)
高
三角形的边
三角形的判定定理
中线
角平分线的定义
位置、交点
三角形的内角和
多边形的内角和
多边形的外角和
三角形的外角和
多边形外角和为360°
镶嵌的原理
本章知识结构
三角形的角
1、记住以下角度:
(1)三角形的内角和为______;
180°
四边形的内角和为______;
360°
五边形的内角和为______;
540°
六边形的内角和为______;
720°
(2)正三角形的每个内角为______;
60°
正四边形的每个内角为______;
90°
正五边形的每个内角为______;
108°
正六边形的每个内角为______;
120°
1.下列条件中能组成三角形的是( ) A、5cm,7cm,13cm B、3cm,5cm,9cm C、6cm,9cm,14cm D、5cm,6cm,11cm
C
2.三角形的两边为7cm和5cm,则
第三边x的范围是 ;
2cm<X <12cm
基础过关
那么周长C的范围呢?
3.等腰三角形的两边为7cm和5cm,则三角形的周长C是 ;
4.在△ABC中,∠A= ∠B+ ∠C,那么∠A的度数是 。
5.下列能说明∠1>∠2的是( )
A
B
D
C
C
基础过关
C
A
B
D
6.在△ABC中,求证:∠D>∠A
E
基础过关
解:延长线段CD交AB于点E。
∵∠CDB=∠DEB+∠DBE
∴∠CDB﹥∠DEB
∵ ∠DEB= ∠A+∠ACE
∴ ∠DEB﹥ ∠A
∴ ∠CDB ﹥ ∠A
7. ①如图, ∠A+∠B+∠C+∠D+∠E+∠F= ;
360°
基础过关
②如图,求∠A+∠B+∠C+∠ADC+∠AEB的度数。
D
A
B
C
E
A
B
C
D
E
F
G
H
③如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
8.如图, 在△ABC中, BD、CE分别平分∠ABC和∠ACB.
(1).若∠A=60°,求∠BOC的度数.
(2).若∠A=α,求∠BOC的度数.
如果BD、CE分别平分
∠ABC和
∠ACB的外角呢?
9.如图, 在△ABC中, 延长BC至D, BE、CE分别平分∠ABC和∠ACD.
(1).若∠A=80°,求∠E的度数.
(2).根据(1)猜测∠E 与∠A的关系,并说明理由.
数学思想: 整体思想和转化思想
在一个图形中同时出现两条角平分线时,常常要用到整体思想.
运用转化思想将复杂的问题转化为简单的问题,将未知的问题转化为已知的问题,是常用的数学方法.
1.如图,直线DE与△ABC的三边所在直线交与D、E、F, ∠A=40°,D=25°,DE⊥AB,求ACB的度数.
课后作业
2.若一个三角形的三个外角度数之比为3:4:5,则与之相邻的三个内角度数之比为( )
A.3:4:5 B. 1:2:3
C. 5:4:3 D. 3:2:1
3.(06,湖南)如图,若AB∥CD,EF与AB、CD分别相交于E、 F,PE⊥EF, ∠EFD的平分线与EP交于P,且∠BEP=40°,则∠EPF= ;
65°
综合训练
