6.3 向心加速度(强化提高)学案— 2020-2021学年【新教材】人教版(2019)高中物理必修第二册word版含答案
文档属性
| 名称 | 6.3 向心加速度(强化提高)学案— 2020-2021学年【新教材】人教版(2019)高中物理必修第二册word版含答案 | 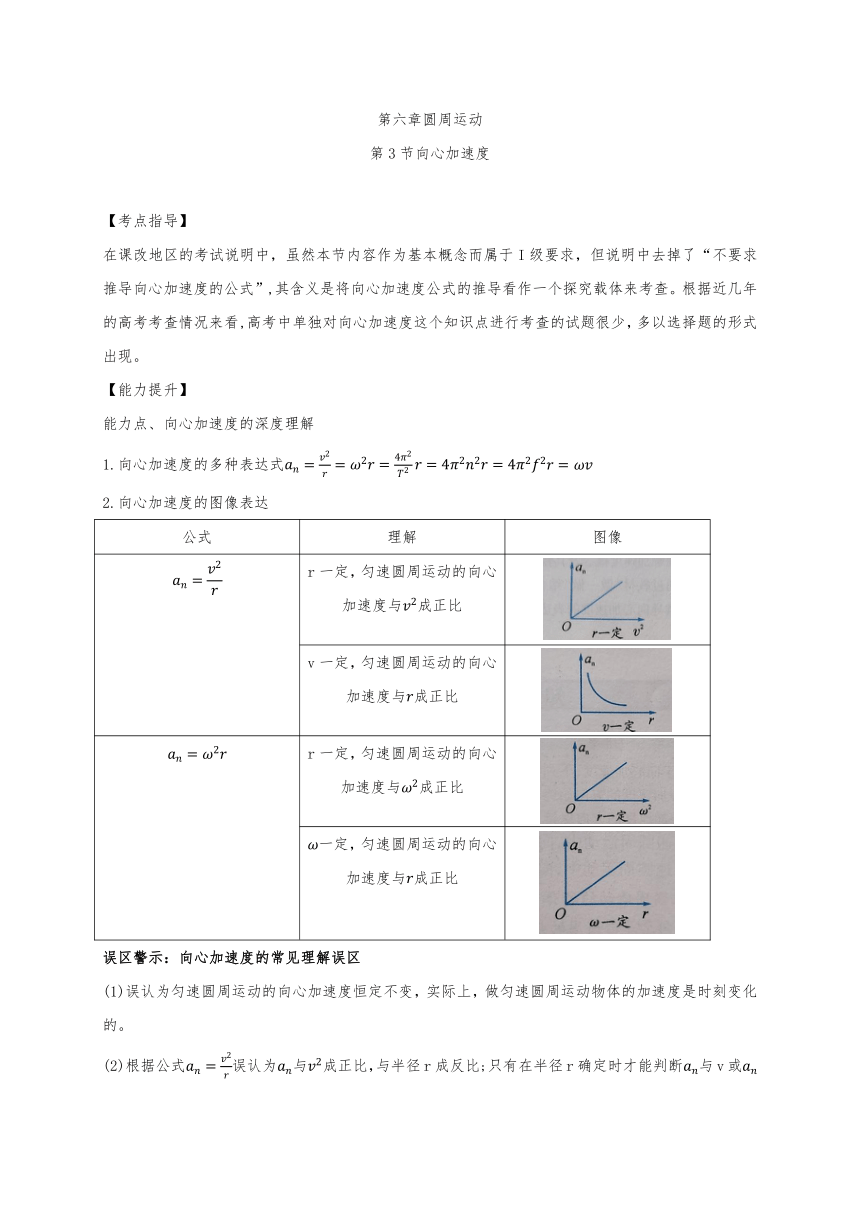 | |
| 格式 | docx | ||
| 文件大小 | 227.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-21 22:52:08 | ||
图片预览



文档简介
第六章圆周运动
第3节向心加速度
【考点指导】
在课改地区的考试说明中,虽然本节内容作为基本概念而属于I级要求,但说明中去掉了“不要求推导向心加速度的公式”,其含义是将向心加速度公式的推导看作一个探究载体来考查。根据近几年的高考考查情况来看,高考中单独对向心加速度这个知识点进行考查的试题很少,多以选择题的形式出现。
【能力提升】
能力点、向心加速度的深度理解
1.向心加速度的多种表达式an=v2r=ω2r=4π2T2r=4π2n2r=4π2f2r=ωv
2.向心加速度的图像表达
公式
理解
图像
an=v2r
r一定,匀速圆周运动的向心加速度与v2成正比
v一定,匀速圆周运动的向心加速度与r成正比
an=ω2r
r一定,匀速圆周运动的向心加速度与ω2成正比
ω一定,匀速圆周运动的向心加速度与r成正比
误区警示:向心加速度的常见理解误区
(1)误认为匀速圆周运动的向心加速度恒定不变,实际上,做匀速圆周运动物体的加速度是时刻变化的。
(2)根据公式an=v2r误认为an与v2成正比,与半径r成反比;只有在半径r确定时才能判断an与v或an与ω的关系。
(3)误认为做圆周运动物体的加速度一定指向圆心。只有做匀速圆周运动的物体其加速度才指向圆心,做变速圆周运动的物体一般具有切向加速度,所以加速度一般不指向圆心。
名师指导:
加速度是指合加速度,反映速度变化的快慢,在匀速圆周运动中,速度的大小不变,那么向心加速度等于合加速度,是反映速度方向变化快慢的物理量,向心加速度的大小不变,但方向时刻改变,是变化的加速度;在变速圆周运动中,加速度不指向圆心,加速度可以分解为向心加速度和沿切线方向的切向加速度,向心加速度反映线速度方向的变化快慢,而切向加速度则反映线速度大小的变化快慢。
名师指导
加速度发生突变的两种情况
(1)物体由曲面进入平面的瞬间,加速度的大小可能由某值突变为0。
(2)两个不同半径的曲面平滑相连,在连接点处的加速度发生突变。
[注意]速度大小不能发生突变,但加速度可以发生突变。
【典型例题】
1.甲、乙两名溜冰运动员,M甲=80kg,M乙=40kg,面对面拉着弹簧秤做圆周运动的溜冰表演,如图所示,两人相距0.9m,弹簧秤的示数为9.2N,下列判断中正确的是( )
A.两人的线速度相同,约为40m/s
B.两人的角速度相同,为6rad/s
C.两人的运动半径相同,都是0.45m
D.两人的运动半径不同,甲为0.3m,乙为0.6m
【答案】D
【详解】
两名运动员绕同一点转动,所以角速度相等,根据线速度与角速度的关系
可知两人的线速度不相同;他们做圆周运动的向心力是由弹簧弹力提供的,所以向心力也相等,由
又由
r甲+r乙=0.9 m
联立得r甲=0.3 m,r乙=0.6 m;半径大小代回向心力公式可得ω=0.6 rad/s。
故选D。
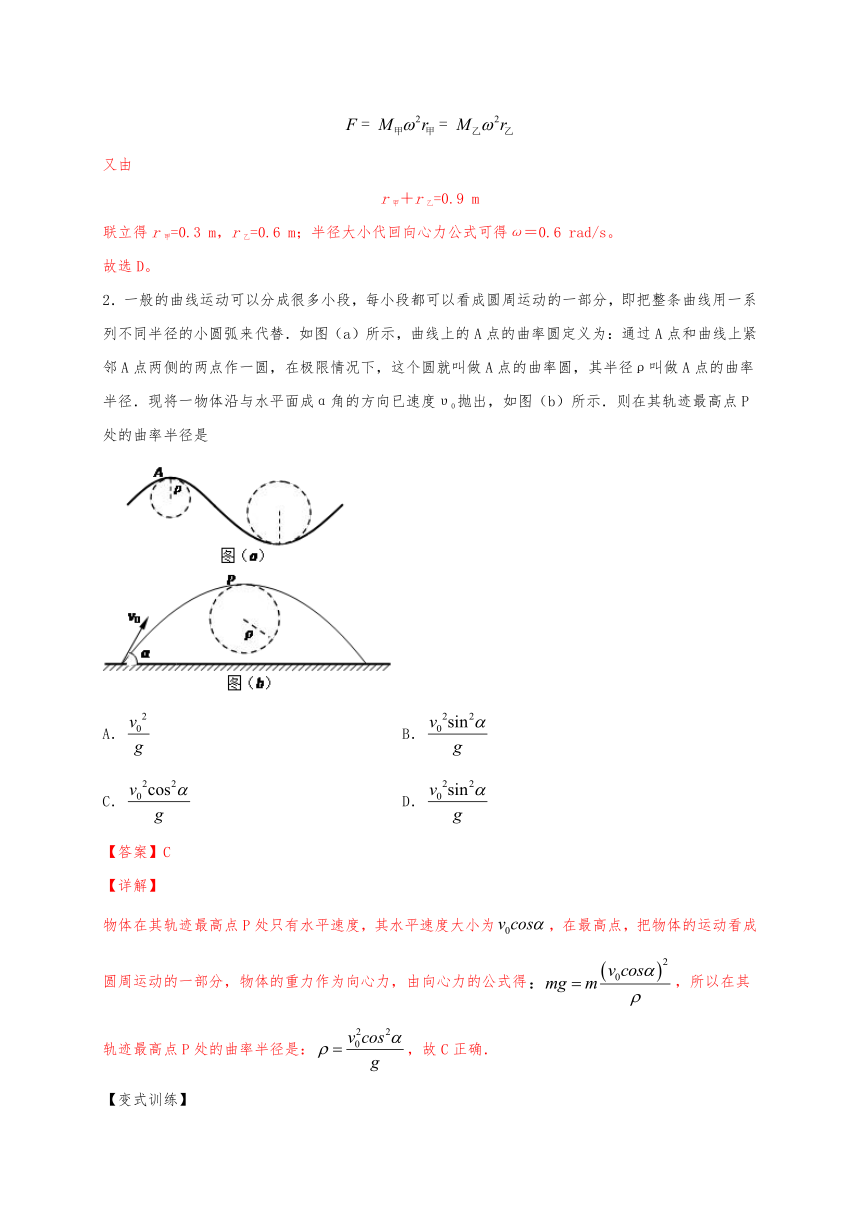
2.一般的曲线运动可以分成很多小段,每小段都可以看成圆周运动的一部分,即把整条曲线用一系列不同半径的小圆弧来代替.如图(a)所示,曲线上的A点的曲率圆定义为:通过A点和曲线上紧邻A点两侧的两点作一圆,在极限情况下,这个圆就叫做A点的曲率圆,其半径ρ叫做A点的曲率半径.现将一物体沿与水平面成α角的方向已速度υ0抛出,如图(b)所示.则在其轨迹最高点P处的曲率半径是
A. B.
C. D.
【答案】C
【详解】
物体在其轨迹最高点P处只有水平速度,其水平速度大小为,在最高点,把物体的运动看成圆周运动的一部分,物体的重力作为向心力,由向心力的公式得,所以在其轨迹最高点P处的曲率半径是:,故C正确.
【变式训练】
1.下列说法正确的是( )
A.做曲线运动的物体的速度大小一定变化
B.做曲线运动的物体一定有合外力,一定有加速度
C.平抛运动是变加速曲线运动
D.匀速圆周运动的向心力、向心加速度不变
【答案】B
【解析】A.做曲线运动的物体的速度大小不一定变化,但方向时刻改变,所以A错误;
B.做曲线运动的物体一定有合外力,一定有加速度,所以B正确;
C.平抛运动只受重力作用,所以是匀变速曲线运动,则C错误;
D.匀速圆周运动的向心力、向心加速度大小不变,但是方向时刻改变,所以D错误;
故选B。
2.A、B两物体在水平面上做匀速圆周运动。在相同时间内,它们通过的路程之比是4︰3,运动方向改变的角度之比是3︰2,则两物体做匀速圆周运动的( )
A.半径之比为2︰1 B.角速度大小之比为3︰4
C.线速度大小之比为4︰3 D.向心加速度大小之比为1︰2
【答案】C
【解析】ABC.因A、B时间相等内通过的路程之比为4︰3,根据线速度
则线速度之比为4︰3;
因运动方向改变的角度等于圆周运动转过的角度,A、B转过的角度之比为3︰2,时间相等,根据角速度
则角速度大小之比为3︰2;
根据
得圆周运动的半径,线速度之比为4︰3,角速度之比为3︰2,则圆周运动的半径之比为8︰9,故AB错误,C正确;
D.根据
得,线速度之比为4︰3,角速度之比为3︰2,则向心加速度之比为2︰1,故D错误。
故选C。
3.如图所示,皮带传动装置右轮的半径为r,a是它边缘上的一点;左侧为一轮轴,大轮的半径为4r,小轮的半径为2r,b点在小轮上,到小轮中心的距离为r,c点和d点分别位于小轮和大轮的边缘上。若在传动过程中,皮带不打滑,则( )
A.a点与b点的线速度大小相等
B.b点与d点的角速度大小不等
C.a点与d点的向心加速度大小相等
D.a、b、c、d四点中,向心加速度最小的是c点
【答案】C
【解析】A.由题意可得,a、c线速度大小相等, b、c角速度相等,由于,由
可得:,A错误;
B.由于b、d两点共轴转动,因此,B错误;
C.由题意可得,a、c线速度大小相等,由
可得:;
d、c角速度相等,由
可得:;
故a点与d点的向心加速度大小相等,C正确;
D.a点与d点的向心加速度大小相等,b、c、d角速度相等,根据
可得:向心加速度最小的是b点,D错误;
故选C。
4.如图所示,长为L的轻杆,一端固定有一个质量为m的可视为质点的小球,另一端固定在水平转轴O上,杆随转轴O在竖直平面内匀速转动,角速度为ω,某时刻杆对球的作用力为F,方向恰好与杆垂直,此时杆与水平面的夹角为θ.则下列关系正确的是
A.tanθ=g/(ω2L) B.sinθ=ω2L/g C.θ=0 D.F=mg/cosθ
【答案】B
【解析】小球所受重力和杆子的作用力的合力提供向心力,根据牛顿第二定律有,解得,故选项B正确,A、C、D错误.
5.两个质量相同的小球a、b用长度不等的细线拴在天花板上的同一点并在空中同一水平面内做匀速圆周运动,如图所示,则关于a、b两小球说法正确的是( )
A.a球角速度大于b球角速度
B.a球线速度大于b球线速度
C.a球向心力等于b球向心力
D.a球向心加速度小于b球向心加速度
【答案】B
【解析】A、对其中一个小球受力分析,如图,受重力,绳子的拉力,由于小球做匀速圆周运动,故合力提供向心力;
将重力与拉力合成,合力指向圆心,由几何关系得,合力:F=mgtanθ ①;
由向心力公式得到,F=mω2r ②;
设球与悬挂点间的高度差为h,由几何关系,得:r=htanθ ③;
由①②③三式得:,与绳子的长度和转动半径无关,与高度h有关;而两球圆周运动到悬点的高度相同,则有;故A错误;
B、因两球角速度相等,由v=wr,两球转动半径,则线速度,故B正确;
C、由F=mω2r,两球转动半径,而质量m和角速度相等,则向心力,故C错误;
D、由a=ω2r,角速度相等而转动半径,则向心加速度,故D错误;
故选B.
6.如图所示,为一皮带传动装置,右轮半径为r,a为它边缘上一点;左侧是一轮轴,大轮半径为4r,小轮半径为2r,b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若传动过程中皮带不打滑,则:( )
①a点和b点的线速度大小相等
②a点和b点的角速度大小相等
③a点和c点的线速度大小相等
④a点和d点的向心加速度大小相等
A.①③ B.②③ C.③④ D.②④
【答案】C
【解析】
a、c为共线关系,线速度相等,b、c为共轴关系,加速度相等,b、c的线速度不相等,①错;由v=wr可知,a、c的线速度相等,角速度不相等,②错;③对;设a的线速度为v,加速度为,c的线速度为v,角速度为,c、d角速度相同,d的线速度为2v,d的加速度为,④对;
7.如图所示,水平杆固定在竖直杆上,两者互相垂直,水平杆上O、A两点连接有两轻绳,两绳的另一端都系在质量为m的小球上,OA=OB=AB,现通过转动竖直杆,使水平杆在水平面内做匀速圆周运动,三角形OAB始终在竖直平面内,若转动过程中OB、AB两绳始终处于拉直状态,则下列说法正确的是( )
A.OB绳的拉力范围为0~mg
B.OB绳的拉力范围为mg~mg
C.AB绳的拉力范围为mg~mg
D.AB绳的拉力范围为0~mg
【答案】B
【解析】转动的角速度为零时,OB绳的拉力最小,AB绳的拉力最大,这时二者的值相同,设为T1,则有2T1cos30°=mg
解得T1=mg
增大转动的角速度,当AB绳的拉力刚好为零时,OB绳的拉力最大,设这时OB绳的拉力为T2,则有T2cos30°=mg
解得T2=mg
因此OB绳的拉力范围mg~mg,AB绳的拉力范围0~mg,故B正确,ACD错误。
故选B。
8.在探究向心力的大小与质量、角速度和半径之间关系的实验中,如图所示,是研究哪两个物理量之间的关系( )
A.研究向心力与质量之间的关系
B.研究向心力与角速度之间的关系
C.研究向心力与半径之间的关系
D.研究向心力与线速度之间的关系
【答案】A
【解析】铝球与钢球质量不同,转速相同,本实验研究向心力与质量之间的关系,不是研究向心力与角速度、半径、线速度的关系。
故选A。
第3节向心加速度
【考点指导】
在课改地区的考试说明中,虽然本节内容作为基本概念而属于I级要求,但说明中去掉了“不要求推导向心加速度的公式”,其含义是将向心加速度公式的推导看作一个探究载体来考查。根据近几年的高考考查情况来看,高考中单独对向心加速度这个知识点进行考查的试题很少,多以选择题的形式出现。
【能力提升】
能力点、向心加速度的深度理解
1.向心加速度的多种表达式an=v2r=ω2r=4π2T2r=4π2n2r=4π2f2r=ωv
2.向心加速度的图像表达
公式
理解
图像
an=v2r
r一定,匀速圆周运动的向心加速度与v2成正比
v一定,匀速圆周运动的向心加速度与r成正比
an=ω2r
r一定,匀速圆周运动的向心加速度与ω2成正比
ω一定,匀速圆周运动的向心加速度与r成正比
误区警示:向心加速度的常见理解误区
(1)误认为匀速圆周运动的向心加速度恒定不变,实际上,做匀速圆周运动物体的加速度是时刻变化的。
(2)根据公式an=v2r误认为an与v2成正比,与半径r成反比;只有在半径r确定时才能判断an与v或an与ω的关系。
(3)误认为做圆周运动物体的加速度一定指向圆心。只有做匀速圆周运动的物体其加速度才指向圆心,做变速圆周运动的物体一般具有切向加速度,所以加速度一般不指向圆心。
名师指导:
加速度是指合加速度,反映速度变化的快慢,在匀速圆周运动中,速度的大小不变,那么向心加速度等于合加速度,是反映速度方向变化快慢的物理量,向心加速度的大小不变,但方向时刻改变,是变化的加速度;在变速圆周运动中,加速度不指向圆心,加速度可以分解为向心加速度和沿切线方向的切向加速度,向心加速度反映线速度方向的变化快慢,而切向加速度则反映线速度大小的变化快慢。
名师指导
加速度发生突变的两种情况
(1)物体由曲面进入平面的瞬间,加速度的大小可能由某值突变为0。
(2)两个不同半径的曲面平滑相连,在连接点处的加速度发生突变。
[注意]速度大小不能发生突变,但加速度可以发生突变。
【典型例题】
1.甲、乙两名溜冰运动员,M甲=80kg,M乙=40kg,面对面拉着弹簧秤做圆周运动的溜冰表演,如图所示,两人相距0.9m,弹簧秤的示数为9.2N,下列判断中正确的是( )
A.两人的线速度相同,约为40m/s
B.两人的角速度相同,为6rad/s
C.两人的运动半径相同,都是0.45m
D.两人的运动半径不同,甲为0.3m,乙为0.6m
【答案】D
【详解】
两名运动员绕同一点转动,所以角速度相等,根据线速度与角速度的关系
可知两人的线速度不相同;他们做圆周运动的向心力是由弹簧弹力提供的,所以向心力也相等,由
又由
r甲+r乙=0.9 m
联立得r甲=0.3 m,r乙=0.6 m;半径大小代回向心力公式可得ω=0.6 rad/s。
故选D。
2.一般的曲线运动可以分成很多小段,每小段都可以看成圆周运动的一部分,即把整条曲线用一系列不同半径的小圆弧来代替.如图(a)所示,曲线上的A点的曲率圆定义为:通过A点和曲线上紧邻A点两侧的两点作一圆,在极限情况下,这个圆就叫做A点的曲率圆,其半径ρ叫做A点的曲率半径.现将一物体沿与水平面成α角的方向已速度υ0抛出,如图(b)所示.则在其轨迹最高点P处的曲率半径是
A. B.
C. D.
【答案】C
【详解】
物体在其轨迹最高点P处只有水平速度,其水平速度大小为,在最高点,把物体的运动看成圆周运动的一部分,物体的重力作为向心力,由向心力的公式得,所以在其轨迹最高点P处的曲率半径是:,故C正确.
【变式训练】
1.下列说法正确的是( )
A.做曲线运动的物体的速度大小一定变化
B.做曲线运动的物体一定有合外力,一定有加速度
C.平抛运动是变加速曲线运动
D.匀速圆周运动的向心力、向心加速度不变
【答案】B
【解析】A.做曲线运动的物体的速度大小不一定变化,但方向时刻改变,所以A错误;
B.做曲线运动的物体一定有合外力,一定有加速度,所以B正确;
C.平抛运动只受重力作用,所以是匀变速曲线运动,则C错误;
D.匀速圆周运动的向心力、向心加速度大小不变,但是方向时刻改变,所以D错误;
故选B。
2.A、B两物体在水平面上做匀速圆周运动。在相同时间内,它们通过的路程之比是4︰3,运动方向改变的角度之比是3︰2,则两物体做匀速圆周运动的( )
A.半径之比为2︰1 B.角速度大小之比为3︰4
C.线速度大小之比为4︰3 D.向心加速度大小之比为1︰2
【答案】C
【解析】ABC.因A、B时间相等内通过的路程之比为4︰3,根据线速度
则线速度之比为4︰3;
因运动方向改变的角度等于圆周运动转过的角度,A、B转过的角度之比为3︰2,时间相等,根据角速度
则角速度大小之比为3︰2;
根据
得圆周运动的半径,线速度之比为4︰3,角速度之比为3︰2,则圆周运动的半径之比为8︰9,故AB错误,C正确;
D.根据
得,线速度之比为4︰3,角速度之比为3︰2,则向心加速度之比为2︰1,故D错误。
故选C。
3.如图所示,皮带传动装置右轮的半径为r,a是它边缘上的一点;左侧为一轮轴,大轮的半径为4r,小轮的半径为2r,b点在小轮上,到小轮中心的距离为r,c点和d点分别位于小轮和大轮的边缘上。若在传动过程中,皮带不打滑,则( )
A.a点与b点的线速度大小相等
B.b点与d点的角速度大小不等
C.a点与d点的向心加速度大小相等
D.a、b、c、d四点中,向心加速度最小的是c点
【答案】C
【解析】A.由题意可得,a、c线速度大小相等, b、c角速度相等,由于,由
可得:,A错误;
B.由于b、d两点共轴转动,因此,B错误;
C.由题意可得,a、c线速度大小相等,由
可得:;
d、c角速度相等,由
可得:;
故a点与d点的向心加速度大小相等,C正确;
D.a点与d点的向心加速度大小相等,b、c、d角速度相等,根据
可得:向心加速度最小的是b点,D错误;
故选C。
4.如图所示,长为L的轻杆,一端固定有一个质量为m的可视为质点的小球,另一端固定在水平转轴O上,杆随转轴O在竖直平面内匀速转动,角速度为ω,某时刻杆对球的作用力为F,方向恰好与杆垂直,此时杆与水平面的夹角为θ.则下列关系正确的是
A.tanθ=g/(ω2L) B.sinθ=ω2L/g C.θ=0 D.F=mg/cosθ
【答案】B
【解析】小球所受重力和杆子的作用力的合力提供向心力,根据牛顿第二定律有,解得,故选项B正确,A、C、D错误.
5.两个质量相同的小球a、b用长度不等的细线拴在天花板上的同一点并在空中同一水平面内做匀速圆周运动,如图所示,则关于a、b两小球说法正确的是( )
A.a球角速度大于b球角速度
B.a球线速度大于b球线速度
C.a球向心力等于b球向心力
D.a球向心加速度小于b球向心加速度
【答案】B
【解析】A、对其中一个小球受力分析,如图,受重力,绳子的拉力,由于小球做匀速圆周运动,故合力提供向心力;
将重力与拉力合成,合力指向圆心,由几何关系得,合力:F=mgtanθ ①;
由向心力公式得到,F=mω2r ②;
设球与悬挂点间的高度差为h,由几何关系,得:r=htanθ ③;
由①②③三式得:,与绳子的长度和转动半径无关,与高度h有关;而两球圆周运动到悬点的高度相同,则有;故A错误;
B、因两球角速度相等,由v=wr,两球转动半径,则线速度,故B正确;
C、由F=mω2r,两球转动半径,而质量m和角速度相等,则向心力,故C错误;
D、由a=ω2r,角速度相等而转动半径,则向心加速度,故D错误;
故选B.
6.如图所示,为一皮带传动装置,右轮半径为r,a为它边缘上一点;左侧是一轮轴,大轮半径为4r,小轮半径为2r,b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若传动过程中皮带不打滑,则:( )
①a点和b点的线速度大小相等
②a点和b点的角速度大小相等
③a点和c点的线速度大小相等
④a点和d点的向心加速度大小相等
A.①③ B.②③ C.③④ D.②④
【答案】C
【解析】
a、c为共线关系,线速度相等,b、c为共轴关系,加速度相等,b、c的线速度不相等,①错;由v=wr可知,a、c的线速度相等,角速度不相等,②错;③对;设a的线速度为v,加速度为,c的线速度为v,角速度为,c、d角速度相同,d的线速度为2v,d的加速度为,④对;
7.如图所示,水平杆固定在竖直杆上,两者互相垂直,水平杆上O、A两点连接有两轻绳,两绳的另一端都系在质量为m的小球上,OA=OB=AB,现通过转动竖直杆,使水平杆在水平面内做匀速圆周运动,三角形OAB始终在竖直平面内,若转动过程中OB、AB两绳始终处于拉直状态,则下列说法正确的是( )
A.OB绳的拉力范围为0~mg
B.OB绳的拉力范围为mg~mg
C.AB绳的拉力范围为mg~mg
D.AB绳的拉力范围为0~mg
【答案】B
【解析】转动的角速度为零时,OB绳的拉力最小,AB绳的拉力最大,这时二者的值相同,设为T1,则有2T1cos30°=mg
解得T1=mg
增大转动的角速度,当AB绳的拉力刚好为零时,OB绳的拉力最大,设这时OB绳的拉力为T2,则有T2cos30°=mg
解得T2=mg
因此OB绳的拉力范围mg~mg,AB绳的拉力范围0~mg,故B正确,ACD错误。
故选B。
8.在探究向心力的大小与质量、角速度和半径之间关系的实验中,如图所示,是研究哪两个物理量之间的关系( )
A.研究向心力与质量之间的关系
B.研究向心力与角速度之间的关系
C.研究向心力与半径之间的关系
D.研究向心力与线速度之间的关系
【答案】A
【解析】铝球与钢球质量不同,转速相同,本实验研究向心力与质量之间的关系,不是研究向心力与角速度、半径、线速度的关系。
故选A。
