2020-2021学年高二上学期物理人教版选修3-1课件:3.6.1带电粒子在匀强磁场中的运动27 张PPT
文档属性
| 名称 | 2020-2021学年高二上学期物理人教版选修3-1课件:3.6.1带电粒子在匀强磁场中的运动27 张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 19.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-22 08:08:50 | ||
图片预览







文档简介
带电粒子
在匀强磁场中
的运动
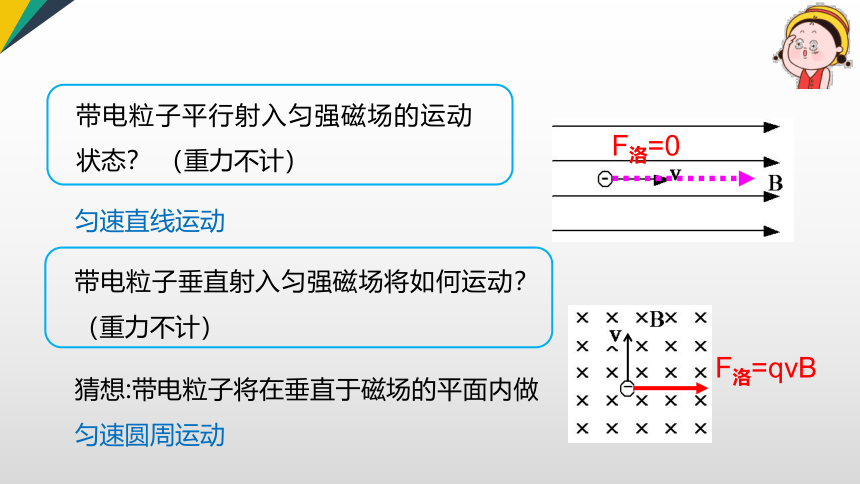
带电粒子平行射入匀强磁场的运动状态? (重力不计)
匀速直线运动
带电粒子垂直射入匀强磁场将如何运动? (重力不计)
猜想:带电粒子将在垂直于磁场的平面内做匀速圆周运动
F洛=qvB
F洛=0
v
-
F洛
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
v
-
F洛
v
-
F洛
v
-
F洛
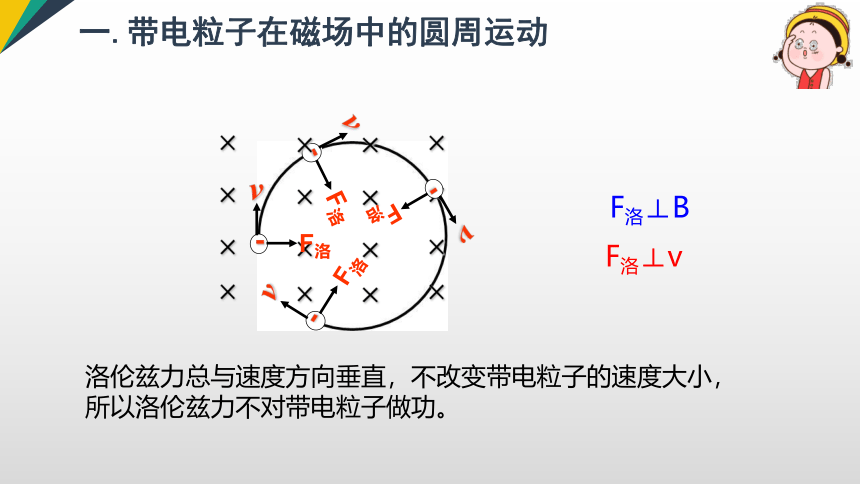
F洛⊥B
F洛⊥v
洛伦兹力总与速度方向垂直,不改变带电粒子的速度大小,所以洛伦兹力不对带电粒子做功。
一.带电粒子在磁场中的圆周运动
亥姆霍兹线圈
电 子 枪
磁场强弱选择挡
加速电压
选择挡
洛伦兹力演示器
带电粒子在磁场中的圆周运动
带电粒子在磁场中的圆周运动
不加磁场
加磁场
带电粒子在磁场中的圆周运动
带电粒子在匀强磁场中做匀速圆周运动
圆心一定在与速度方向垂直的直线上
带电粒子在磁场中的圆周运动
改变磁场
B大
B小
带电粒子在磁场中的圆周运动
粒子做圆周运动的半径与磁场强弱有关,半径随磁场的增强而减小
改变出射速度
v小
v大
带电粒子在磁场中的圆周运动
粒子做圆周运动的半径与粒子速度有关,半径随速度的增大而增大
1. 粒子做圆周运动的半径特征:
带电粒子在磁场中的圆周运动
r与速度v、磁感应强度B、粒子的比荷有关
适用条件:
(1)匀强磁场
(2)粒子垂直于磁场射入
v小
v大
2. 粒子做圆周运动的周期
带电粒子在磁场中的圆周运动
周期T与运动速度及运动半径无关
带电粒子在磁场中的圆周运动
周期仅与磁感应强度B,比荷 有关
带电粒子在气泡室运动径迹
由于能量损失,粒子的速度越来越小,故轨迹半径越来越小
带电粒子在磁场中的圆周运动
【例】一个质量为m、电荷量为q的粒子,从容器下方的小孔S1飘入电势差为U的加速电场,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上求:
(1)求粒子进入磁场时的速率
二.带电粒子在匀强磁场中运动的应用实例
···①
由①得,
【例】一个质量为m、电荷量为q的粒子,从容器下方的小孔S1飘入电势差为U的加速电场,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上求:
(2)求粒子在磁场中运动的轨道半径
带电粒子在匀强磁场中运动的应用实例
···②
由②得,
假设质子( )和氘核( )经过同一电场加速和同一磁场偏转,最后打在底片上D,它们的位置有何关系?
假设氘核( )和α粒子( )经过同一电场加速和同一磁场偏转,最后打在底片上D,它们的位置有何关系?
带电粒子在匀强磁场中运动的应用实例
1. 质谱仪
通过测出粒子圆周运动的半径,计算粒子的比荷或质量及分析同位素的仪器
带电粒子在匀强磁场中运动的应用实例
直线加速器
带电粒子在匀强磁场中运动的应用实例
带电粒子在匀强磁场中运动的应用实例
2. 回旋加速器
(2)工作原理
带电粒子在匀强磁场中运动的应用实例
粒子被加速后,运动速率和运动半径都会增加,它的运动周期会增加吗?
带电粒子在匀强磁场中运动的应用实例
【例】回旋加速器核心部分是两个D形金属扁盒,两盒和高频交流电源两极相接,在盒内的狭缝中形成匀强电场,使粒子每次穿过狭缝时都得到加速,两盒放在磁感应强度为B的匀强磁场中,磁场方向垂直于盒底面,粒子源射出的粒子电荷量为q,质量为m,粒子最大回旋半径为R。
(1)所加交变电流频率;
(2)粒子离开加速器时的最大速度及最大动能。
带电粒子在匀强磁场中运动的应用实例
交变电压的周期TE = 粒子在磁场中运动的周期TB
+
-
+
-
~
带电粒子在匀强磁场中运动的应用实例
【例】题目已知粒子电荷量为q,质量为m,粒子最大回旋半径为R.
(1)所加交变电流频率
提示:交流电的周期等于粒子做圆周运动的周期
带电粒子在匀强磁场中运动的应用实例
···①
···②
···③
由①②③得,
【例】题目已知粒子电荷量为q,质量为m,粒子最大回旋半径为R.
(2)粒子离开加速器时的最大速度及最大动能
提示:粒子运动半径等于D形盒时,速度最大,动能最大
带电粒子在匀强磁场中运动的应用实例
···④
···⑤
由④⑤得,
粒子的最终动能由磁感应强度B和D形盒的半径R决定
例1.一个带电粒子沿垂直于磁场方向射入一匀强磁场,粒子的一段运动径迹如图所示,径迹上每一小段可近似看成圆弧,由于带电粒子的运动使沿途的空气电离,粒子的动能逐渐减小(电量不变),从图中情况可以确定( )
A、粒子从a到b,带正电
B、粒子从b到a,带正电
C、粒子从a到b,带负电
D、粒子从b到a,带负电
B
典例分析
× × ×
× × ×
× × ×
× × ×
a。
b。
粒子动能减小,粒子的速度减小,故轨迹半径越来越小
利用左手定则判断电性
三、回旋加速器
?
由动能定理得带电粒子经几级的电场加速后增加的动能为Ek=q( U1+U2+U3+··········+Un )
新课教学
若需要很大的动能的粒子,利用直线加速器是否方便?为什么?那应该怎么办?
在匀强磁场中
的运动
带电粒子平行射入匀强磁场的运动状态? (重力不计)
匀速直线运动
带电粒子垂直射入匀强磁场将如何运动? (重力不计)
猜想:带电粒子将在垂直于磁场的平面内做匀速圆周运动
F洛=qvB
F洛=0
v
-
F洛
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
v
-
F洛
v
-
F洛
v
-
F洛
F洛⊥B
F洛⊥v
洛伦兹力总与速度方向垂直,不改变带电粒子的速度大小,所以洛伦兹力不对带电粒子做功。
一.带电粒子在磁场中的圆周运动
亥姆霍兹线圈
电 子 枪
磁场强弱选择挡
加速电压
选择挡
洛伦兹力演示器
带电粒子在磁场中的圆周运动
带电粒子在磁场中的圆周运动
不加磁场
加磁场
带电粒子在磁场中的圆周运动
带电粒子在匀强磁场中做匀速圆周运动
圆心一定在与速度方向垂直的直线上
带电粒子在磁场中的圆周运动
改变磁场
B大
B小
带电粒子在磁场中的圆周运动
粒子做圆周运动的半径与磁场强弱有关,半径随磁场的增强而减小
改变出射速度
v小
v大
带电粒子在磁场中的圆周运动
粒子做圆周运动的半径与粒子速度有关,半径随速度的增大而增大
1. 粒子做圆周运动的半径特征:
带电粒子在磁场中的圆周运动
r与速度v、磁感应强度B、粒子的比荷有关
适用条件:
(1)匀强磁场
(2)粒子垂直于磁场射入
v小
v大
2. 粒子做圆周运动的周期
带电粒子在磁场中的圆周运动
周期T与运动速度及运动半径无关
带电粒子在磁场中的圆周运动
周期仅与磁感应强度B,比荷 有关
带电粒子在气泡室运动径迹
由于能量损失,粒子的速度越来越小,故轨迹半径越来越小
带电粒子在磁场中的圆周运动
【例】一个质量为m、电荷量为q的粒子,从容器下方的小孔S1飘入电势差为U的加速电场,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上求:
(1)求粒子进入磁场时的速率
二.带电粒子在匀强磁场中运动的应用实例
···①
由①得,
【例】一个质量为m、电荷量为q的粒子,从容器下方的小孔S1飘入电势差为U的加速电场,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上求:
(2)求粒子在磁场中运动的轨道半径
带电粒子在匀强磁场中运动的应用实例
···②
由②得,
假设质子( )和氘核( )经过同一电场加速和同一磁场偏转,最后打在底片上D,它们的位置有何关系?
假设氘核( )和α粒子( )经过同一电场加速和同一磁场偏转,最后打在底片上D,它们的位置有何关系?
带电粒子在匀强磁场中运动的应用实例
1. 质谱仪
通过测出粒子圆周运动的半径,计算粒子的比荷或质量及分析同位素的仪器
带电粒子在匀强磁场中运动的应用实例
直线加速器
带电粒子在匀强磁场中运动的应用实例
带电粒子在匀强磁场中运动的应用实例
2. 回旋加速器
(2)工作原理
带电粒子在匀强磁场中运动的应用实例
粒子被加速后,运动速率和运动半径都会增加,它的运动周期会增加吗?
带电粒子在匀强磁场中运动的应用实例
【例】回旋加速器核心部分是两个D形金属扁盒,两盒和高频交流电源两极相接,在盒内的狭缝中形成匀强电场,使粒子每次穿过狭缝时都得到加速,两盒放在磁感应强度为B的匀强磁场中,磁场方向垂直于盒底面,粒子源射出的粒子电荷量为q,质量为m,粒子最大回旋半径为R。
(1)所加交变电流频率;
(2)粒子离开加速器时的最大速度及最大动能。
带电粒子在匀强磁场中运动的应用实例
交变电压的周期TE = 粒子在磁场中运动的周期TB
+
-
+
-
~
带电粒子在匀强磁场中运动的应用实例
【例】题目已知粒子电荷量为q,质量为m,粒子最大回旋半径为R.
(1)所加交变电流频率
提示:交流电的周期等于粒子做圆周运动的周期
带电粒子在匀强磁场中运动的应用实例
···①
···②
···③
由①②③得,
【例】题目已知粒子电荷量为q,质量为m,粒子最大回旋半径为R.
(2)粒子离开加速器时的最大速度及最大动能
提示:粒子运动半径等于D形盒时,速度最大,动能最大
带电粒子在匀强磁场中运动的应用实例
···④
···⑤
由④⑤得,
粒子的最终动能由磁感应强度B和D形盒的半径R决定
例1.一个带电粒子沿垂直于磁场方向射入一匀强磁场,粒子的一段运动径迹如图所示,径迹上每一小段可近似看成圆弧,由于带电粒子的运动使沿途的空气电离,粒子的动能逐渐减小(电量不变),从图中情况可以确定( )
A、粒子从a到b,带正电
B、粒子从b到a,带正电
C、粒子从a到b,带负电
D、粒子从b到a,带负电
B
典例分析
× × ×
× × ×
× × ×
× × ×
a。
b。
粒子动能减小,粒子的速度减小,故轨迹半径越来越小
利用左手定则判断电性
三、回旋加速器
?
由动能定理得带电粒子经几级的电场加速后增加的动能为Ek=q( U1+U2+U3+··········+Un )
新课教学
若需要很大的动能的粒子,利用直线加速器是否方便?为什么?那应该怎么办?
