六年级数学下册课件7.2.5立体图形的认识 苏教版 21张ppt
文档属性
| 名称 | 六年级数学下册课件7.2.5立体图形的认识 苏教版 21张ppt |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-22 12:16:41 | ||
图片预览




文档简介
(共21张PPT)
立体图形
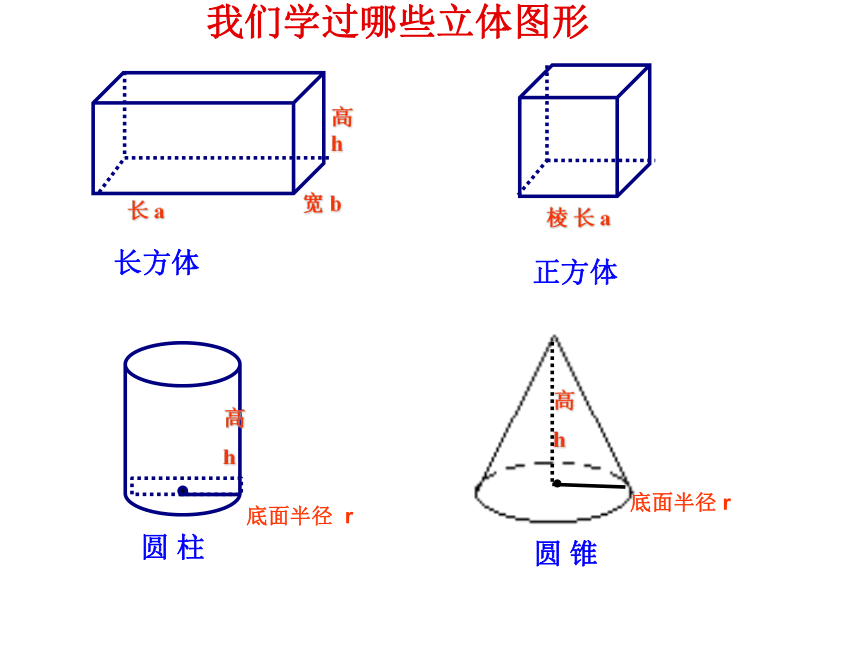
长
a
宽
b
高h
棱
长
a
长方体
正方体
圆
锥
圆
柱
高
h
高
h
底面半径
r
底面半径
r
我们学过哪些立体图形
小组讨论:
1、我们学过的立体图形各有什么特点?
2、长方体和正方体有什么相同点和不同点?
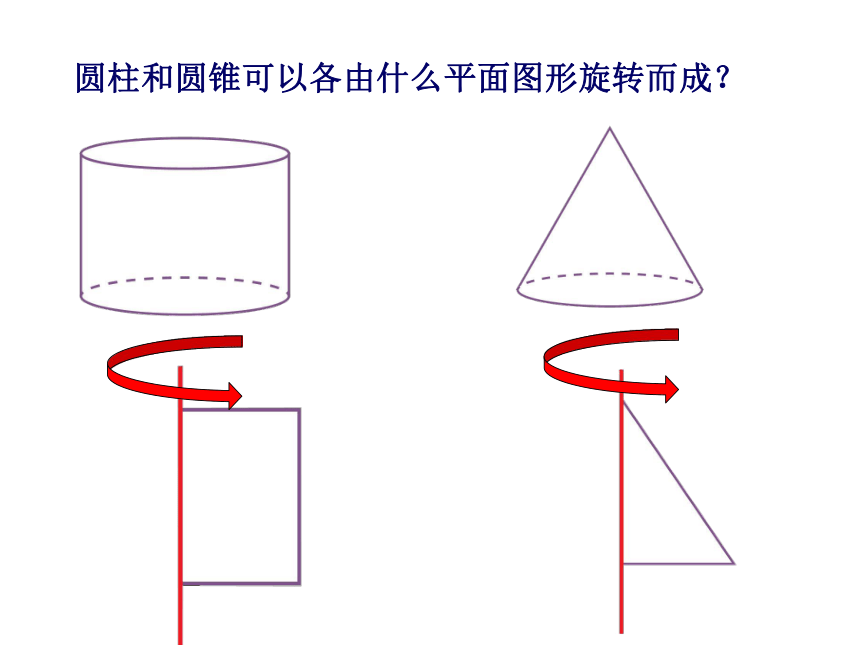
3、圆柱和圆锥可以各由什么平面图形旋转而成?
4、如何计算这些立体图形的表面积?
5、如何计算这些立体图形的体积?
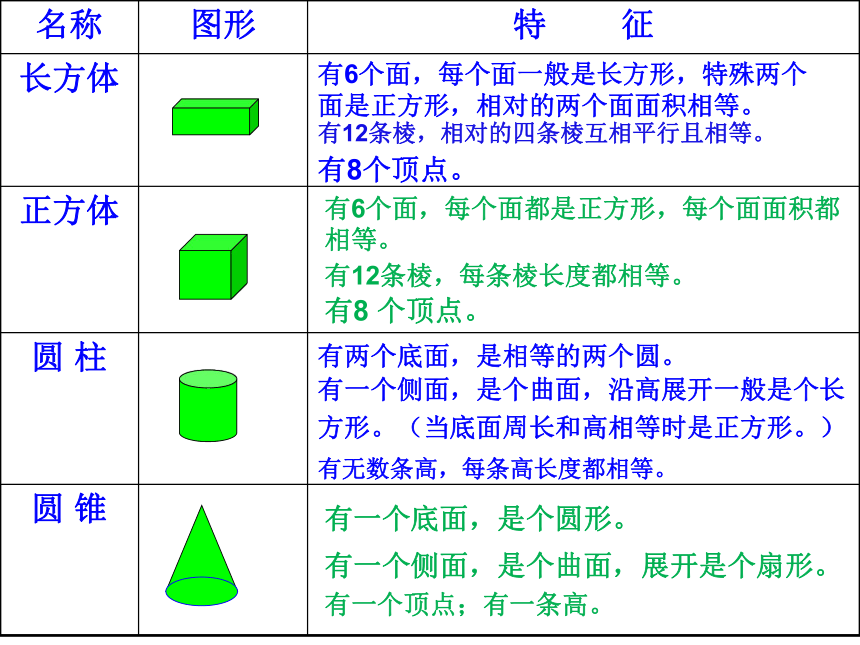
名称
图形
特
征
长方体
正方体
圆
柱
圆
锥
有12条棱,相对的四条棱互相平行且相等。
有12条棱,每条棱长度都相等。
有无数条高,每条高长度都相等。
有一个顶点;有一条高。
有6个面,每个面一般是长方形,特殊两个面是正方形,相对的两个面面积相等。
有8个顶点。
有6个面,每个面都是正方形,每个面面积都相等。
有8
个顶点。
有两个底面,是相等的两个圆。
有一个侧面,是个曲面,沿高展开一般是个长
方形。(当底面周长和高相等时是正方形。)
有一个底面,是个圆形。
有一个侧面,是个曲面,展开是个扇形。
圆柱和圆锥可以各由什么平面图形旋转而成?
练习一
①
圆柱的侧面展开一定是长方形。
(
)
②
这面小旗旋转一周产生的图形是圆锥体。(
)
③
一根长24厘米的铁丝制作成一个正方体框架,
棱长是3厘米。
(
)
√
×
×
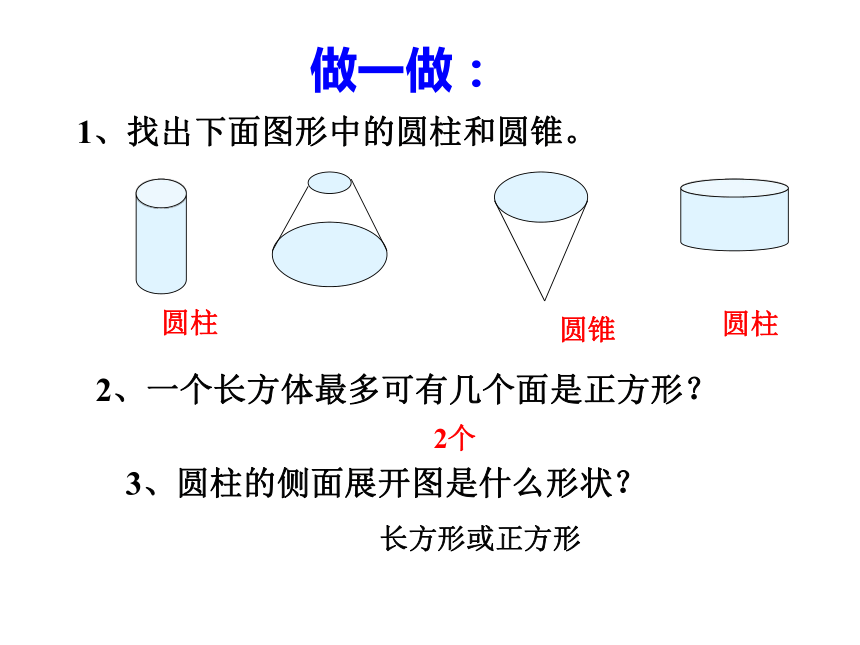
做一做:
2、一个长方体最多可有几个面是正方形?
1、找出下面图形中的圆柱和圆锥。
3、圆柱的侧面展开图是什么形状?
圆柱
圆锥
圆柱
2个
长方形或正方形
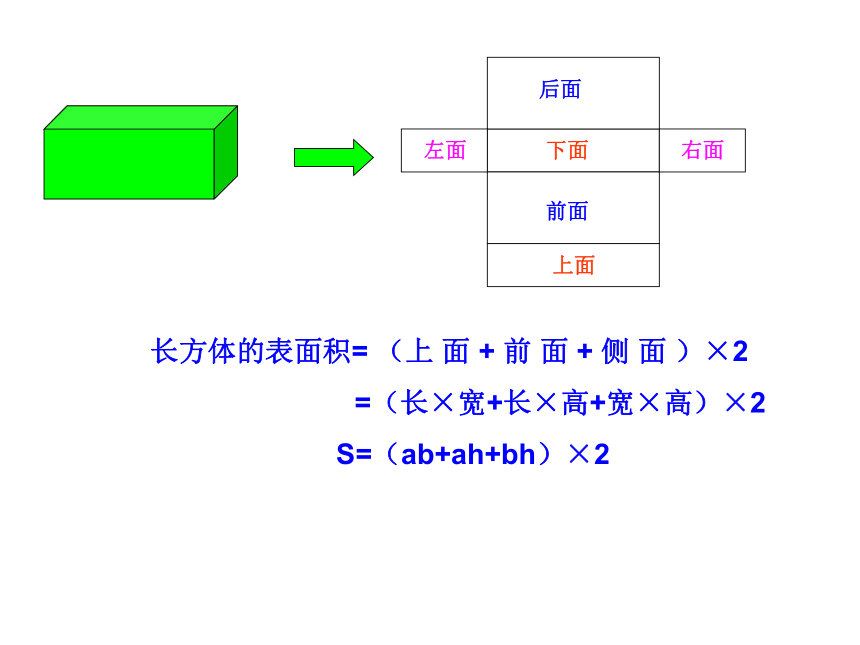
长方体的表面积=
(上
面
+
前
面
+
侧
面
)×2
=(长×宽+长×高+宽×高)×2
S=(ab+ah+bh)×2
下面
前面
后面
左面
右面
上面
正方体的表面积=一个面的面积×6
S=a2
×
6
圆柱的表面积=侧面积+底面积×2
S=ch+2
л
r2
=
2лrh+
2лr2
底面周长
高
底面
底面
侧面
长方体
正方体
圆柱
圆锥
物体所占空间的大小,
叫做物体的体积。
(1)每相邻的两个体积单位之间的进率是
1000。(
)
(2)圆锥的体积是圆柱的
。(
)
(3)
一个正方体的棱长是6分米,它的表面积与体积一样大。(
)
(4)两个圆柱的体积相等,它们的形状完全相同。(
)
(5)等底等高的长方体与圆柱体的体积相等。(
)
×
×
×
√
√
练习二
做一个圆柱形的无盖油箱,底面半径10分米,高0.5米。至少需要铁皮多少平方分米?
3.14
×102
+
2×3.14×10×5
=3.14
×100
+
2×3.14×10×5
=314+314
=628(平方分米)
用铁丝做一个长10厘米,宽5厘米,高4厘米的长方体框架,至少需要多长的铁丝?在这个长方体框架外面糊一层纸,至少需要多少平方厘米的纸?
10
5
4
(
10
+
5
+
4)×4=76
(厘米)
(10×5+10×4+5×4)×2=220(平方厘米)
(1)求至少需要多长的铁丝?
(2)求至少需要多少立方厘米的纸?
把一个底面半径是3分米,高是5分米的圆柱削成一个最大的圆锥,这个圆锥的体积是多少?
3.14
×32
×5
×
=47.1(立方分米)
(3)一个长方体水池,长15米,宽8米,池中水深1.57米,池底有根出水管,内直径0.2米,放水时,水流速度平均每秒流2米.放完池中的水需要多少分钟?
①池中水的体积.
生活中的数学
②水管每秒放水多少立方米?
③放完需要多少分钟?
(3)一个长方体水池,长15米,宽8米,池中水深1.57米,池底有根出水管,内直径0.2米,放水时,水流速度平均每秒流2米.放完池中的水需要多少分钟?
①池中水的体积.
生活中的数学
15×8×1.57=188.4(立方米)
(3)一个长方体水池,长15米,宽8米,池中水深1.57米,池底有根出水管,内直径0.2米,放水时,水流速度平均每秒流2米.放完池中的水需要多少分钟?
②水管每秒放水多少立方米?
生活中的数学
3.14×(0.2
÷
2)2×2=0.0628(立方米)
(3)一个长方体水池,长15米,宽8米,池中水深1.57米,池底有根出水管,内直径0.2米,放水时,水流速度平均每秒流2米.放完池中的水需要多少分钟?
③放完需要多少分钟?
生活中的数学
188.4÷
0.0628=3000(秒)
3000(秒)=50(分)
和同学们分享你的收获吧!
作业:
完成课文91页第12、14题。
立体图形
长
a
宽
b
高h
棱
长
a
长方体
正方体
圆
锥
圆
柱
高
h
高
h
底面半径
r
底面半径
r
我们学过哪些立体图形
小组讨论:
1、我们学过的立体图形各有什么特点?
2、长方体和正方体有什么相同点和不同点?
3、圆柱和圆锥可以各由什么平面图形旋转而成?
4、如何计算这些立体图形的表面积?
5、如何计算这些立体图形的体积?
名称
图形
特
征
长方体
正方体
圆
柱
圆
锥
有12条棱,相对的四条棱互相平行且相等。
有12条棱,每条棱长度都相等。
有无数条高,每条高长度都相等。
有一个顶点;有一条高。
有6个面,每个面一般是长方形,特殊两个面是正方形,相对的两个面面积相等。
有8个顶点。
有6个面,每个面都是正方形,每个面面积都相等。
有8
个顶点。
有两个底面,是相等的两个圆。
有一个侧面,是个曲面,沿高展开一般是个长
方形。(当底面周长和高相等时是正方形。)
有一个底面,是个圆形。
有一个侧面,是个曲面,展开是个扇形。
圆柱和圆锥可以各由什么平面图形旋转而成?
练习一
①
圆柱的侧面展开一定是长方形。
(
)
②
这面小旗旋转一周产生的图形是圆锥体。(
)
③
一根长24厘米的铁丝制作成一个正方体框架,
棱长是3厘米。
(
)
√
×
×
做一做:
2、一个长方体最多可有几个面是正方形?
1、找出下面图形中的圆柱和圆锥。
3、圆柱的侧面展开图是什么形状?
圆柱
圆锥
圆柱
2个
长方形或正方形
长方体的表面积=
(上
面
+
前
面
+
侧
面
)×2
=(长×宽+长×高+宽×高)×2
S=(ab+ah+bh)×2
下面
前面
后面
左面
右面
上面
正方体的表面积=一个面的面积×6
S=a2
×
6
圆柱的表面积=侧面积+底面积×2
S=ch+2
л
r2
=
2лrh+
2лr2
底面周长
高
底面
底面
侧面
长方体
正方体
圆柱
圆锥
物体所占空间的大小,
叫做物体的体积。
(1)每相邻的两个体积单位之间的进率是
1000。(
)
(2)圆锥的体积是圆柱的
。(
)
(3)
一个正方体的棱长是6分米,它的表面积与体积一样大。(
)
(4)两个圆柱的体积相等,它们的形状完全相同。(
)
(5)等底等高的长方体与圆柱体的体积相等。(
)
×
×
×
√
√
练习二
做一个圆柱形的无盖油箱,底面半径10分米,高0.5米。至少需要铁皮多少平方分米?
3.14
×102
+
2×3.14×10×5
=3.14
×100
+
2×3.14×10×5
=314+314
=628(平方分米)
用铁丝做一个长10厘米,宽5厘米,高4厘米的长方体框架,至少需要多长的铁丝?在这个长方体框架外面糊一层纸,至少需要多少平方厘米的纸?
10
5
4
(
10
+
5
+
4)×4=76
(厘米)
(10×5+10×4+5×4)×2=220(平方厘米)
(1)求至少需要多长的铁丝?
(2)求至少需要多少立方厘米的纸?
把一个底面半径是3分米,高是5分米的圆柱削成一个最大的圆锥,这个圆锥的体积是多少?
3.14
×32
×5
×
=47.1(立方分米)
(3)一个长方体水池,长15米,宽8米,池中水深1.57米,池底有根出水管,内直径0.2米,放水时,水流速度平均每秒流2米.放完池中的水需要多少分钟?
①池中水的体积.
生活中的数学
②水管每秒放水多少立方米?
③放完需要多少分钟?
(3)一个长方体水池,长15米,宽8米,池中水深1.57米,池底有根出水管,内直径0.2米,放水时,水流速度平均每秒流2米.放完池中的水需要多少分钟?
①池中水的体积.
生活中的数学
15×8×1.57=188.4(立方米)
(3)一个长方体水池,长15米,宽8米,池中水深1.57米,池底有根出水管,内直径0.2米,放水时,水流速度平均每秒流2米.放完池中的水需要多少分钟?
②水管每秒放水多少立方米?
生活中的数学
3.14×(0.2
÷
2)2×2=0.0628(立方米)
(3)一个长方体水池,长15米,宽8米,池中水深1.57米,池底有根出水管,内直径0.2米,放水时,水流速度平均每秒流2米.放完池中的水需要多少分钟?
③放完需要多少分钟?
生活中的数学
188.4÷
0.0628=3000(秒)
3000(秒)=50(分)
和同学们分享你的收获吧!
作业:
完成课文91页第12、14题。
