鲁教版(五四制)八年级下册数学9.1成比例线段课件(共16张PPT)
文档属性
| 名称 | 鲁教版(五四制)八年级下册数学9.1成比例线段课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 300.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-23 08:39:11 | ||
图片预览





文档简介
成比例线段
学习目标
1.理解两条线段的比、成比例线段的定义,掌握比例的基本性质及其应用.
2.进一步发展从数学角度发现问题、提出问题、解决问题的能力.
【情景引入】
观察下列图形,每一组图形有什么特点?
可以用相应线段长度的比来描述它们的大小关系。
(1)请从图中找出形状相同的图形,这些形状相同的图形有什么不同?
(2)怎样来描述它们的大小关系呢?
两条线段的比: 如果选用同一个长度单位量得两条线段AB,CD的长度分别是m、n;那么这两条线段的比就是两条线段的长度比。
其中,AB、CD分别叫做这个线段比的 、 。
前项
后项
【新知探究一】
同一个长度单位
长度比
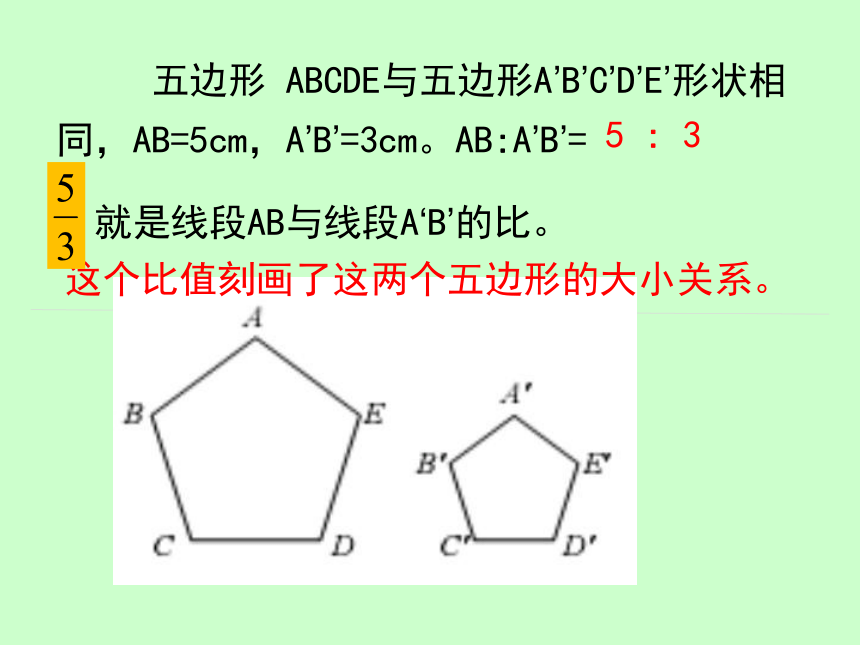
五边形 ABCDE与五边形A’B’C’D’E’形状相同,AB=5cm,A’B’=3cm。AB:A’B’=
就是线段AB与线段A‘B’的比。
这个比值刻画了这两个五边形的大小关系。
5 : 3
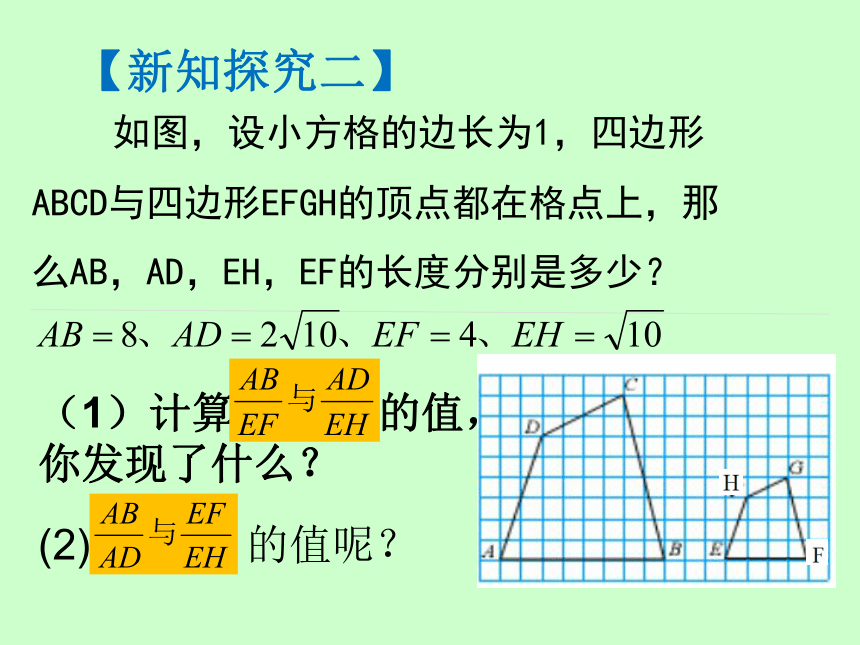
如图,设小方格的边长为1,四边形ABCD与四边形EFGH的顶点都在格点上,那么AB,AD,EH,EF的长度分别是多少?
【新知探究二】
(1)计算 的值, 你发现了什么?
(2) 的值呢?
四条线段a,b,c,d中,如果a与b的比等于c与d的比,即 ,那么这四条线段a,b,c,d叫做成比例线段,简称比例线段.
注意:比例线段是有顺序的!
成比例线段:
判断下列线段a,b,c,d是否是成比例线段:
a=4,b=6,c=5,d=10.
解:∵
∴ 线段a,b,c,d不是成比例线段.
,
∴
,
巩固练习
(1)如果a,b,c,d四个数成比例,即 那么ad=bc吗?
(2)反过来如果ad=bc,那么a,b,c,d四个数成比例吗?
【新知探究三】
分析:由等式的基本性质:
(1)在 两边同乘以bd,得ad=bc.
(2)若bd不等于0,由ad=bc两边同时除以bd得出 , 所以 a、b、c、d 四个数成比例。
对于问题(1),有没有其他方法,可以将分式形式为整式形式呢?
比例的基本性质
如果 ,那么
如果 那么
ad=bc
ad=bc
(a,b,c,d都不等于零)
变式训练
如果三个数a,b,c(a,b,c都不等于零)满足b?=ac,那么a,b,b,c是否成比例?
如图,一块矩形的长AB= m,宽AD=1m,按照图中所示的方式将它割成相同的三个矩形,且使割出的每个矩形的长与宽的比与原矩形的长与宽的比相同,即 那么 的值应当是多少?
【典例分析】
相同的三个矩形
巩固训练
如图,在△ABC中,AB=12cm,AE=6cm,EC=5cm,且
求AD的长.
【课堂小结】
知识上:掌握两条线段的比、成比例线段、比例基本性质及其应用
通过这节课,你有什么收获?与 交流一下......
思想方法上:转化的数学思想
学习目标
1.理解两条线段的比、成比例线段的定义,掌握比例的基本性质及其应用.
2.进一步发展从数学角度发现问题、提出问题、解决问题的能力.
【情景引入】
观察下列图形,每一组图形有什么特点?
可以用相应线段长度的比来描述它们的大小关系。
(1)请从图中找出形状相同的图形,这些形状相同的图形有什么不同?
(2)怎样来描述它们的大小关系呢?
两条线段的比: 如果选用同一个长度单位量得两条线段AB,CD的长度分别是m、n;那么这两条线段的比就是两条线段的长度比。
其中,AB、CD分别叫做这个线段比的 、 。
前项
后项
【新知探究一】
同一个长度单位
长度比
五边形 ABCDE与五边形A’B’C’D’E’形状相同,AB=5cm,A’B’=3cm。AB:A’B’=
就是线段AB与线段A‘B’的比。
这个比值刻画了这两个五边形的大小关系。
5 : 3
如图,设小方格的边长为1,四边形ABCD与四边形EFGH的顶点都在格点上,那么AB,AD,EH,EF的长度分别是多少?
【新知探究二】
(1)计算 的值, 你发现了什么?
(2) 的值呢?
四条线段a,b,c,d中,如果a与b的比等于c与d的比,即 ,那么这四条线段a,b,c,d叫做成比例线段,简称比例线段.
注意:比例线段是有顺序的!
成比例线段:
判断下列线段a,b,c,d是否是成比例线段:
a=4,b=6,c=5,d=10.
解:∵
∴ 线段a,b,c,d不是成比例线段.
,
∴
,
巩固练习
(1)如果a,b,c,d四个数成比例,即 那么ad=bc吗?
(2)反过来如果ad=bc,那么a,b,c,d四个数成比例吗?
【新知探究三】
分析:由等式的基本性质:
(1)在 两边同乘以bd,得ad=bc.
(2)若bd不等于0,由ad=bc两边同时除以bd得出 , 所以 a、b、c、d 四个数成比例。
对于问题(1),有没有其他方法,可以将分式形式为整式形式呢?
比例的基本性质
如果 ,那么
如果 那么
ad=bc
ad=bc
(a,b,c,d都不等于零)
变式训练
如果三个数a,b,c(a,b,c都不等于零)满足b?=ac,那么a,b,b,c是否成比例?
如图,一块矩形的长AB= m,宽AD=1m,按照图中所示的方式将它割成相同的三个矩形,且使割出的每个矩形的长与宽的比与原矩形的长与宽的比相同,即 那么 的值应当是多少?
【典例分析】
相同的三个矩形
巩固训练
如图,在△ABC中,AB=12cm,AE=6cm,EC=5cm,且
求AD的长.
【课堂小结】
知识上:掌握两条线段的比、成比例线段、比例基本性质及其应用
通过这节课,你有什么收获?与 交流一下......
思想方法上:转化的数学思想
