鲁教版(五四制)八年级下册数学9.2平行线分线段成比例课件(共20张PPT)
文档属性
| 名称 | 鲁教版(五四制)八年级下册数学9.2平行线分线段成比例课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 768.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-23 08:41:09 | ||
图片预览


文档简介
复习旧知 引入新课
1
1、什么是成比例线段?
2、若两条直线被一组平行线所截,
截得的线段是否成比例呢?
四条线段a,b,c,d中,如果
那么这四条线段a,b,c,d叫做成比例
线段,简称比例线段。
鲁教版五四制八年级下册第九章第二节
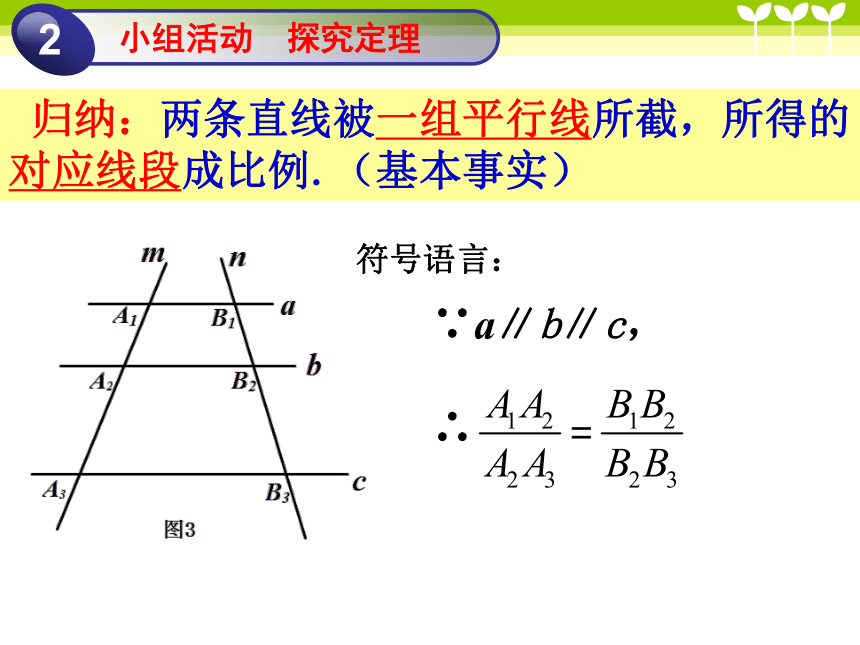
归纳:两条直线被一组平行线所截,所得的对应线段成比例.(基本事实)
∵a∥b∥c,
∴
符号语言:
小组活动 探究定理
2
议一议:
1.如何理解“对应线段”?
2.“对应线段”成比例都有哪些表达形式?
平行线
在直线m上截得的线段
在直线n上截得的线段
a‖b
b‖c
a‖c
A1A2 B1B2
A2A3 B2B3
A1A3 B1B3
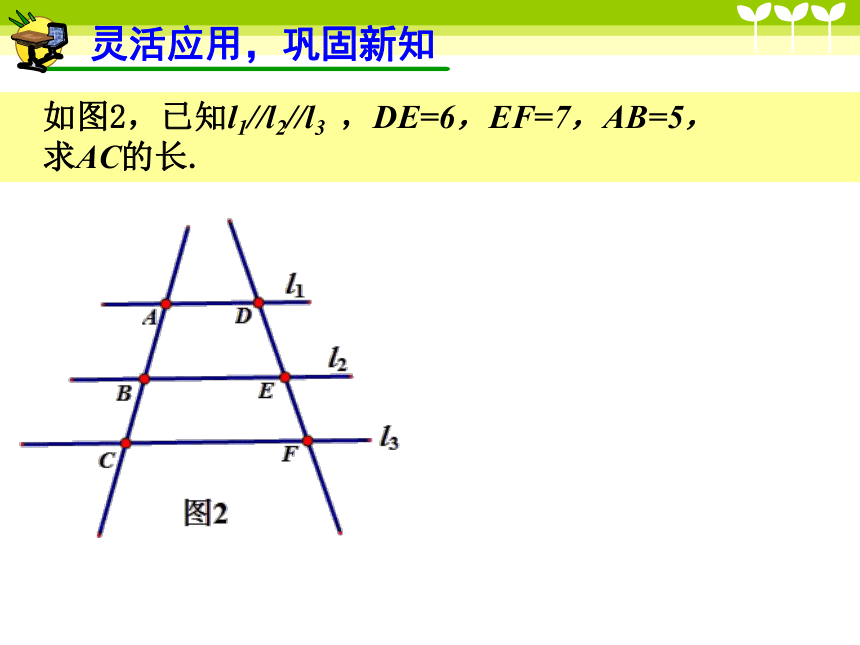
如图2,已知l1//l2//l3 ,DE=6,EF=7,AB=5,
求AC的长.
灵活应用,巩固新知
l1
l2
l3
A
B
C
D
E
F
m
n
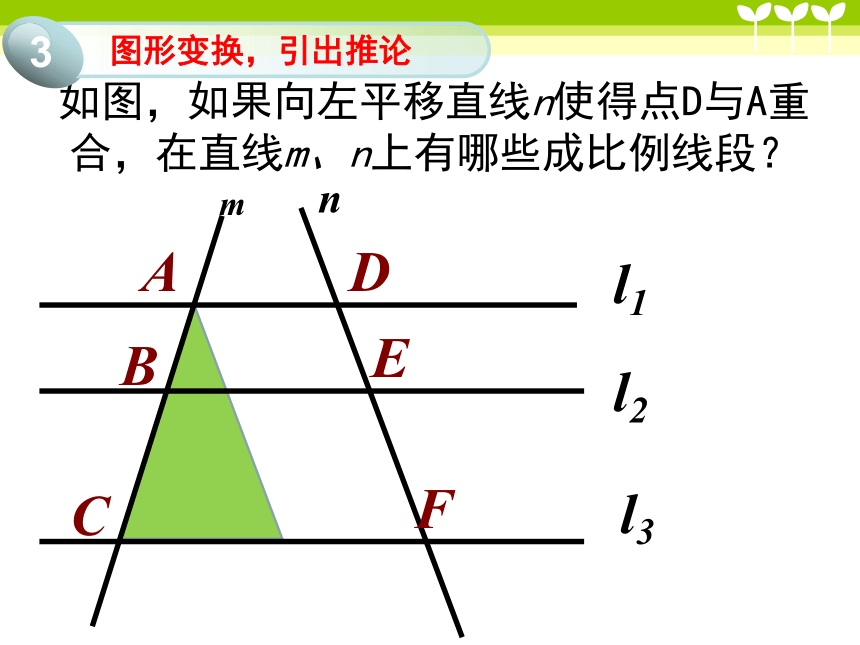
如图,如果向左平移直线n使得点D与A重合,在直线m、n上有哪些成比例线段?
图形变换,引出推论
3
A
B
C
E
F
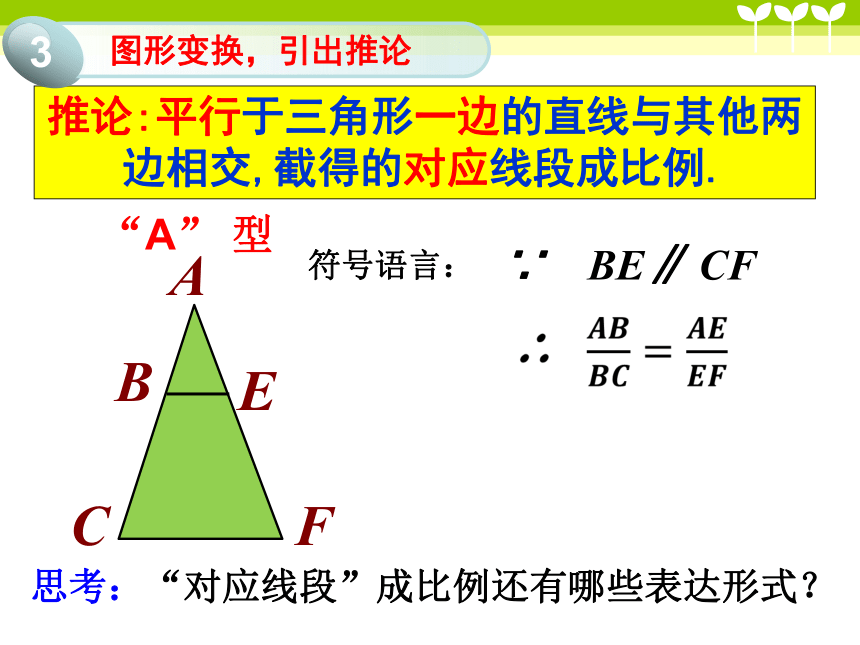
推论:平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.
“A” 型
图形变换,引出推论
3
∵ BE∥ CF
符号语言:
思考:“对应线段”成比例还有哪些表达形式?
l1
l2
l3
A
B
C
m
n
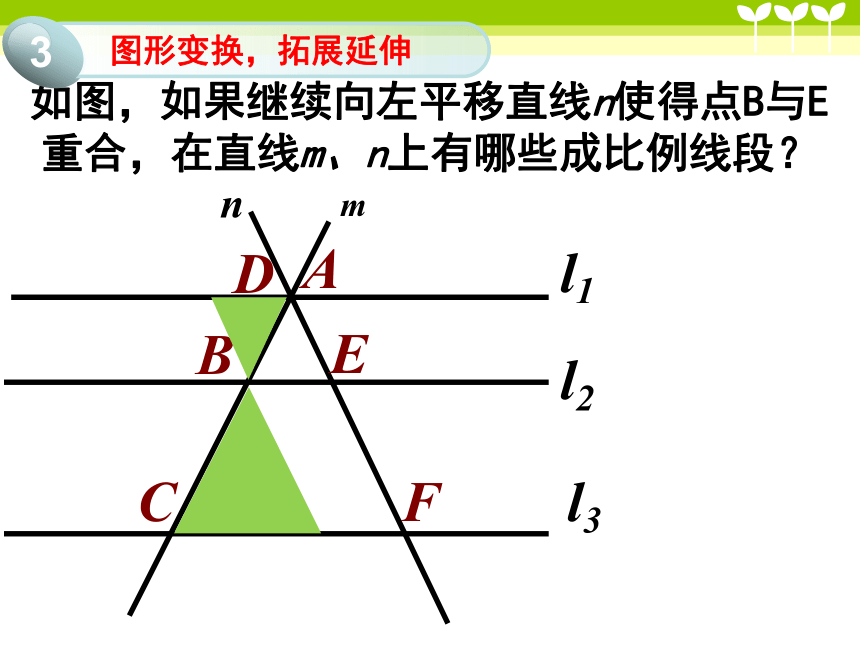
如图,如果继续向左平移直线n使得点B与E重合,在直线m、n上有哪些成比例线段?
E
F
D
图形变换,拓展延伸
3
A
B
C
F
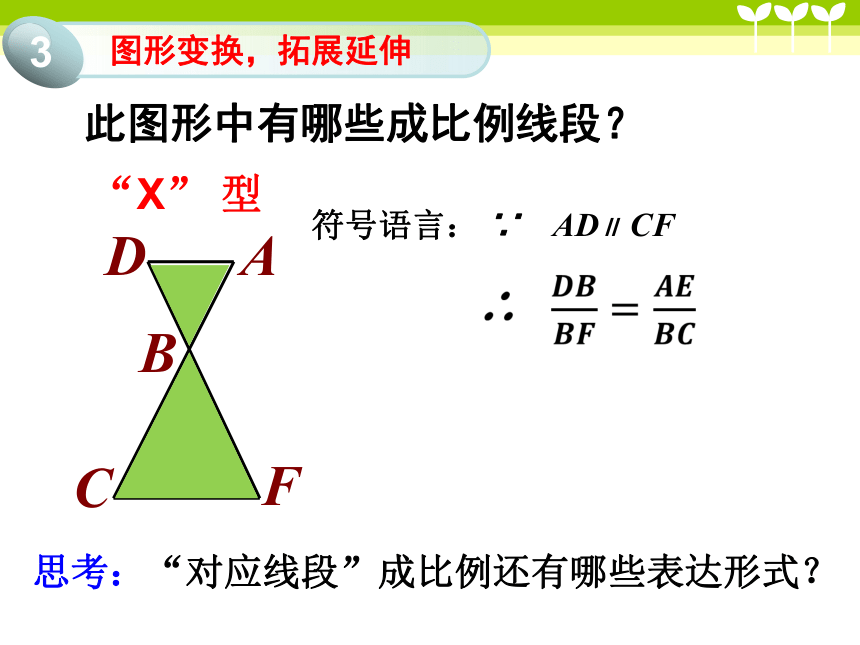
此图形中有哪些成比例线段?
D
“X” 型
∵ AD∥ CF
符号语言:
图形变换,拓展延伸
3
思考:“对应线段”成比例还有哪些表达形式?
A
B
E
C
D
1.(1)∵ AB∥DE
∴
CD
AD
=
( )
( )
AC
CD
=
( )
( )
BE
BC
=
( )
( )
A
B
C
F
D
G
E
(2)∵ AD∥EF ∥BC
=
( )
( )
∴
AG
GC
=
( )
( )
A
B
C
D
F
E
(3)已知平行四边形ABCD
则
AB
AE
=
( )
( )
CF
FB
=
( )
( )
CE
BE
BC
CE
AD
AC
AE
BE
DF
FC
DF
DE
DF
EF
灵活应用,巩固新知
2.如图3,已知l1//l2//l3 ,AB=5,BC=7,EF=4,
求DE的长
灵活应用,巩固新知
例:如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC。
(1)如果AE=7 ,EB=5,FC=4,求AF的长?
(2)如果AB=10, AE=6,AF=5,求EC的长?
A
B
C
F
E
典例解析
灵活应用 巩固新知
4
变式一:如图,在△ABC中,E,F分别是AB,AC上的点,且EF∥BC,AE:EB=2:3,若AF=6㎝,求AC 的长.
灵活应用 巩固新知
4
变式二:如图,在△ABC中,E,F分别是AB,AC上的点,且EF∥BC,AE:EB=2:3,
(1)求AF:FC的值.
(2)作DF∥AB,与BC 相交于点D,
若DC=30㎝,求BD 的值
反思小结 盘点收获
5
1.如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC。
(1)如果AD=6 ,DB=3,AE=4.
那么AC的长是多少?
(2)如果AB=5 ,AD=3,AC=4.
那么EC的长是多少?
A
B
C
E
D
课堂检测
2.如图,在△ABC中,D,E,F分别AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=2:3,
BC=20 cm,求BF的长
F
A
B
D
E
C
能力提升
B
C
A
D
E
能力提升
在数学天地里,重要的不是我们知道什么,而是我们怎么知道。
—— 毕达哥拉斯
结束寄语
1
1、什么是成比例线段?
2、若两条直线被一组平行线所截,
截得的线段是否成比例呢?
四条线段a,b,c,d中,如果
那么这四条线段a,b,c,d叫做成比例
线段,简称比例线段。
鲁教版五四制八年级下册第九章第二节
归纳:两条直线被一组平行线所截,所得的对应线段成比例.(基本事实)
∵a∥b∥c,
∴
符号语言:
小组活动 探究定理
2
议一议:
1.如何理解“对应线段”?
2.“对应线段”成比例都有哪些表达形式?
平行线
在直线m上截得的线段
在直线n上截得的线段
a‖b
b‖c
a‖c
A1A2 B1B2
A2A3 B2B3
A1A3 B1B3
如图2,已知l1//l2//l3 ,DE=6,EF=7,AB=5,
求AC的长.
灵活应用,巩固新知
l1
l2
l3
A
B
C
D
E
F
m
n
如图,如果向左平移直线n使得点D与A重合,在直线m、n上有哪些成比例线段?
图形变换,引出推论
3
A
B
C
E
F
推论:平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.
“A” 型
图形变换,引出推论
3
∵ BE∥ CF
符号语言:
思考:“对应线段”成比例还有哪些表达形式?
l1
l2
l3
A
B
C
m
n
如图,如果继续向左平移直线n使得点B与E重合,在直线m、n上有哪些成比例线段?
E
F
D
图形变换,拓展延伸
3
A
B
C
F
此图形中有哪些成比例线段?
D
“X” 型
∵ AD∥ CF
符号语言:
图形变换,拓展延伸
3
思考:“对应线段”成比例还有哪些表达形式?
A
B
E
C
D
1.(1)∵ AB∥DE
∴
CD
AD
=
( )
( )
AC
CD
=
( )
( )
BE
BC
=
( )
( )
A
B
C
F
D
G
E
(2)∵ AD∥EF ∥BC
=
( )
( )
∴
AG
GC
=
( )
( )
A
B
C
D
F
E
(3)已知平行四边形ABCD
则
AB
AE
=
( )
( )
CF
FB
=
( )
( )
CE
BE
BC
CE
AD
AC
AE
BE
DF
FC
DF
DE
DF
EF
灵活应用,巩固新知
2.如图3,已知l1//l2//l3 ,AB=5,BC=7,EF=4,
求DE的长
灵活应用,巩固新知
例:如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC。
(1)如果AE=7 ,EB=5,FC=4,求AF的长?
(2)如果AB=10, AE=6,AF=5,求EC的长?
A
B
C
F
E
典例解析
灵活应用 巩固新知
4
变式一:如图,在△ABC中,E,F分别是AB,AC上的点,且EF∥BC,AE:EB=2:3,若AF=6㎝,求AC 的长.
灵活应用 巩固新知
4
变式二:如图,在△ABC中,E,F分别是AB,AC上的点,且EF∥BC,AE:EB=2:3,
(1)求AF:FC的值.
(2)作DF∥AB,与BC 相交于点D,
若DC=30㎝,求BD 的值
反思小结 盘点收获
5
1.如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC。
(1)如果AD=6 ,DB=3,AE=4.
那么AC的长是多少?
(2)如果AB=5 ,AD=3,AC=4.
那么EC的长是多少?
A
B
C
E
D
课堂检测
2.如图,在△ABC中,D,E,F分别AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=2:3,
BC=20 cm,求BF的长
F
A
B
D
E
C
能力提升
B
C
A
D
E
能力提升
在数学天地里,重要的不是我们知道什么,而是我们怎么知道。
—— 毕达哥拉斯
结束寄语
