鲁教版(五四制)八年级下册数学9.6黄金分割课件(共17张PPT)
文档属性
| 名称 | 鲁教版(五四制)八年级下册数学9.6黄金分割课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-23 08:44:18 | ||
图片预览



文档简介
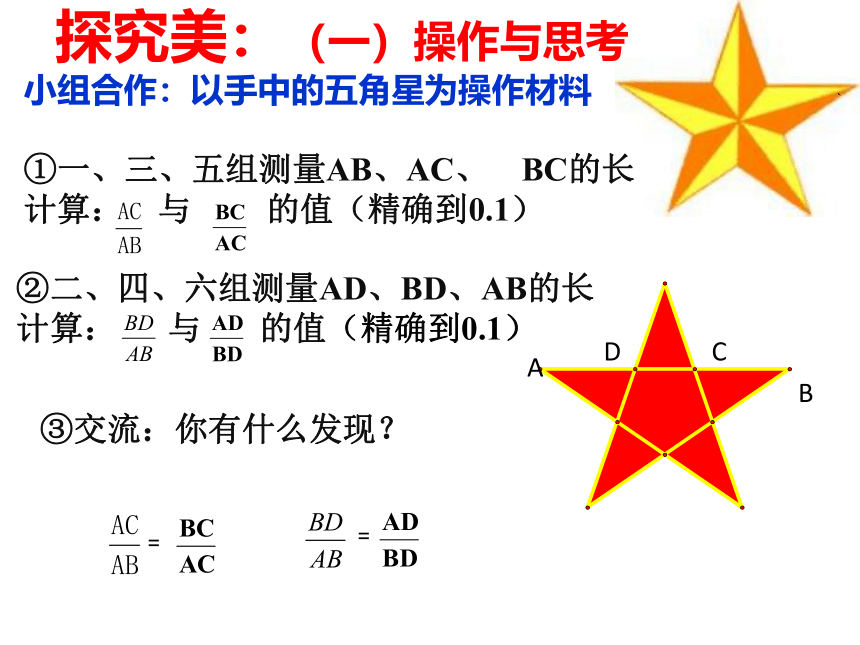
探究美:(一)操作与思考
小组合作:以手中的五角星为操作材料
①一、三、五组测量AB、AC、 BC的长
计算: 与 的值(精确到0.1)
、
②二、四、六组测量AD、BD、AB的长
计算: 与 的值(精确到0.1)
③交流:你有什么发现?
A
C
B
D
=
=
活动一:探究黄金分割的定义
(自学课本P110—111)
②你认为一条线段上有几个黄金分割点?
③什么叫黄金比?
①什么叫做黄金分割?黄金分割点?
(二)自学与思考
思考:
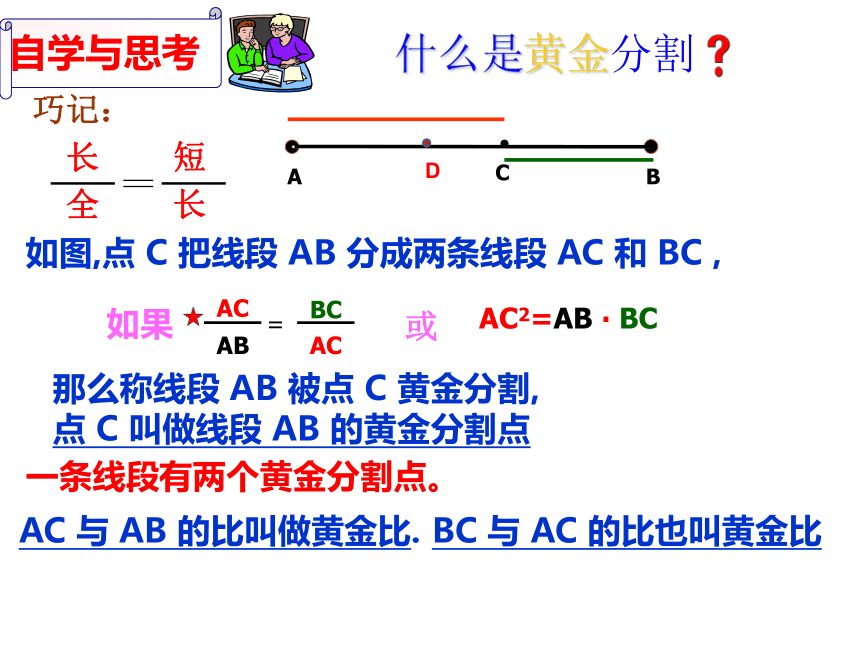
如图,点 C 把线段 AB 分成两条线段 AC 和 BC ,
如果
AC
AB
AC
BC
=
那么称线段 AB 被点 C 黄金分割,
点 C 叫做线段 AB 的黄金分割点
AC 与 AB 的比叫做黄金比.
C
A
B
AC2=AB ? BC
自学与思考
什么是黄金分割
长
全
短
长
巧记:
或
BC 与 AC 的比也叫黄金比
一条线段有两个黄金分割点。
D
活动二:求黄金比
(自学课本P110—111)
思考:
①如何求黄金比?求黄金比需要用到什么数学思想?
②如何判断某点是线段的黄金分割点?
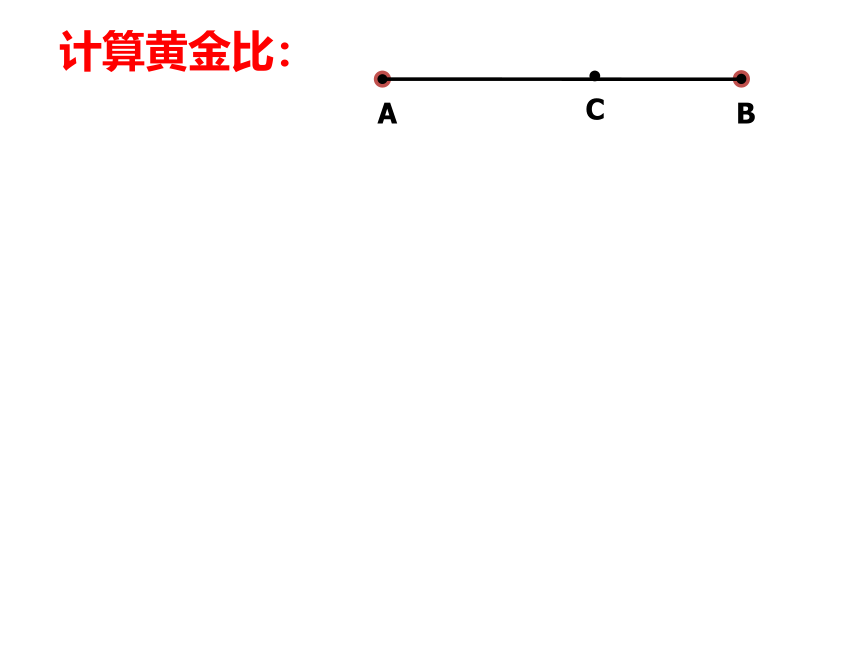
已知:点C是线段AB的黄金分割点,你能求出黄金比的准确值吗?
探究交流
计算黄金比:
C
A
B
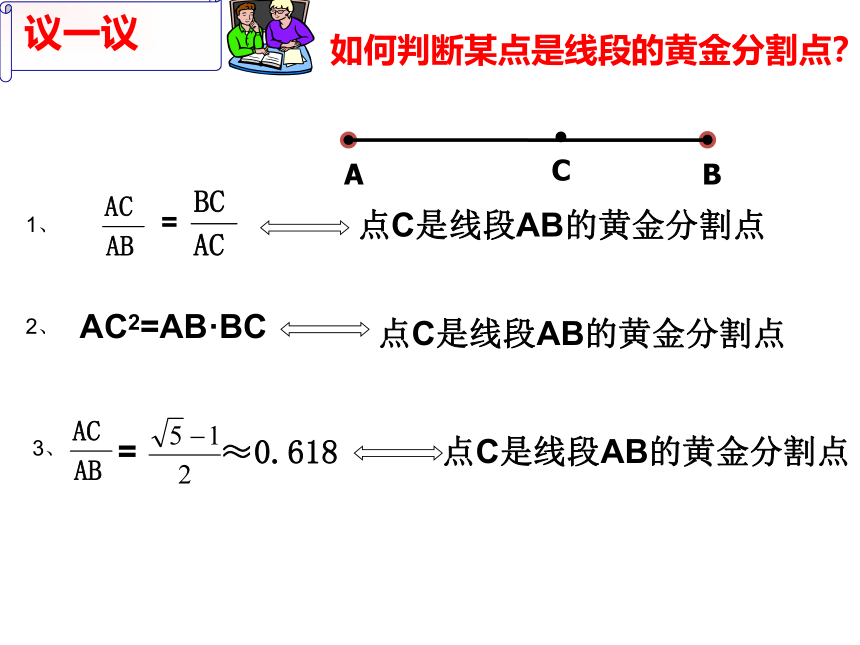
如何判断某点是线段的黄金分割点?
议一议
C
A
B
=
1、
点C是线段AB的黄金分割点
2、
AC2=AB·BC
点C是线段AB的黄金分割点
3、
=
点C是线段AB的黄金分割点
≈0.618
h
0.618h
衡量一个人的身材是否美观的标准:
肚脐是否头顶到脚底的黄金分割点。
即:肚脐到脚底的距离与身高的比近似0.618
黄金分割与人体美学
揭 示 美
古希腊时期的巴台农神庙
为什么如此震撼、壮观?
如图是古希腊时期的巴台农神庙, 如果把图中虚线表示的矩形画成下图中的矩形ABEF
A
B
E
F
这个矩形ABEF很美观,这其中存在的奥秘是什么?
揭 示 美
古希腊时期的
巴台农神庙
A
B
E
F
C
D
以矩形ABEF的宽为边在其内部作正方形ACDF,那么我们惊奇的发现:
你能得出什么结论?矩形的宽与长的比是多少?
1、点C是线段AB的黄金分割点
=
我们称宽与长的比是黄金比的矩形是黄金矩形。
2、
1.你能为老师设计一双使身材更美的高跟鞋吗?
应 用 美
已知:老师的身高164cm,肚脐到脚底的距离是99cm,
鞋跟多高身材最美?(取近似值)
2.
已知:在△ABC中,AB=AC,∠BAC=36°,
BD平分∠ABC,
求证:①AD=BD=BC ②△ABC∽△BDC
③小明说,图中的点D是线段AC的黄金分割点,小明说的对吗?为什么?
收 获 美
1、这节课我的收获是——
2、耐人寻味的0.618(音频故事)
课堂检测
1、
2、如图,在 中,点E为边BC的黄金分割点(BE>EC)AE 与BD相交于点F。
求: 的值
□ABCD
3、顶角为36?的等腰三角形称为黄金三角形(底与腰的比
为 的三角形)如图,在△ABC中,AB=AC ,
∠ABC=72°,BD、DE分别平分∠ABC ∠BDC ,那么图中的黄金三角形有____个,当AB=4时,DE=________.
能力提高:
上海东方明珠塔高463米,设计师为了美观,在靠近顶端
的黄金分割点处设计了一个球体,请问这个球距地面多高?
实践美
1、给妈妈设计一双使身材最美的高跟鞋
2、查阅有关黄金分割的资料
再 见
E
C
A
B
D
能力提高
用下面的方法作已知线段AB的黄金分割点。
①连B作BD⊥AB,使BD= AB
②连接AD,在DA上截取 DE=DB
③在AB上截取AC=AE,点C即AB的黄金分割点,
你能说出其中的道理吗?
设AB=2x, 则BD=x
∵∠ABD=90?
∴AD=
∵DE=BD=x
∴AE= -x =
∴AC=
∴
小组合作:以手中的五角星为操作材料
①一、三、五组测量AB、AC、 BC的长
计算: 与 的值(精确到0.1)
、
②二、四、六组测量AD、BD、AB的长
计算: 与 的值(精确到0.1)
③交流:你有什么发现?
A
C
B
D
=
=
活动一:探究黄金分割的定义
(自学课本P110—111)
②你认为一条线段上有几个黄金分割点?
③什么叫黄金比?
①什么叫做黄金分割?黄金分割点?
(二)自学与思考
思考:
如图,点 C 把线段 AB 分成两条线段 AC 和 BC ,
如果
AC
AB
AC
BC
=
那么称线段 AB 被点 C 黄金分割,
点 C 叫做线段 AB 的黄金分割点
AC 与 AB 的比叫做黄金比.
C
A
B
AC2=AB ? BC
自学与思考
什么是黄金分割
长
全
短
长
巧记:
或
BC 与 AC 的比也叫黄金比
一条线段有两个黄金分割点。
D
活动二:求黄金比
(自学课本P110—111)
思考:
①如何求黄金比?求黄金比需要用到什么数学思想?
②如何判断某点是线段的黄金分割点?
已知:点C是线段AB的黄金分割点,你能求出黄金比的准确值吗?
探究交流
计算黄金比:
C
A
B
如何判断某点是线段的黄金分割点?
议一议
C
A
B
=
1、
点C是线段AB的黄金分割点
2、
AC2=AB·BC
点C是线段AB的黄金分割点
3、
=
点C是线段AB的黄金分割点
≈0.618
h
0.618h
衡量一个人的身材是否美观的标准:
肚脐是否头顶到脚底的黄金分割点。
即:肚脐到脚底的距离与身高的比近似0.618
黄金分割与人体美学
揭 示 美
古希腊时期的巴台农神庙
为什么如此震撼、壮观?
如图是古希腊时期的巴台农神庙, 如果把图中虚线表示的矩形画成下图中的矩形ABEF
A
B
E
F
这个矩形ABEF很美观,这其中存在的奥秘是什么?
揭 示 美
古希腊时期的
巴台农神庙
A
B
E
F
C
D
以矩形ABEF的宽为边在其内部作正方形ACDF,那么我们惊奇的发现:
你能得出什么结论?矩形的宽与长的比是多少?
1、点C是线段AB的黄金分割点
=
我们称宽与长的比是黄金比的矩形是黄金矩形。
2、
1.你能为老师设计一双使身材更美的高跟鞋吗?
应 用 美
已知:老师的身高164cm,肚脐到脚底的距离是99cm,
鞋跟多高身材最美?(取近似值)
2.
已知:在△ABC中,AB=AC,∠BAC=36°,
BD平分∠ABC,
求证:①AD=BD=BC ②△ABC∽△BDC
③小明说,图中的点D是线段AC的黄金分割点,小明说的对吗?为什么?
收 获 美
1、这节课我的收获是——
2、耐人寻味的0.618(音频故事)
课堂检测
1、
2、如图,在 中,点E为边BC的黄金分割点(BE>EC)AE 与BD相交于点F。
求: 的值
□ABCD
3、顶角为36?的等腰三角形称为黄金三角形(底与腰的比
为 的三角形)如图,在△ABC中,AB=AC ,
∠ABC=72°,BD、DE分别平分∠ABC ∠BDC ,那么图中的黄金三角形有____个,当AB=4时,DE=________.
能力提高:
上海东方明珠塔高463米,设计师为了美观,在靠近顶端
的黄金分割点处设计了一个球体,请问这个球距地面多高?
实践美
1、给妈妈设计一双使身材最美的高跟鞋
2、查阅有关黄金分割的资料
再 见
E
C
A
B
D
能力提高
用下面的方法作已知线段AB的黄金分割点。
①连B作BD⊥AB,使BD= AB
②连接AD,在DA上截取 DE=DB
③在AB上截取AC=AE,点C即AB的黄金分割点,
你能说出其中的道理吗?
设AB=2x, 则BD=x
∵∠ABD=90?
∴AD=
∵DE=BD=x
∴AE= -x =
∴AC=
∴
