2020-2021学年苏科 版七年级数学下册12.2 证明(1)课件(19张ppt)
文档属性
| 名称 | 2020-2021学年苏科 版七年级数学下册12.2 证明(1)课件(19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-23 11:46:23 | ||
图片预览



文档简介
(共19张PPT)
初中数学七年级下册
(苏科版)
12.2
证明(1)
12.2 证明(1)
【创设情境】同学们听说过或见过海市蜃楼吗?
夏天,平静无风的海面或沙漠上,有时能看到楼台、亭阁、集市、庙宇等虚幻景象出现在远方的空中……
自然界中看到的景象是真实存在的吗?
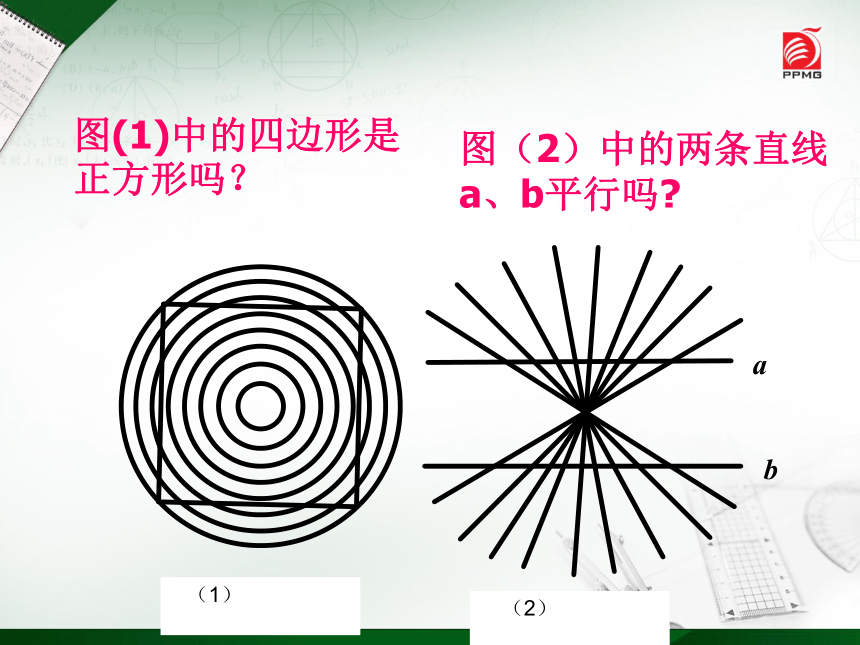
图(1)中的四边形是正方形吗?
(1)
(2)
图(2)中的两条直线a、b平行吗?
创设情境
12.2 证明⑴
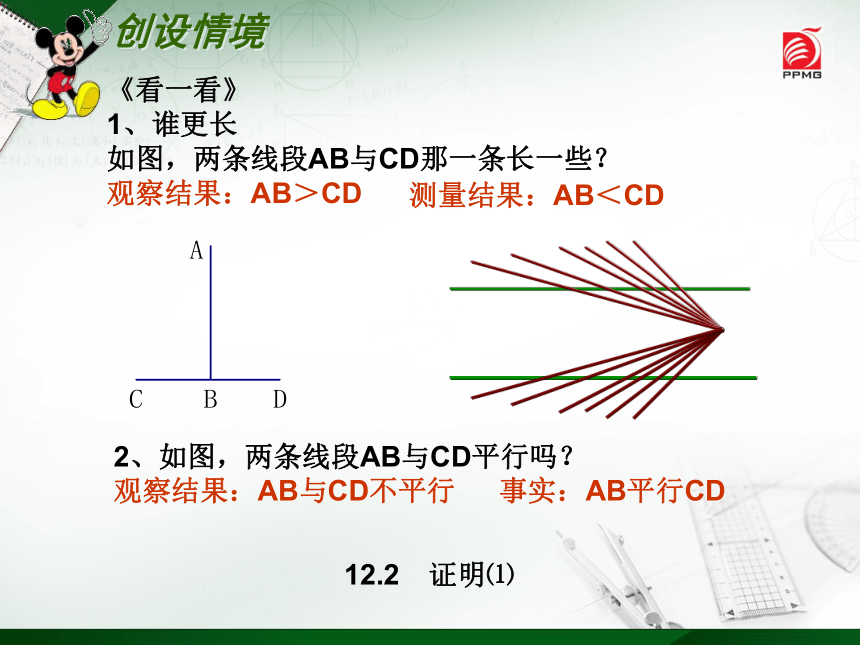
《看一看》
1、谁更长
如图,两条线段AB与CD那一条长一些?
观察结果:AB>CD
2、如图,两条线段AB与CD平行吗?
观察结果:AB与CD不平行
测量结果:AB<CD
事实:AB平行CD
新知探究
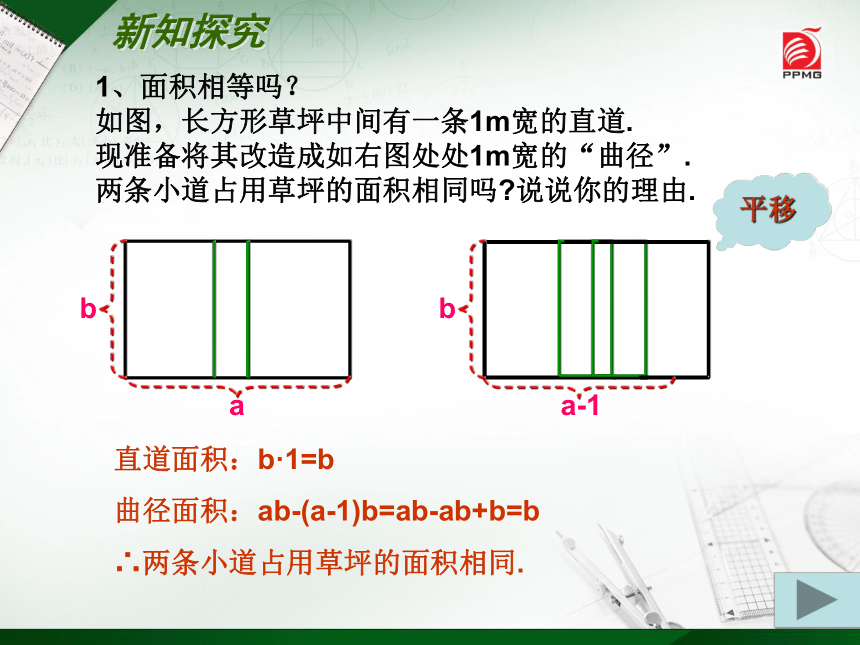
1、面积相等吗?
如图,长方形草坪中间有一条1m宽的直道.
现准备将其改造成如右图处处1m宽的“曲径”.
两条小道占用草坪的面积相同吗?说说你的理由.
a
b
直道面积:b·1=b
曲径面积:ab-(a-1)b=ab-ab+b=b
∴两条小道占用草坪的面积相同.
平移
a-1
b
新知探究
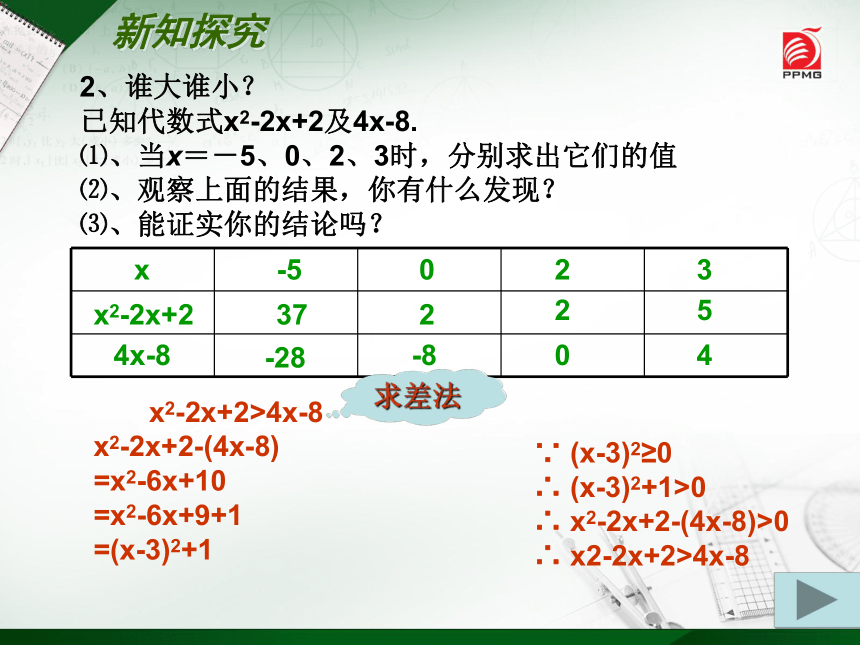
2、谁大谁小?
已知代数式x2-2x+2及4x-8.
⑴、当x=-5、0、2、3时,分别求出它们的值
⑵、观察上面的结果,你有什么发现?
⑶、能证实你的结论吗?
x
x2-2x+2
4x-8
-5
0
2
3
37
-28
2
-8
2
0
4
5
x2-2x+2>4x-8
x2-2x+2-(4x-8)
=x2-6x+10
=x2-6x+9+1
=(x-3)2+1
求差法
∵
(x-3)2≥0
∴
(x-3)2+1>0
∴
x2-2x+2-(4x-8)>0
∴
x2-2x+2>4x-8
新知探究
3、它们平行吗?
六边形ABCDEF的每一个内角都是相等的,∠1=60°,那么AB与ED,AD与EF有怎样的位置关系?
∵六边形每一个内角都是相等
∴∠F=∠FAB=∠B=∠C=∠CDE=
∵∠1=60°
∴∠2=120°-60°=
60°
∴∠2+∠F=180°
∴AD
∥EF
∵
四边形ABCD
∴∠1+∠B+∠C+∠3=360°
∴∠3=360°-120°-120°-60°=60°
∴∠4=120°-60°=60°
∴∠1=∠4
∴AB∥ED
2
3
4
新知探究
《议一议》在确定上面三个数学结论的正确性时, 我们运用了哪些数学知识?运用了哪些数学方法?
知 识:平移、长方形面积、整式的加减、完全平方公式、非负数、多边形内角和、两直线平行的条件等.
数学方法:平移法、求差法、配方法等.
《读一读》观察、实验、操作中得出的结论还需要运用已学过的数学知识和方法来证明它的正确性.
图(1)
图(1)中有曲线吗?
课堂练习
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
请把图(2)中编号相同的点用线段连接起来.
图(1)
图(2)
图(1)中有曲线吗?
课堂练习
课本149练一练第1、2、3题
下图正中央的两个圆全等吗?
课堂练习
课本149练一练第1、2、3题
数学实验室
《拼一拼》
如图①是一张8㎝×8㎝的正方形纸片.
有人说可将它剪成4块重新拼合,拼成像图②那样长为13,宽为5的长方形.
你认为这可能吗?
不能,因为图①的面积64,而图②的面积为65.
数学实验室
《量一量》
如图,画∠AOB,并画∠AOB的角平分线OC
⑴、将三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别交于点E、F,量一量PE、PF的长度,猜想它们之间有何关系?
⑵、把三角尺绕点P旋转,⑴中的结论还成立吗?
相等
还成立
回顾反思
本节课,我们有哪些收获?
1、仅凭观察、实验、操作得到的结论有时是表面的,片面的,是不够深入,是不够全面的,甚至有时是错误的
2、观察、实验、操作中得出的结论还需要运用已学过的数学知识和方法来证明它的正确性.
3、证明是必要的.
课本154页习题第1、2题
布置作业
课本154页习题第1、2题
谢
谢!
初中数学七年级下册
(苏科版)
12.2
证明(1)
12.2 证明(1)
【创设情境】同学们听说过或见过海市蜃楼吗?
夏天,平静无风的海面或沙漠上,有时能看到楼台、亭阁、集市、庙宇等虚幻景象出现在远方的空中……
自然界中看到的景象是真实存在的吗?
图(1)中的四边形是正方形吗?
(1)
(2)
图(2)中的两条直线a、b平行吗?
创设情境
12.2 证明⑴
《看一看》
1、谁更长
如图,两条线段AB与CD那一条长一些?
观察结果:AB>CD
2、如图,两条线段AB与CD平行吗?
观察结果:AB与CD不平行
测量结果:AB<CD
事实:AB平行CD
新知探究
1、面积相等吗?
如图,长方形草坪中间有一条1m宽的直道.
现准备将其改造成如右图处处1m宽的“曲径”.
两条小道占用草坪的面积相同吗?说说你的理由.
a
b
直道面积:b·1=b
曲径面积:ab-(a-1)b=ab-ab+b=b
∴两条小道占用草坪的面积相同.
平移
a-1
b
新知探究
2、谁大谁小?
已知代数式x2-2x+2及4x-8.
⑴、当x=-5、0、2、3时,分别求出它们的值
⑵、观察上面的结果,你有什么发现?
⑶、能证实你的结论吗?
x
x2-2x+2
4x-8
-5
0
2
3
37
-28
2
-8
2
0
4
5
x2-2x+2>4x-8
x2-2x+2-(4x-8)
=x2-6x+10
=x2-6x+9+1
=(x-3)2+1
求差法
∵
(x-3)2≥0
∴
(x-3)2+1>0
∴
x2-2x+2-(4x-8)>0
∴
x2-2x+2>4x-8
新知探究
3、它们平行吗?
六边形ABCDEF的每一个内角都是相等的,∠1=60°,那么AB与ED,AD与EF有怎样的位置关系?
∵六边形每一个内角都是相等
∴∠F=∠FAB=∠B=∠C=∠CDE=
∵∠1=60°
∴∠2=120°-60°=
60°
∴∠2+∠F=180°
∴AD
∥EF
∵
四边形ABCD
∴∠1+∠B+∠C+∠3=360°
∴∠3=360°-120°-120°-60°=60°
∴∠4=120°-60°=60°
∴∠1=∠4
∴AB∥ED
2
3
4
新知探究
《议一议》在确定上面三个数学结论的正确性时, 我们运用了哪些数学知识?运用了哪些数学方法?
知 识:平移、长方形面积、整式的加减、完全平方公式、非负数、多边形内角和、两直线平行的条件等.
数学方法:平移法、求差法、配方法等.
《读一读》观察、实验、操作中得出的结论还需要运用已学过的数学知识和方法来证明它的正确性.
图(1)
图(1)中有曲线吗?
课堂练习
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
请把图(2)中编号相同的点用线段连接起来.
图(1)
图(2)
图(1)中有曲线吗?
课堂练习
课本149练一练第1、2、3题
下图正中央的两个圆全等吗?
课堂练习
课本149练一练第1、2、3题
数学实验室
《拼一拼》
如图①是一张8㎝×8㎝的正方形纸片.
有人说可将它剪成4块重新拼合,拼成像图②那样长为13,宽为5的长方形.
你认为这可能吗?
不能,因为图①的面积64,而图②的面积为65.
数学实验室
《量一量》
如图,画∠AOB,并画∠AOB的角平分线OC
⑴、将三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别交于点E、F,量一量PE、PF的长度,猜想它们之间有何关系?
⑵、把三角尺绕点P旋转,⑴中的结论还成立吗?
相等
还成立
回顾反思
本节课,我们有哪些收获?
1、仅凭观察、实验、操作得到的结论有时是表面的,片面的,是不够深入,是不够全面的,甚至有时是错误的
2、观察、实验、操作中得出的结论还需要运用已学过的数学知识和方法来证明它的正确性.
3、证明是必要的.
课本154页习题第1、2题
布置作业
课本154页习题第1、2题
谢
谢!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
