青岛版八年级下册 8.2 一元一次不等式 课件 (21张ppt)
文档属性
| 名称 | 青岛版八年级下册 8.2 一元一次不等式 课件 (21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 628.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-23 14:20:27 | ||
图片预览








文档简介
(共21张PPT)
第八章
一元一次不等式
8.2
.1一元一次不等式
1.通过分析实际问题中数量之间的不等关系,抽象出不等式。
2.能在数轴上正确表示出不等式的解集。
什么数的2倍与3的和小于11?
你能用不等式表示出这个问题中的不等关系吗?
观察与思考
不等式
中含有未知数x,它的值不确定,而其他式子中不含有未知数。
通过“估算——检验”,我发现当x=1时,2×1+3<11,这个不等式成立
除x=1外,还有哪些值使这个不等式成立呢?
如果不等式中含有未知数,能使这个不等式成立的未知数的值叫做这个
不等式的解.
不等式的解的概念
不等式的2x+3<11解包括哪些实数呢?
想一想
x
x=
0,
1.5,
-
√2是这个不等式的解
x
x=
4,
5,
6
...
不是这个不等式的解
实际上,满足x<4的任何一个实数都是不等式2x+3<11的解,这样的实数有无数个,
反之,大于或等于4的任何一个实数,都不是这个不等式的解
一个含有未知数的不等式的所有解的集合,叫做这个不等式的解集
。
这个解集还可以用数轴上表示数4的点的左边部分来表示
不等式的解集:
不等式2x+3<11的解集是x<4
这个解集除了用x<4来表示之外,还能用什么来表示?
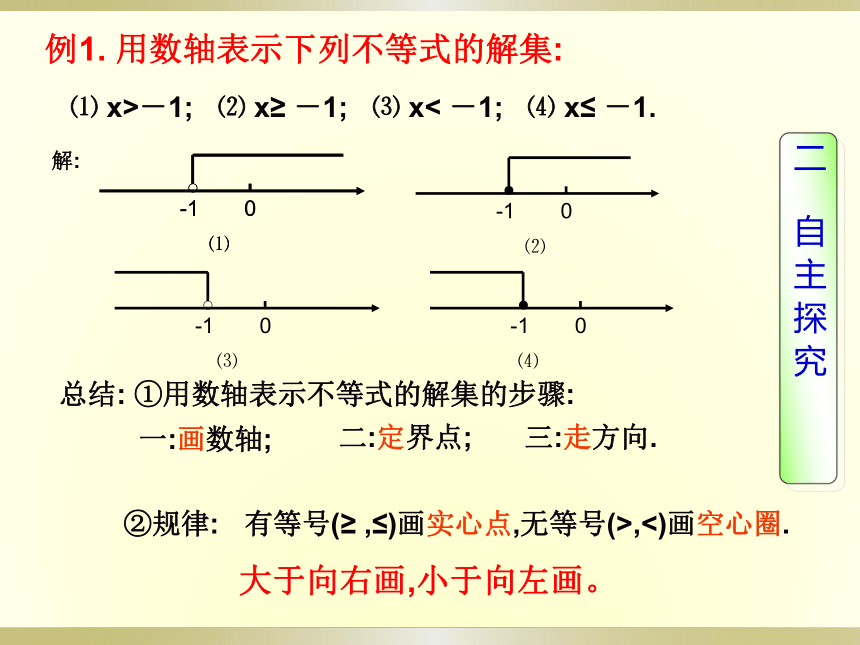
例1.
用数轴表示下列不等式的解集:
⑴
x>-1;
⑵
x≥
-1;
⑶
x<
-1;
⑷
x≤
-1.
解:
○
0
-1
⑴
●
0
-1
⑵
○
0
-1
⑶
●
0
-1
⑷
总结:
①用数轴表示不等式的解集的步骤:
一:画数轴;
二:定界点;
三:走方向.
②规律:
大于向右画,小于向左画。
有等号(≥
,≤)画实心点,无等号(>,<)画空心圈.
二
自
主
探
究
○
0
-1
⑴
在数轴上表示x≥-2正确的是
(
)
-2
A
●
0
-2
B
●
○
0
-2
C
●
0
-2
D
D
火眼金睛
第一种:用式子(如x<4),即用最简形式的不等式(如x>a或x第二种:用数轴,标出数轴上某一区间,其中的点对应的数值都是不等式的解.
不等式解集的表示方法
用不等式表示下列数量关系,再用数轴表示出来:
x小于-1;
x不小于-1;
a是正数;
(4)
b是非负数.
练一练
例2.用不等式表示图中所示的x的不等式的解集.
X<2
X
≤
2
X≥
-7.5
○
0
-3
⑴
○
0
-3
⑶
●
0
2
⑵
●
0
a
⑷
写出下列数轴所表示的不等式的解集:
X
>
-3
X
≥
2
X
<
-3
X
≤
a
火眼金睛
拓展延伸
根据不等式x<2在数轴上表示该解集,有哪些整数解?
有多少个非负整数解?
开放性练习
请你在数轴上表示出不等式x≤3的解集,并找出其中的非负整数解。
解:从图上看出,整数解有无数多个,非负整数解有2个,分别是0、1。
不等式1+x<0的解集在数轴上表示正确的是(
)
A
不等式
这节课你学到了
……
用数轴表示不
等式的解集
不等式的解
不等式的解集
能正确写出数轴表示的不等式的解集
不等式的解
不等式的解集
区别
定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中的一员
解集一定包括了某个解
不等式的解与不等式的解集的区别与联系
1.判断正误:
(1)不等式x-1>0有无数个解;
______________是方程x+4=0的解.
______________是不等式x+4≥0的解
______________是不等式x+4<0的解
×
√
自测一下
自测一下
5、不等式x
<
5的正整数解是
(
)
4
3
2
1
A
C
1.不等式的解的定义。
2.不等式的解集的定义。
通过本课时的学习,我们学习了:
3.用数轴正确表示不等式的解集。
4.正确写出数轴上所表示的不等式的解集。
课堂小结
第八章
一元一次不等式
8.2
.1一元一次不等式
1.通过分析实际问题中数量之间的不等关系,抽象出不等式。
2.能在数轴上正确表示出不等式的解集。
什么数的2倍与3的和小于11?
你能用不等式表示出这个问题中的不等关系吗?
观察与思考
不等式
中含有未知数x,它的值不确定,而其他式子中不含有未知数。
通过“估算——检验”,我发现当x=1时,2×1+3<11,这个不等式成立
除x=1外,还有哪些值使这个不等式成立呢?
如果不等式中含有未知数,能使这个不等式成立的未知数的值叫做这个
不等式的解.
不等式的解的概念
不等式的2x+3<11解包括哪些实数呢?
想一想
x
x=
0,
1.5,
-
√2是这个不等式的解
x
x=
4,
5,
6
...
不是这个不等式的解
实际上,满足x<4的任何一个实数都是不等式2x+3<11的解,这样的实数有无数个,
反之,大于或等于4的任何一个实数,都不是这个不等式的解
一个含有未知数的不等式的所有解的集合,叫做这个不等式的解集
。
这个解集还可以用数轴上表示数4的点的左边部分来表示
不等式的解集:
不等式2x+3<11的解集是x<4
这个解集除了用x<4来表示之外,还能用什么来表示?
例1.
用数轴表示下列不等式的解集:
⑴
x>-1;
⑵
x≥
-1;
⑶
x<
-1;
⑷
x≤
-1.
解:
○
0
-1
⑴
●
0
-1
⑵
○
0
-1
⑶
●
0
-1
⑷
总结:
①用数轴表示不等式的解集的步骤:
一:画数轴;
二:定界点;
三:走方向.
②规律:
大于向右画,小于向左画。
有等号(≥
,≤)画实心点,无等号(>,<)画空心圈.
二
自
主
探
究
○
0
-1
⑴
在数轴上表示x≥-2正确的是
(
)
-2
A
●
0
-2
B
●
○
0
-2
C
●
0
-2
D
D
火眼金睛
第一种:用式子(如x<4),即用最简形式的不等式(如x>a或x
不等式解集的表示方法
用不等式表示下列数量关系,再用数轴表示出来:
x小于-1;
x不小于-1;
a是正数;
(4)
b是非负数.
练一练
例2.用不等式表示图中所示的x的不等式的解集.
X<2
X
≤
2
X≥
-7.5
○
0
-3
⑴
○
0
-3
⑶
●
0
2
⑵
●
0
a
⑷
写出下列数轴所表示的不等式的解集:
X
>
-3
X
≥
2
X
<
-3
X
≤
a
火眼金睛
拓展延伸
根据不等式x<2在数轴上表示该解集,有哪些整数解?
有多少个非负整数解?
开放性练习
请你在数轴上表示出不等式x≤3的解集,并找出其中的非负整数解。
解:从图上看出,整数解有无数多个,非负整数解有2个,分别是0、1。
不等式1+x<0的解集在数轴上表示正确的是(
)
A
不等式
这节课你学到了
……
用数轴表示不
等式的解集
不等式的解
不等式的解集
能正确写出数轴表示的不等式的解集
不等式的解
不等式的解集
区别
定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中的一员
解集一定包括了某个解
不等式的解与不等式的解集的区别与联系
1.判断正误:
(1)不等式x-1>0有无数个解;
______________是方程x+4=0的解.
______________是不等式x+4≥0的解
______________是不等式x+4<0的解
×
√
自测一下
自测一下
5、不等式x
<
5的正整数解是
(
)
4
3
2
1
A
C
1.不等式的解的定义。
2.不等式的解集的定义。
通过本课时的学习,我们学习了:
3.用数轴正确表示不等式的解集。
4.正确写出数轴上所表示的不等式的解集。
课堂小结
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
