零指数幂与负整指数幂(一)课件
图片预览





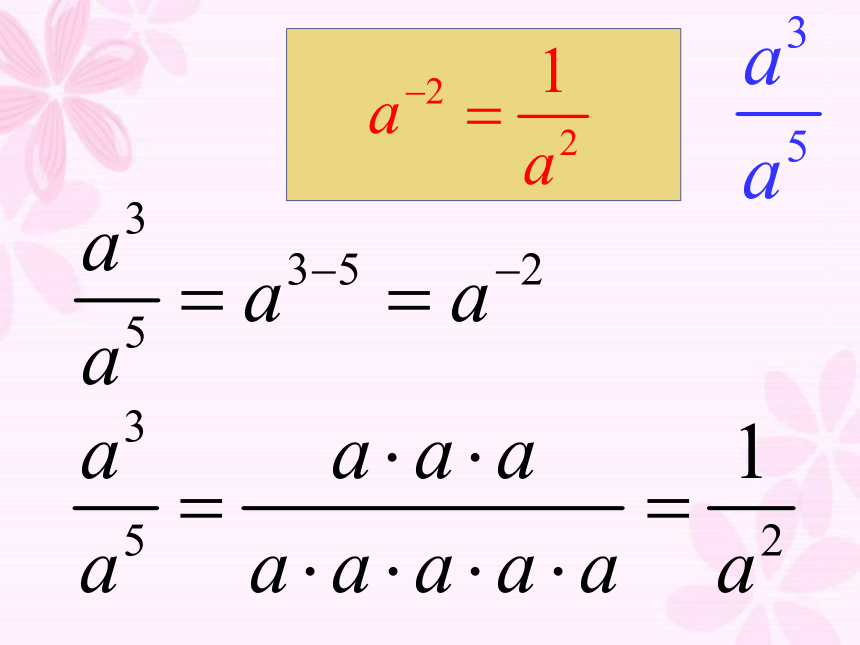

文档简介
(共17张PPT)
幂的运算法则
m,n为正整数
复习回顾
思考:
法则4.
(m,n为正整数)
规定
任何不等于零的数的零次幂都等于1
规定
任何不等于零的数的 (n为正整数)次幂,等于这个数的n次幂的倒数
例1 计算:
运算法则
(m,n为整数a 0,)
练一练
例2.如果代数式 有意义,
求x的取值范围。
解:
1、下列计算对吗?为什么? 错的请改正。
①(-3)0=-1; ②(-2)-1=1;③ 2-2=-4;
④a3÷a3=0; ⑤ ap·a-p =1(a≠0)。
随堂练习
2 、计算下列各式,并把结果化为只含有正整数指数幂的形式:
(1)(a-3)2(ab2)-3; (2)(2mn2)-2(m-2n-1)-3;
(3)(x-3yz-2)2; (4)(a3b-1)-2(a-2b2)2;
(5)(2m2n-3)3(-mn-2)-2。
随堂练习
3、计算:
(1) 10-2 ; (2) 2-2 ; (3) ; (4)4-2;
(5)10-3; (6)(-0.5)-3; (7)(-3)-4; (8) ;
(9) ; (10)810÷810; (11)102÷105;
(12) ;(13)510÷254。
随堂练习
小结
2.同底数幂的除法法则
am ÷an = a m-n (a≠0,m、n都是正整数,且m>n)中的条件可以改为:
(a≠0,m、n都是整数)
1.我们知道了指数有正整数,还有负整数、零 。
a0 =1,(a≠0),
( a≠0 ,且n为正整数)
幂的运算法则
m,n为正整数
复习回顾
思考:
法则4.
(m,n为正整数)
规定
任何不等于零的数的零次幂都等于1
规定
任何不等于零的数的 (n为正整数)次幂,等于这个数的n次幂的倒数
例1 计算:
运算法则
(m,n为整数a 0,)
练一练
例2.如果代数式 有意义,
求x的取值范围。
解:
1、下列计算对吗?为什么? 错的请改正。
①(-3)0=-1; ②(-2)-1=1;③ 2-2=-4;
④a3÷a3=0; ⑤ ap·a-p =1(a≠0)。
随堂练习
2 、计算下列各式,并把结果化为只含有正整数指数幂的形式:
(1)(a-3)2(ab2)-3; (2)(2mn2)-2(m-2n-1)-3;
(3)(x-3yz-2)2; (4)(a3b-1)-2(a-2b2)2;
(5)(2m2n-3)3(-mn-2)-2。
随堂练习
3、计算:
(1) 10-2 ; (2) 2-2 ; (3) ; (4)4-2;
(5)10-3; (6)(-0.5)-3; (7)(-3)-4; (8) ;
(9) ; (10)810÷810; (11)102÷105;
(12) ;(13)510÷254。
随堂练习
小结
2.同底数幂的除法法则
am ÷an = a m-n (a≠0,m、n都是正整数,且m>n)中的条件可以改为:
(a≠0,m、n都是整数)
1.我们知道了指数有正整数,还有负整数、零 。
a0 =1,(a≠0),
( a≠0 ,且n为正整数)
