4.2 图形的全等 课件(共26张PPT)
文档属性
| 名称 | 4.2 图形的全等 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-22 13:38:41 | ||
图片预览





文档简介
第2节 图形的全等
第四章 三角形
2021年春北师大版七年级数学下册
1 了解全等形的概念,会判断两个图形是不是全等形.
2 理解全等三角形的概念,能识别全等三角形中的对应边、对应角.(难点)
3 掌握全等三角形的性质,能利用全等三角形的性质解决相关问题.(重点)
学习目标
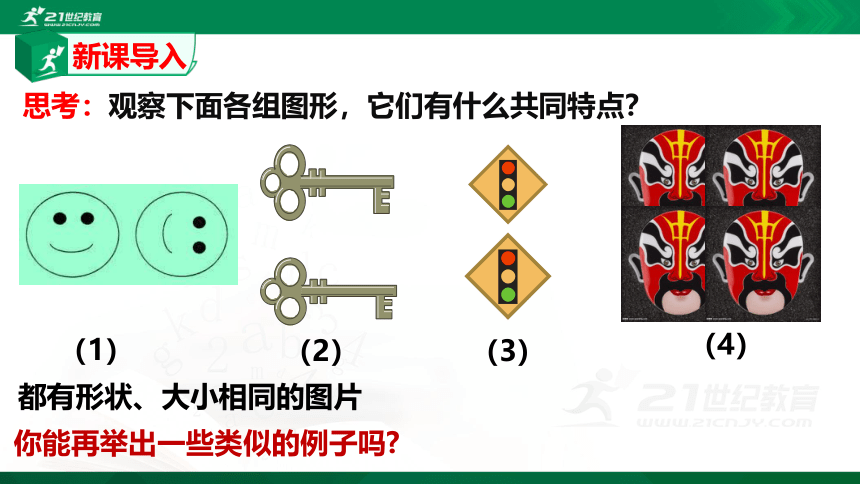
思考:观察下面各组图形,它们有什么共同特点?
(1)
(2)
(3)
(4)
都有形状、大小相同的图片
你能再举出一些类似的例子吗?
新课导入
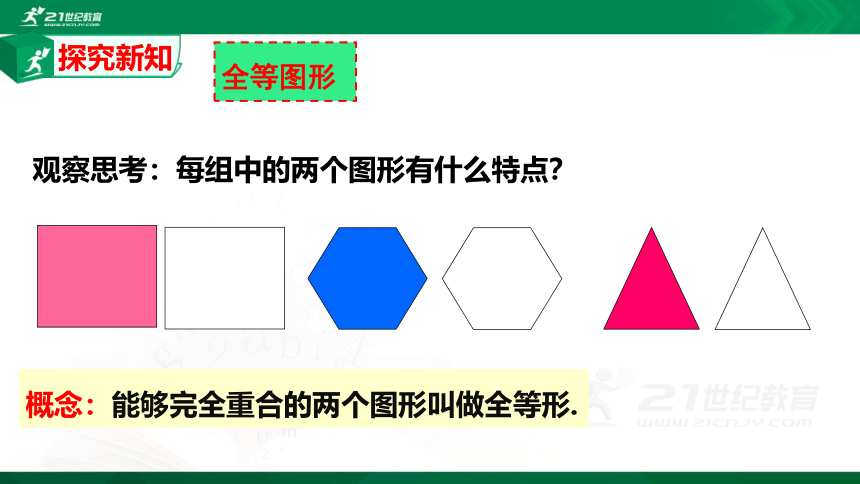
全等图形
观察思考:每组中的两个图形有什么特点?
概念:能够完全重合的两个图形叫做全等形.
探究新知
一个图形经过平移,翻折,旋转后,位置变化了,但 和
都没有改变,即平移,翻折,旋转前后的图形_________ .
完全重合
形状
大小
定义:形状、大小相同的图形放在一起能够完全重合.
能够完全重合的两个图形叫做全等图形.
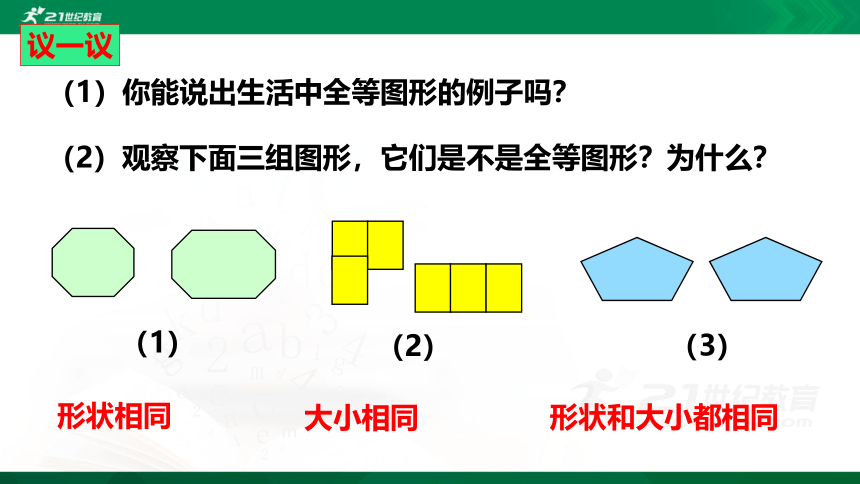
议一议
(1)你能说出生活中全等图形的例子吗?
(2)观察下面三组图形,它们是不是全等图形?为什么?
(2)
(1)
(3)
形状相同
大小相同
形状和大小都相同
(3)如果两个图形全等,它们的形状和大小一定都相同吗?
全等图形的形状和大小都相同.
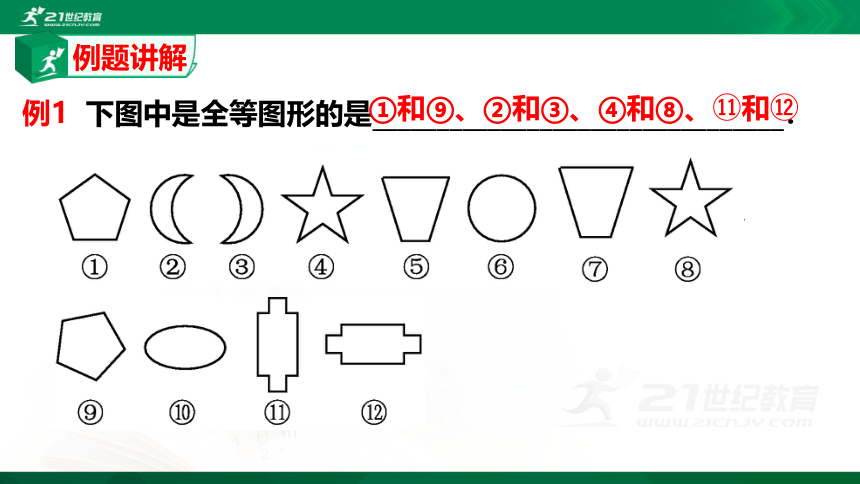
例1
下图中是全等图形的是________________________________.
①和⑨、②和③、④和⑧、?和?
例题讲解
A
B
C
E
D
F
例如
1 三角形全等定义:能够完全重合的两个三角形,叫做____________.
全等三角形
A
B
C
A(D)
B(E)
C(F)
D
E
F
顶点 A,D 重合,它们是对应顶点;
AB 边与 DE 边重合,它们是对应边;
∠A 与 ∠D 重合,它们是对应角.
2 表示方法:全等用符号“≌”表示,读作“全等于”.记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
△ABC≌△FDE
全等三角形的对应边相等,对应角相等.
∵△ABC≌△DEF,
∴AB=DE,AC=DF ,BC=EF,(全等三角形的对应边相等)
∠A=∠F,∠B=∠D,∠C=∠E.(全等三角形的对应角相等)
几何语言:
例2 如图:△AOD≌△BOC,写出其中相等的角
A
D
C
B
O
解:∠A=∠B
∠D=∠C
∠DOA=∠COB
例题讲解
例3 如图,Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B,C,D三点在一条直线上,求∠ACE的度数.
例题讲解
解:因为Rt△ABC≌Rt△CDE,
所以∠BAC=∠DCE.
又因为在Rt△ABC中,∠B=90°,
所以∠ACB+∠BAC=90°.
所以∠ACB+∠ECD=90°.
所以∠ACE=180°-(∠ACB+∠ECD)
=180°-90°
=90°.
议一议
(1)全等三角形对应边的高相等吗?对应边的中线呢?还有哪些相等的线段?举例说明.
全等三角形对应边的高、中线、角平分线分别相等.
A
B
C
C′
B′
A′
(2)如图所示,已知 △ABC ≌ △A′B′C′ ,你如何在 △A′B′C′ 中画出与线段 DE 相对应的线段?
在B′C′边上取B′D′ = BD,在 B′A′ 边上取 B′E′ = BE,连接D′E′.
A
B
C
D
E
A′
B′
C′
D′
E′
做一做
如图所示,一个等边三角形,你能把它分成两个全等的三角形吗?三个呢?四个呢?
1 下列说法中正确的有( )
①用一张底片冲洗出来的10张1寸相片是全等图形;
②我国国旗上的4颗小五角星是全等图形;
③所有的正方形是全等图形;
④全等图形的面积一定相等.
A.1个 B.2个 C.3个 D.4个
课堂练习
2 下列四组图形中,是全等图形的一组是( )
3 如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B
=________.
4 如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是( )
A.∠1=∠2
B.∠ACB=∠DAC
C.AB=AD
D.∠B=∠D
5 如图,若△ABC≌△EFC,且CF=3cm,∠EFC=64°,则BC=_____cm,∠B=_____.
B
A
E
F
C
全等三角形
全等图形:能够完全重合的两个图形叫做全等形
全等三角形:能够完全重合的两个三角形叫做全等三角形
全等三角形的性质
全等三角形的对应边相等
全等三角形的对应角相等
2 全等三角形的性质的作用:
(1)求角的度数;(2)说明两个角相等;(3)求线段的长度;(4)说明两条线段相等;(5)判断两条直线的位置关系等.
课堂小结
谢谢聆听
第四章 三角形
2021年春北师大版七年级数学下册
1 了解全等形的概念,会判断两个图形是不是全等形.
2 理解全等三角形的概念,能识别全等三角形中的对应边、对应角.(难点)
3 掌握全等三角形的性质,能利用全等三角形的性质解决相关问题.(重点)
学习目标
思考:观察下面各组图形,它们有什么共同特点?
(1)
(2)
(3)
(4)
都有形状、大小相同的图片
你能再举出一些类似的例子吗?
新课导入
全等图形
观察思考:每组中的两个图形有什么特点?
概念:能够完全重合的两个图形叫做全等形.
探究新知
一个图形经过平移,翻折,旋转后,位置变化了,但 和
都没有改变,即平移,翻折,旋转前后的图形_________ .
完全重合
形状
大小
定义:形状、大小相同的图形放在一起能够完全重合.
能够完全重合的两个图形叫做全等图形.
议一议
(1)你能说出生活中全等图形的例子吗?
(2)观察下面三组图形,它们是不是全等图形?为什么?
(2)
(1)
(3)
形状相同
大小相同
形状和大小都相同
(3)如果两个图形全等,它们的形状和大小一定都相同吗?
全等图形的形状和大小都相同.
例1
下图中是全等图形的是________________________________.
①和⑨、②和③、④和⑧、?和?
例题讲解
A
B
C
E
D
F
例如
1 三角形全等定义:能够完全重合的两个三角形,叫做____________.
全等三角形
A
B
C
A(D)
B(E)
C(F)
D
E
F
顶点 A,D 重合,它们是对应顶点;
AB 边与 DE 边重合,它们是对应边;
∠A 与 ∠D 重合,它们是对应角.
2 表示方法:全等用符号“≌”表示,读作“全等于”.记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
△ABC≌△FDE
全等三角形的对应边相等,对应角相等.
∵△ABC≌△DEF,
∴AB=DE,AC=DF ,BC=EF,(全等三角形的对应边相等)
∠A=∠F,∠B=∠D,∠C=∠E.(全等三角形的对应角相等)
几何语言:
例2 如图:△AOD≌△BOC,写出其中相等的角
A
D
C
B
O
解:∠A=∠B
∠D=∠C
∠DOA=∠COB
例题讲解
例3 如图,Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B,C,D三点在一条直线上,求∠ACE的度数.
例题讲解
解:因为Rt△ABC≌Rt△CDE,
所以∠BAC=∠DCE.
又因为在Rt△ABC中,∠B=90°,
所以∠ACB+∠BAC=90°.
所以∠ACB+∠ECD=90°.
所以∠ACE=180°-(∠ACB+∠ECD)
=180°-90°
=90°.
议一议
(1)全等三角形对应边的高相等吗?对应边的中线呢?还有哪些相等的线段?举例说明.
全等三角形对应边的高、中线、角平分线分别相等.
A
B
C
C′
B′
A′
(2)如图所示,已知 △ABC ≌ △A′B′C′ ,你如何在 △A′B′C′ 中画出与线段 DE 相对应的线段?
在B′C′边上取B′D′ = BD,在 B′A′ 边上取 B′E′ = BE,连接D′E′.
A
B
C
D
E
A′
B′
C′
D′
E′
做一做
如图所示,一个等边三角形,你能把它分成两个全等的三角形吗?三个呢?四个呢?
1 下列说法中正确的有( )
①用一张底片冲洗出来的10张1寸相片是全等图形;
②我国国旗上的4颗小五角星是全等图形;
③所有的正方形是全等图形;
④全等图形的面积一定相等.
A.1个 B.2个 C.3个 D.4个
课堂练习
2 下列四组图形中,是全等图形的一组是( )
3 如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B
=________.
4 如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是( )
A.∠1=∠2
B.∠ACB=∠DAC
C.AB=AD
D.∠B=∠D
5 如图,若△ABC≌△EFC,且CF=3cm,∠EFC=64°,则BC=_____cm,∠B=_____.
B
A
E
F
C
全等三角形
全等图形:能够完全重合的两个图形叫做全等形
全等三角形:能够完全重合的两个三角形叫做全等三角形
全等三角形的性质
全等三角形的对应边相等
全等三角形的对应角相等
2 全等三角形的性质的作用:
(1)求角的度数;(2)说明两个角相等;(3)求线段的长度;(4)说明两条线段相等;(5)判断两条直线的位置关系等.
课堂小结
谢谢聆听
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
