2.2.4 平面与平面平行的性质 课件(共19张PPT)—2020-2021学年高一人教A版数学必修二第二章
文档属性
| 名称 | 2.2.4 平面与平面平行的性质 课件(共19张PPT)—2020-2021学年高一人教A版数学必修二第二章 |

|
|
| 格式 | ppt | ||
| 文件大小 | 415.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-22 21:04:50 | ||
图片预览



文档简介
(共19张PPT)
问题提出
1、什么叫两平面平行?
如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面平行.
2、两平面平行的判定定理是什么?
3、两平面平行的判定定理解决了两平面平行的条件;反之,在两平面平行的条件下,会得到什么结论?
问题讨论
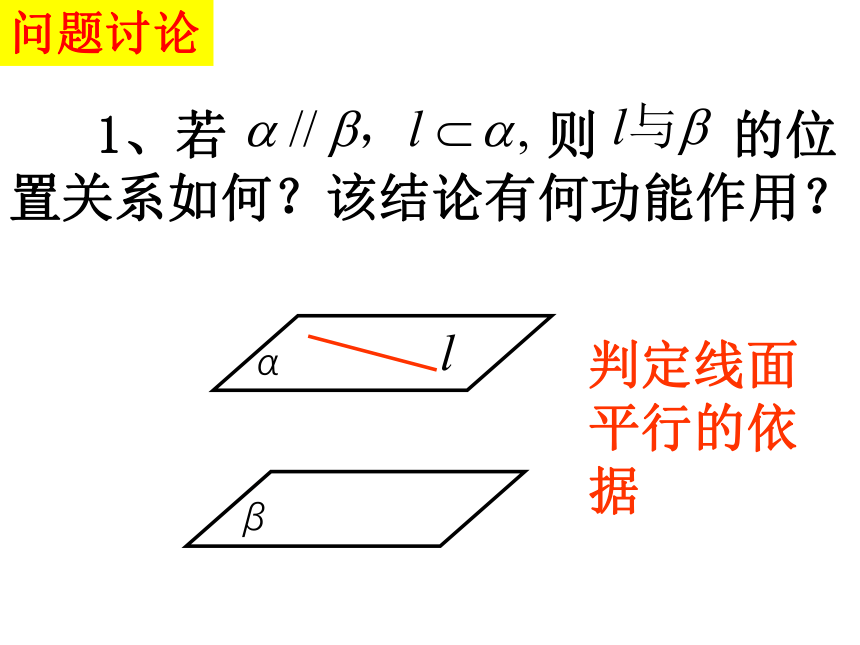
1、若
则
的位置关系如何?该结论有何功能作用?
β
α
判定线面平行的依据
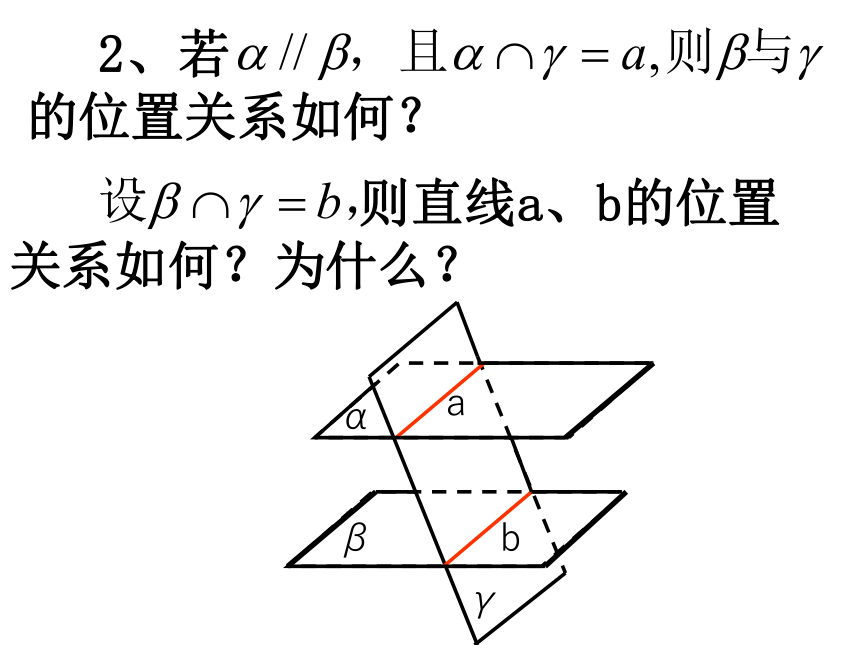
2、若
的位置关系如何?
则直线a、b的位置关系如何?为什么?
β
α
γ
a
b
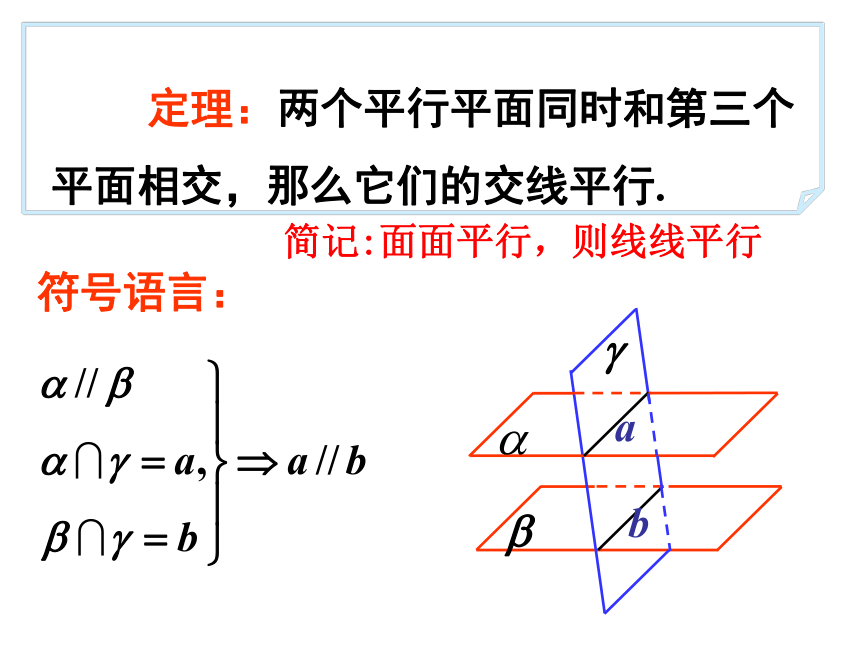
定理:两个平行平面同时和第三个
平面相交,那么它们的交线平行.
符号语言:
b
a
简记:面面平行,则线线平行
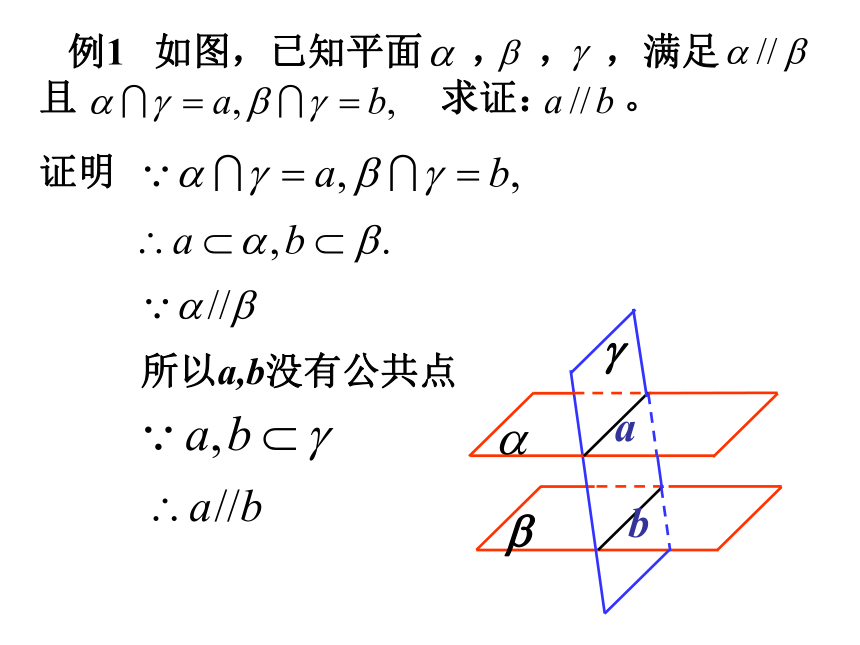
例1
如图,已知平面
,
,
,满足
且
求证:
。
证明
所以a,b没有公共点
b
a
2、若两个平面互相平行,则其中一个平面
中的直线必平行于另一个平面;
3、平行于同一平面的两平面平行;
4、过平面外一点有且只有一个平面与这
个平面平行;
5、夹在两平行平面间的平行线段相等。
面面平行的其它一些性质
且AC∥BD,则AC与BD的长度关系如何?
β
α
A
D
C
B
过点A作直线
β
α
A
7、如果平面α、β都与平面γ相交,且交线平行,则α∥β吗?
b
α
β
γ
a
8
如图,设AB、CD为夹在两个平行平面
、
之间
的线段,且直线AB、CD为异面直线,M、P
分别为AB、CD
的中点,
求证:
直线MP
//
平面
.
取AE的中点为N,
提示:过A做CD的平行直线交
于E,
连结BE,ED,BD,MN,MP,NP
1.
若?∥?,?∥?,求证:
?∥?
.
练习
a
b
?
?
?
b'
a'
N
M
O
an
bn
例2
P是长方形ABCD所在平面外的一点,AB、PD两点M、N满足AM:MB=ND:NP。
求证:MN∥平面PBC。
P
N
M
D
C
B
A
E
H
O
例3、已知ABCD是平行四边形,点P是平面ABCD
外一点,M是PC的中点,在DM上取一点G,
画出过G和AP的平面。
A
C
B
D
G
P
M
练习:
点P在平面VAC内,画出过点P作一个截面平行于直线VB和AC。
V
A
C
B
P
F
E
G
H
例4
如图:a∥α,A是α另一侧的点,B、C、D
是α上的点
,线段AB、AC、AD交于E、F、G
点,若BD=4,CF=4,AF=5,求EG.
α
a
A
C
B
D
E
G
F
课外作业:
1、已知α∥β,AB交α、β于A、B,CD交
α、β于C、D,AB∩CD=S,AS=8,BS=9,
CD=34,求SC。
α
β
A
D
C
B
S
α
β
C
B
S
A
D
A1
B1
C1
D1
A
B
C
D
2、已知P、Q是边长为1的正方体ABCD-A1B1C1D1
的面AA1DD1
、面ABCD的中心
(1)求证:PQ//
平面DD1C1C
(2)求线段的PQ长
P
Q
问题提出
1、什么叫两平面平行?
如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面平行.
2、两平面平行的判定定理是什么?
3、两平面平行的判定定理解决了两平面平行的条件;反之,在两平面平行的条件下,会得到什么结论?
问题讨论
1、若
则
的位置关系如何?该结论有何功能作用?
β
α
判定线面平行的依据
2、若
的位置关系如何?
则直线a、b的位置关系如何?为什么?
β
α
γ
a
b
定理:两个平行平面同时和第三个
平面相交,那么它们的交线平行.
符号语言:
b
a
简记:面面平行,则线线平行
例1
如图,已知平面
,
,
,满足
且
求证:
。
证明
所以a,b没有公共点
b
a
2、若两个平面互相平行,则其中一个平面
中的直线必平行于另一个平面;
3、平行于同一平面的两平面平行;
4、过平面外一点有且只有一个平面与这
个平面平行;
5、夹在两平行平面间的平行线段相等。
面面平行的其它一些性质
且AC∥BD,则AC与BD的长度关系如何?
β
α
A
D
C
B
过点A作直线
β
α
A
7、如果平面α、β都与平面γ相交,且交线平行,则α∥β吗?
b
α
β
γ
a
8
如图,设AB、CD为夹在两个平行平面
、
之间
的线段,且直线AB、CD为异面直线,M、P
分别为AB、CD
的中点,
求证:
直线MP
//
平面
.
取AE的中点为N,
提示:过A做CD的平行直线交
于E,
连结BE,ED,BD,MN,MP,NP
1.
若?∥?,?∥?,求证:
?∥?
.
练习
a
b
?
?
?
b'
a'
N
M
O
an
bn
例2
P是长方形ABCD所在平面外的一点,AB、PD两点M、N满足AM:MB=ND:NP。
求证:MN∥平面PBC。
P
N
M
D
C
B
A
E
H
O
例3、已知ABCD是平行四边形,点P是平面ABCD
外一点,M是PC的中点,在DM上取一点G,
画出过G和AP的平面。
A
C
B
D
G
P
M
练习:
点P在平面VAC内,画出过点P作一个截面平行于直线VB和AC。
V
A
C
B
P
F
E
G
H
例4
如图:a∥α,A是α另一侧的点,B、C、D
是α上的点
,线段AB、AC、AD交于E、F、G
点,若BD=4,CF=4,AF=5,求EG.
α
a
A
C
B
D
E
G
F
课外作业:
1、已知α∥β,AB交α、β于A、B,CD交
α、β于C、D,AB∩CD=S,AS=8,BS=9,
CD=34,求SC。
α
β
A
D
C
B
S
α
β
C
B
S
A
D
A1
B1
C1
D1
A
B
C
D
2、已知P、Q是边长为1的正方体ABCD-A1B1C1D1
的面AA1DD1
、面ABCD的中心
(1)求证:PQ//
平面DD1C1C
(2)求线段的PQ长
P
Q
