数学人教A版(2019) 选择性必修第三册 6.3.2 二项式系数的性质(共18张PPT)
文档属性
| 名称 | 数学人教A版(2019) 选择性必修第三册 6.3.2 二项式系数的性质(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 591.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-22 21:06:14 | ||
图片预览






文档简介
(共18张PPT)
6.3.2
二项式系数的性质
新知导入
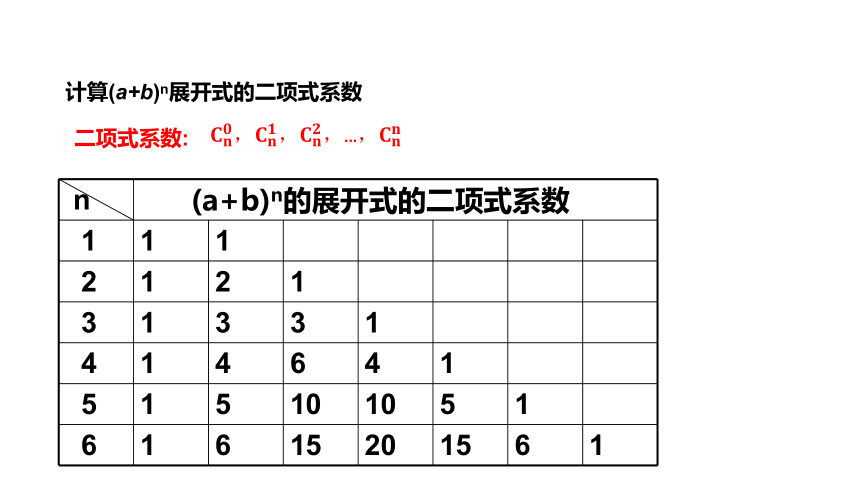
计算(a+b)n展开式的二项式系数
二项式系数:
,,,...,
n
(a+b)n的展开式的二项式系数
1
1
1
2
1
2
1
3
1
3
3
1
4
1
4
6
4
1
5
1
5
10
10
5
1
6
1
6
15
20
15
6
1
新知导入
将上表写成如下形式:
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
新知导入
思考:通过上表和上图,能发现什么规律?
在同一行中,每行两端都是1,与这两个1等距离的项的系数相等,
即每一行都具有对称性.
在相邻的两行中,除了开头和结尾的两个数外,其他每个数都等于它肩上两个数之和.
第n(n∈N
)行的各数之和为2n
当n=2,4,6时,中间一项值最大;当n=1,3,5时,中间两项值最大.
.
新知讲解
二项式系数的性质
(1)对称性
与首末两端“等距离”的两个二项式系数相等,这一性质可直接由公式得到,对称轴为r=n/2
(2)增减性与最大值
因为
即,由
当
时,
二项式系数是逐渐增大的,由对称性可知,
它的后半部分是逐渐减小的.
新知讲解
当n是偶数时,中间的一项取得最大值.
当n是奇数时,中间的两项和相等,且同时取得最大值.
(3)各二项式系数的和
已知
(1+x)n
=
令x=1
得(1+1)n=
所以,(a+b)n的展开式的各二项式系数之和为2n
例题讲解
例1
求证:在(a+b)n
的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
证明:在展开式
(a+b)n=中,
令a=1,b=-1,得
(
1-1
)n=
即
因此
即在(a+b)n
的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
例题讲解
例2
在二项式(2x-3y)9的展开式中,求:
(1)二项式系数之和.
(2)各项系数之和.
(3)所有奇数项系数之和.
解:设(2x-3y)9=a0x9+a1x8y+a2x7y2+…+a9y9.
(1)二项式系数之和为:.
(2)各项系数之和为:a0+a1+a2+…+a9,
令x=1,y=1,所以a0+a1+a2+…+a9=(2-3)9=-1.
(3)令x=1,y=-1,可得a0-a1+a2-…-a9=59,
又a0+a1+a2+…+a9=-1,将两式相加得a0+a2+a4+a6+a8=(59-1)/2,
则所有奇数项系数之和为(59-1)/2.
例题讲解
例3
在的展开式中
(1)求二项式系数最大的项;
(2)系数的绝对值最大的项是第几项?
解:展开式的通项公式为
(1)二项式系数最大的项为中间项,即为第5项,因此
(2)设第k+1项系数的绝对值最大,则,即
解得k=5或k=6,故系数绝对值最大的项是第6项或第7项.
课堂练习
2.已知的展开式中,各项系数的和与其各项二项式系数的和之比为64,则
(
)
A.4
B.5
C.6
D.7
C
1.展开式中各项系数之和为(
)
A.26
B.36C.46
D.1
A
3.的展开式中系数最大的项为(
)
A.第4项
B.第5项
C.第7项
D.第8项
B
课堂练习
4.
已知的展开式中所有项的系数和等于,则展开式中项的系数的最大值是(
)
A.
B.
C.7
D.70
C
5.的展开式中,系数最大的项是
(
)
A.第项
B.第n项
C.第n+1项
D.第n项与第n+1项
C
6.
若(1+x)3(1-2x)4=a0+a1x+a2x2+...+a7x7
,则a0+a2+a4+a6=
(
)
A.3
B.4
C.5
D.6
B
课堂练习
7.已知(2m+x)(1+x)4的展开式中x的奇数次幂项的系数之和为64,
则m=(
)
A.
B.
C.4
D.
7
B
拓展提高
8.
设
(1-x)15=a0+
a1x+
a2x2+...+
a15x15
求:
(1)
a1+
a2+
a3+
a4+...+
a15
(2)
a1+
a3+
a5+...+
a15
解:(1)令x=0可得115=a0,则a0=1
令x=1可得015=a0+a1+a2+...+a15,
所以
a1+a2+...+a15=-a0=-1.
(2)令x=-1
可得
215=a0-a1+a2-a3+...-a15
①
令x=1
可得
015=a0+a1+a2+a3+...+a15
②
①-②
得:215=-2(a1+a3+a5+...+a15
)
所以a1+a3+a5+...+a15=-214.
拓展提高
9.在
的展开式中.
求:(1)所有项的系数和;
(2)x4的系数;
(3)系数最大的项.
解:(1)令x=1
,该展开式中所有项的系数和为312
(2)
该展开式的通项公式为:
令36-4k=4,解得k=8,所以x4的系数为
(3)
设第k+1(r∈N,k≤12)项的系数最大,则
解得,因为k∈N,所以k=4
所以该展开式中系数最大的项为
链接高考
10.(2011
全国高考真题(理))的展开式中各项系数的和为2,则该展开式中常数项为(
)
A.-40
B.-20
C.20
D.40
D
11.
(2020
北京高考真题)在的展开式中,x2的系数为(
).
A.-5
B.5
C.-10
D.10
C
链接高考
12.(2018
全国高考真题(理))的展开式中x4的系数为(
)
A.10
B.20
C.40
D.80
13.(2020
天津高考真题)在的展开式中,x2的系数是_________.
10
C
14.(2020
全国高考真题(理))的展开式中常数项是__________(用数字作答).
240
课堂总结
(1)对称性
(2)增减性与最大值
(3)各二项式系数的和
1、二项式系数的性质
板书设计
6.3.2
二项式系数的性质
一、新知导入
二、新知讲解
二项式系数的性质
三、例题讲解
四、课堂练习
五、拓展提高
六、课堂总结
七、作业布置
6.3.2
二项式系数的性质
新知导入
计算(a+b)n展开式的二项式系数
二项式系数:
,,,...,
n
(a+b)n的展开式的二项式系数
1
1
1
2
1
2
1
3
1
3
3
1
4
1
4
6
4
1
5
1
5
10
10
5
1
6
1
6
15
20
15
6
1
新知导入
将上表写成如下形式:
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
新知导入
思考:通过上表和上图,能发现什么规律?
在同一行中,每行两端都是1,与这两个1等距离的项的系数相等,
即每一行都具有对称性.
在相邻的两行中,除了开头和结尾的两个数外,其他每个数都等于它肩上两个数之和.
第n(n∈N
)行的各数之和为2n
当n=2,4,6时,中间一项值最大;当n=1,3,5时,中间两项值最大.
.
新知讲解
二项式系数的性质
(1)对称性
与首末两端“等距离”的两个二项式系数相等,这一性质可直接由公式得到,对称轴为r=n/2
(2)增减性与最大值
因为
即,由
当
时,
二项式系数是逐渐增大的,由对称性可知,
它的后半部分是逐渐减小的.
新知讲解
当n是偶数时,中间的一项取得最大值.
当n是奇数时,中间的两项和相等,且同时取得最大值.
(3)各二项式系数的和
已知
(1+x)n
=
令x=1
得(1+1)n=
所以,(a+b)n的展开式的各二项式系数之和为2n
例题讲解
例1
求证:在(a+b)n
的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
证明:在展开式
(a+b)n=中,
令a=1,b=-1,得
(
1-1
)n=
即
因此
即在(a+b)n
的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
例题讲解
例2
在二项式(2x-3y)9的展开式中,求:
(1)二项式系数之和.
(2)各项系数之和.
(3)所有奇数项系数之和.
解:设(2x-3y)9=a0x9+a1x8y+a2x7y2+…+a9y9.
(1)二项式系数之和为:.
(2)各项系数之和为:a0+a1+a2+…+a9,
令x=1,y=1,所以a0+a1+a2+…+a9=(2-3)9=-1.
(3)令x=1,y=-1,可得a0-a1+a2-…-a9=59,
又a0+a1+a2+…+a9=-1,将两式相加得a0+a2+a4+a6+a8=(59-1)/2,
则所有奇数项系数之和为(59-1)/2.
例题讲解
例3
在的展开式中
(1)求二项式系数最大的项;
(2)系数的绝对值最大的项是第几项?
解:展开式的通项公式为
(1)二项式系数最大的项为中间项,即为第5项,因此
(2)设第k+1项系数的绝对值最大,则,即
解得k=5或k=6,故系数绝对值最大的项是第6项或第7项.
课堂练习
2.已知的展开式中,各项系数的和与其各项二项式系数的和之比为64,则
(
)
A.4
B.5
C.6
D.7
C
1.展开式中各项系数之和为(
)
A.26
B.36C.46
D.1
A
3.的展开式中系数最大的项为(
)
A.第4项
B.第5项
C.第7项
D.第8项
B
课堂练习
4.
已知的展开式中所有项的系数和等于,则展开式中项的系数的最大值是(
)
A.
B.
C.7
D.70
C
5.的展开式中,系数最大的项是
(
)
A.第项
B.第n项
C.第n+1项
D.第n项与第n+1项
C
6.
若(1+x)3(1-2x)4=a0+a1x+a2x2+...+a7x7
,则a0+a2+a4+a6=
(
)
A.3
B.4
C.5
D.6
B
课堂练习
7.已知(2m+x)(1+x)4的展开式中x的奇数次幂项的系数之和为64,
则m=(
)
A.
B.
C.4
D.
7
B
拓展提高
8.
设
(1-x)15=a0+
a1x+
a2x2+...+
a15x15
求:
(1)
a1+
a2+
a3+
a4+...+
a15
(2)
a1+
a3+
a5+...+
a15
解:(1)令x=0可得115=a0,则a0=1
令x=1可得015=a0+a1+a2+...+a15,
所以
a1+a2+...+a15=-a0=-1.
(2)令x=-1
可得
215=a0-a1+a2-a3+...-a15
①
令x=1
可得
015=a0+a1+a2+a3+...+a15
②
①-②
得:215=-2(a1+a3+a5+...+a15
)
所以a1+a3+a5+...+a15=-214.
拓展提高
9.在
的展开式中.
求:(1)所有项的系数和;
(2)x4的系数;
(3)系数最大的项.
解:(1)令x=1
,该展开式中所有项的系数和为312
(2)
该展开式的通项公式为:
令36-4k=4,解得k=8,所以x4的系数为
(3)
设第k+1(r∈N,k≤12)项的系数最大,则
解得,因为k∈N,所以k=4
所以该展开式中系数最大的项为
链接高考
10.(2011
全国高考真题(理))的展开式中各项系数的和为2,则该展开式中常数项为(
)
A.-40
B.-20
C.20
D.40
D
11.
(2020
北京高考真题)在的展开式中,x2的系数为(
).
A.-5
B.5
C.-10
D.10
C
链接高考
12.(2018
全国高考真题(理))的展开式中x4的系数为(
)
A.10
B.20
C.40
D.80
13.(2020
天津高考真题)在的展开式中,x2的系数是_________.
10
C
14.(2020
全国高考真题(理))的展开式中常数项是__________(用数字作答).
240
课堂总结
(1)对称性
(2)增减性与最大值
(3)各二项式系数的和
1、二项式系数的性质
板书设计
6.3.2
二项式系数的性质
一、新知导入
二、新知讲解
二项式系数的性质
三、例题讲解
四、课堂练习
五、拓展提高
六、课堂总结
七、作业布置
