六年级数学下册试题 一课一练《数与代数-规律探究 》-苏教版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练《数与代数-规律探究 》-苏教版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 552.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-22 19:33:33 | ||
图片预览




文档简介
《数与代数-规律探究
》
一、选一选
1.、,,根据这组有序数对的排列规律,可确定第10个数对是
A.
B.
C.
D.
2.桌上有1张纸,第一次把它剪成3块放回桌上;第二次从桌上拿起1块剪成3块后放回桌上;.进行了这样的8次操作后,桌上一共有 块纸.
A.24
B.21
C.19
D.17
3.观察下列图形的排列规律,第100个图形是
A.
B.
C.
D.无法确定
4.如图所示,按三个图的顺序,第四个图应该是的
A.
B.
C.
D.
5.观察下面的点阵图形,根据圆点的变化,探究其规律,则第8个图形中圆点的个数为
A.25
B.26
C.27
D.29
6.如图,〇、△、□各表示一个两位数中的其中一个数字,观察下面图与数的关系,第4图形表示的两位数是
A.54
B.43
C.34
D.以上都不对
二、填空题(共11小题,每空1分,共22分)
1.找规律,在横线里填适当的数.
(1),,, ,;
(2),,, ,.
2.有一列图形:〇〇★□◆〇〇★□◆〇〇★□◆,根据规律,第71个图形是 .
3.,,.不用计算,直接写出
.
4.,,,,按照这个规律算一算, ; .
5.,小数点后面第2019位上的数是 ,将这个小数“四舍五人”精确到百分位约是 .
6.下列图中有大小不同的平行四边形,第1幅图中有1个,第2幅图中有3个,第3幅图中有5个第5幅图中有 个,第幅图中有 个.
7.根据图1的变化规律,画出图2变化后的形状.
8.如图,不同的图形代表不同的数,方格外的数分别表示所在的这一行或这一列中全体图形所代表的数之和,比如第二行中“〇◇”,根据图示所表示的关系,可以推算出? .
9.小朋友们用小木棒摆图形,如图:
摆1个用6根,摆2个用11根,摆3个用16根摆10个用
根,摆
个用小棒101根.
10.发现规律,完成问题:
根据你发现的规律,第四个正方形里填写 ;请你用关于、、的式子表示 .
11.如图,下面每个图中有多少个白色小正方形和多少个灰色小正方形?
(1)把下面的表格补充完整.
第1个图
第2个图
第3个图
第4个图
白色
1
2
灰色
8
10
(2)照这样接着画下去,第6个图中有 个自色小正方形和 个灰色小正方形.
(3)想一想:照这样的规律,第个图中有 个白色小正方形和 个灰色小正方形.
(4)照这样的规律,如果某个图中灰色小正方形有30个,那么自色小正方形有 个,它是第 个图.
三、判一判
1.在数列“,,,,,,”中,第10个数是
(
)
2.沿道路的一边,按3面红旗、2面黄旗、1面蓝旗的顺序插了一行彩旗.第190面应该是红旗。(
)
3.根据,,,可知(
)
4.教室里按2红1黄1蓝的顺序挂彩灯,共挂了37盏.其中,红灯有19盏,黄灯有9盏,蓝灯也有9盏。(
)
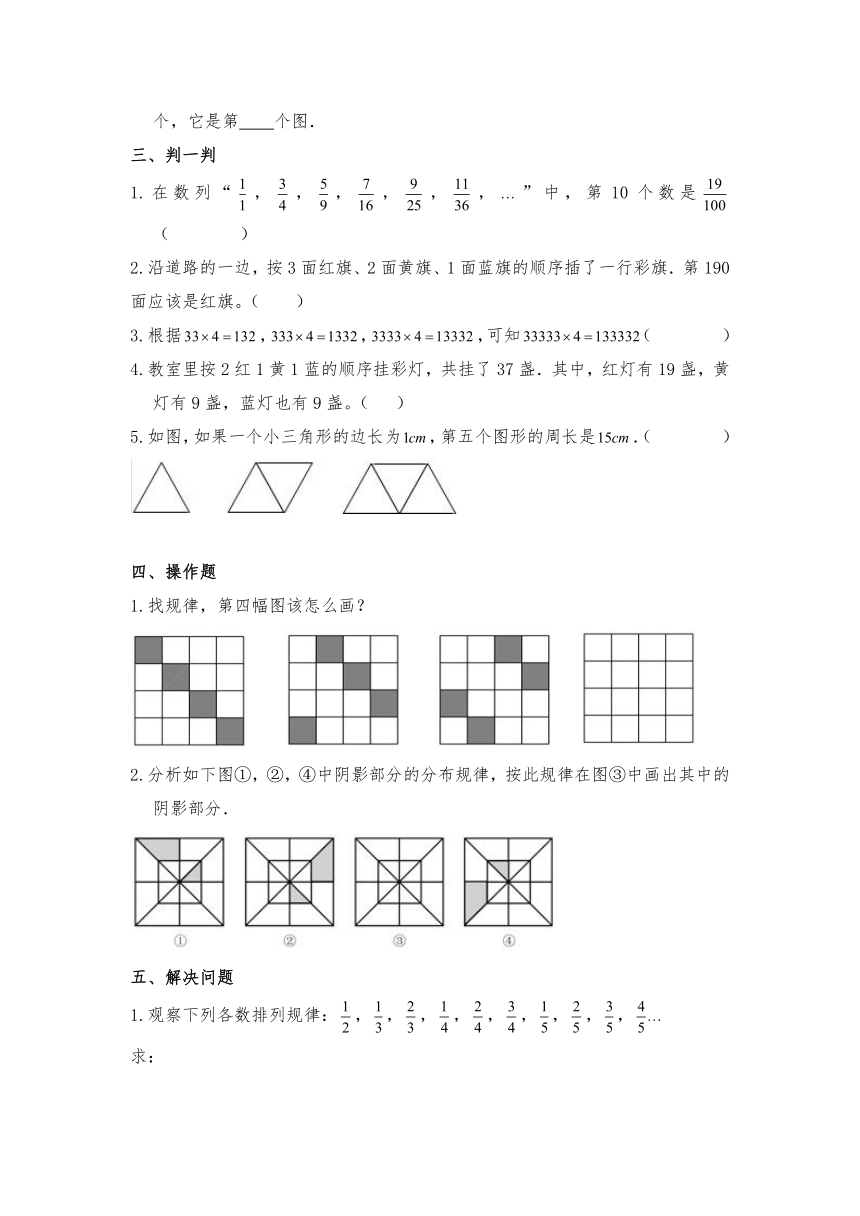
5.如图,如果一个小三角形的边长为,第五个图形的周长是.(
)
四、操作题
1.找规律,第四幅图该怎么画?
2.分析如下图①,②,④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分.
五、解决问题
1.观察下列各数排列规律:,,,,,,,,,
求:
(1)排在第几个位置?
(2)第100个位置上是哪个数?
2.有一些图形按的顺序排列.
(1)请你算一算第50个图形是什么图形?
(2)前35个图形中,占总数的几分之几?
3.观察下表.
一个数
一个数的倒数
一个数与它倒数的和
3
8
9
11
(1)把统计表补充完整
(2)你有什么发现?把你的发现写下来.
(3)如果一个自然数和它的倒数的和是,那么,这个数是多少?
4.找规律.
①在边长为5的方格中涂阴影.(左上角第1块必须涂黑)
②当边长为单数3、5、7、时,黑块与白块的块数有什么规律?
③当边长为双数2、4、6、时,黑块与白块的块数有什么规律?
5.将自然数排列如下,
在这个数阵里,小明用正方形框出九个数.
(1)任意移动几次,每次框住的9个数和与中间的数有什么关系?
(2)如果框住的9个数的和是225,你能列方程,求出中间的一个数吗?
6.探索与发现
意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1、1、2、3、5、8、计算这样的算式时有简便方法吗?
丁丁遇到这个问题时,想到用“数形结合”的方法来探索,于是他以这组数中各个数作为正方形的边长构造成正方形,再拼成如图所示的长方形来研究.
图形
算式
序号
①
②
③
④
(1)观察上面的图形和算式,你能把下面算式补充完整吗?
(2)若按此规律继续拼长方形,则序号为 的长方形面积数是714.
答案
一、选一选
1..2..3..4..5..6..
二、填空题
1.,.
2.〇.
3.9999800001.
4.62;30.
5.8,0.29.
6.9;.
7..
8.9.
9.51,20.
10.97,.
11.(1)3,4,12,14;(2)6,18:;(3),;(4)12,12.
三、判一判
1..2..3..4..5..
四、操作题
1.解:根据分析画图如下:
2.解:画图如下:
五、解决问题
1.解:(1)
答:排在第336个位置.
(2)分母为14的真分数有13个,,第100个的分母为15,第92个为,第93个为,第100个数是.
答:第100个位置上是.
2.解:(1),
答:第50个图形是第9个周期的第2个图形,与第一个周期的第2个图形相同,是□.
(2),
所以前35个图形中占总数的:;
答:前35个图形中,占总数的.
3.解:(1)把统计表补充完整为:
一个数
一个数的倒数
一个数与它倒数的和
3
8
9
11
(2)发现:(一个数与它倒数的和的分子分母这个数.
(3)
答:这个数是6.
4.解:①边长为5的方格中涂阴影,如图:
②边数为3时,黑块有:(块,白块有(块;
边数为5时,黑块有:(块,白块为(块;
边数为7时,黑块有:(块,白块有:(块;
边长是时,黑块块,白块有:块.
答:边长是时,黑块块,白块有:块.
③边数为2时,黑块有(块,白块(块;
边数为4时,黑块(块,白块(块;
边长为时,黑块有:,白块有:块.
答:边长为时,黑块有:,白块有:块.
5.解:(1)
如果框出的9个数是1、2、3,9、10、11,17、18、19
答:每次框住的9个数和是中间的数的9倍.
(2)设中间的一个数为.根据(1)找出的规律
答:中间的一个数是25.
6.解:(1)观察图形和算式,可以发现长方形的长等于数列末项和前一项的和,长方形的宽等于数列的末项,那么求这个数列中数的平方的和就相当于求长方形的面积,长方形面积(末项前一项)末项.
;
(2)根据观察可以发现,第一个图形,是2项的数的平方和,第2个图形,是3项的数的平方和,因为,34是数列1、1、2、3、5、8、13、21、的第9项,所以是第8个图形.
故答案为:(1)3,5;5,8
(2)8
》
一、选一选
1.、,,根据这组有序数对的排列规律,可确定第10个数对是
A.
B.
C.
D.
2.桌上有1张纸,第一次把它剪成3块放回桌上;第二次从桌上拿起1块剪成3块后放回桌上;.进行了这样的8次操作后,桌上一共有 块纸.
A.24
B.21
C.19
D.17
3.观察下列图形的排列规律,第100个图形是
A.
B.
C.
D.无法确定
4.如图所示,按三个图的顺序,第四个图应该是的
A.
B.
C.
D.
5.观察下面的点阵图形,根据圆点的变化,探究其规律,则第8个图形中圆点的个数为
A.25
B.26
C.27
D.29
6.如图,〇、△、□各表示一个两位数中的其中一个数字,观察下面图与数的关系,第4图形表示的两位数是
A.54
B.43
C.34
D.以上都不对
二、填空题(共11小题,每空1分,共22分)
1.找规律,在横线里填适当的数.
(1),,, ,;
(2),,, ,.
2.有一列图形:〇〇★□◆〇〇★□◆〇〇★□◆,根据规律,第71个图形是 .
3.,,.不用计算,直接写出
.
4.,,,,按照这个规律算一算, ; .
5.,小数点后面第2019位上的数是 ,将这个小数“四舍五人”精确到百分位约是 .
6.下列图中有大小不同的平行四边形,第1幅图中有1个,第2幅图中有3个,第3幅图中有5个第5幅图中有 个,第幅图中有 个.
7.根据图1的变化规律,画出图2变化后的形状.
8.如图,不同的图形代表不同的数,方格外的数分别表示所在的这一行或这一列中全体图形所代表的数之和,比如第二行中“〇◇”,根据图示所表示的关系,可以推算出? .
9.小朋友们用小木棒摆图形,如图:
摆1个用6根,摆2个用11根,摆3个用16根摆10个用
根,摆
个用小棒101根.
10.发现规律,完成问题:
根据你发现的规律,第四个正方形里填写 ;请你用关于、、的式子表示 .
11.如图,下面每个图中有多少个白色小正方形和多少个灰色小正方形?
(1)把下面的表格补充完整.
第1个图
第2个图
第3个图
第4个图
白色
1
2
灰色
8
10
(2)照这样接着画下去,第6个图中有 个自色小正方形和 个灰色小正方形.
(3)想一想:照这样的规律,第个图中有 个白色小正方形和 个灰色小正方形.
(4)照这样的规律,如果某个图中灰色小正方形有30个,那么自色小正方形有 个,它是第 个图.
三、判一判
1.在数列“,,,,,,”中,第10个数是
(
)
2.沿道路的一边,按3面红旗、2面黄旗、1面蓝旗的顺序插了一行彩旗.第190面应该是红旗。(
)
3.根据,,,可知(
)
4.教室里按2红1黄1蓝的顺序挂彩灯,共挂了37盏.其中,红灯有19盏,黄灯有9盏,蓝灯也有9盏。(
)
5.如图,如果一个小三角形的边长为,第五个图形的周长是.(
)
四、操作题
1.找规律,第四幅图该怎么画?
2.分析如下图①,②,④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分.
五、解决问题
1.观察下列各数排列规律:,,,,,,,,,
求:
(1)排在第几个位置?
(2)第100个位置上是哪个数?
2.有一些图形按的顺序排列.
(1)请你算一算第50个图形是什么图形?
(2)前35个图形中,占总数的几分之几?
3.观察下表.
一个数
一个数的倒数
一个数与它倒数的和
3
8
9
11
(1)把统计表补充完整
(2)你有什么发现?把你的发现写下来.
(3)如果一个自然数和它的倒数的和是,那么,这个数是多少?
4.找规律.
①在边长为5的方格中涂阴影.(左上角第1块必须涂黑)
②当边长为单数3、5、7、时,黑块与白块的块数有什么规律?
③当边长为双数2、4、6、时,黑块与白块的块数有什么规律?
5.将自然数排列如下,
在这个数阵里,小明用正方形框出九个数.
(1)任意移动几次,每次框住的9个数和与中间的数有什么关系?
(2)如果框住的9个数的和是225,你能列方程,求出中间的一个数吗?
6.探索与发现
意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1、1、2、3、5、8、计算这样的算式时有简便方法吗?
丁丁遇到这个问题时,想到用“数形结合”的方法来探索,于是他以这组数中各个数作为正方形的边长构造成正方形,再拼成如图所示的长方形来研究.
图形
算式
序号
①
②
③
④
(1)观察上面的图形和算式,你能把下面算式补充完整吗?
(2)若按此规律继续拼长方形,则序号为 的长方形面积数是714.
答案
一、选一选
1..2..3..4..5..6..
二、填空题
1.,.
2.〇.
3.9999800001.
4.62;30.
5.8,0.29.
6.9;.
7..
8.9.
9.51,20.
10.97,.
11.(1)3,4,12,14;(2)6,18:;(3),;(4)12,12.
三、判一判
1..2..3..4..5..
四、操作题
1.解:根据分析画图如下:
2.解:画图如下:
五、解决问题
1.解:(1)
答:排在第336个位置.
(2)分母为14的真分数有13个,,第100个的分母为15,第92个为,第93个为,第100个数是.
答:第100个位置上是.
2.解:(1),
答:第50个图形是第9个周期的第2个图形,与第一个周期的第2个图形相同,是□.
(2),
所以前35个图形中占总数的:;
答:前35个图形中,占总数的.
3.解:(1)把统计表补充完整为:
一个数
一个数的倒数
一个数与它倒数的和
3
8
9
11
(2)发现:(一个数与它倒数的和的分子分母这个数.
(3)
答:这个数是6.
4.解:①边长为5的方格中涂阴影,如图:
②边数为3时,黑块有:(块,白块有(块;
边数为5时,黑块有:(块,白块为(块;
边数为7时,黑块有:(块,白块有:(块;
边长是时,黑块块,白块有:块.
答:边长是时,黑块块,白块有:块.
③边数为2时,黑块有(块,白块(块;
边数为4时,黑块(块,白块(块;
边长为时,黑块有:,白块有:块.
答:边长为时,黑块有:,白块有:块.
5.解:(1)
如果框出的9个数是1、2、3,9、10、11,17、18、19
答:每次框住的9个数和是中间的数的9倍.
(2)设中间的一个数为.根据(1)找出的规律
答:中间的一个数是25.
6.解:(1)观察图形和算式,可以发现长方形的长等于数列末项和前一项的和,长方形的宽等于数列的末项,那么求这个数列中数的平方的和就相当于求长方形的面积,长方形面积(末项前一项)末项.
;
(2)根据观察可以发现,第一个图形,是2项的数的平方和,第2个图形,是3项的数的平方和,因为,34是数列1、1、2、3、5、8、13、21、的第9项,所以是第8个图形.
故答案为:(1)3,5;5,8
(2)8
