2020-2021学年七年级数学冀教版下册《第7章相交线与平行线》期中复习能力提升训练(word版含解析)
文档属性
| 名称 | 2020-2021学年七年级数学冀教版下册《第7章相交线与平行线》期中复习能力提升训练(word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 208.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-22 21:07:59 | ||
图片预览

文档简介
2021年冀教版七年级数学下册《第7章相交线与平行线》期中复习能力提升训练(附答案)
1.如图,若AD∥BC,则下列结论正确的是( )
A.∠1=∠3
B.∠2=∠4
C.∠1=∠2
D.∠2=∠3
2.如图,在下列条件中,不能判定直线a与b平行的是( )
A.∠1=∠2
B.∠2=∠3
C.∠1=∠5
D.∠3+∠4=180°
3.如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )
A.β=α+γ
B.α+β﹣γ=90°
C.α+β+γ=180°
D.β+γ﹣α=90°
4.如图,要把河中的水引到村庄A,小凡先作AB⊥CD,垂足为点B,然后沿AB开挖水渠,就能使所开挖的水渠最短,其依据是( )
A.两点确定一条直线
B.两点之间线段最短
C.在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线
D.连接直线外一点与直线上各点的所有线段中,垂线段最短
5.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3( )
A.70°
B.180°
C.110°
D.80°
6.如图,直线DE与BC相交于点O,∠1与∠2互余,∠AOE=116°,则∠BOE的度数是( )
A.144°
B.164°
C.154°
D.150°
7.如图所示,l1∥l2,三角板ABC如图放置,其中∠B=90°,若∠1=40°,则∠2的度数是( )
A.40°
B.50°
C.60°
D.30°
8.已知:如图,AB∥EF,∠ABC=75°,∠CDF=135°,则∠BCD=
度.
9.如图,若a∥b,则图中x的度数是
度.
10.如图,∠AOB的一边OA为平面镜,∠AOB=38°,一束光线(与水平线OB平行)从点C射入经平面镜反射后,反射光线落在OB上的点E处,则∠DEB的度数是
度.
11.如图,若AB∥CD,∠C=58°,∠A=18°,则∠E=
°.
12.如图,将△ABC沿BC方向平移至△DEF处.若EC=2BE=2,则CF的长为
.
13.如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为
.
14.如图,两个直角三角形重叠在一起,将其中一个沿点B到点C的方向平移到△DEF的位置,AB=10,BC=15,平移距离为5,则阴影部分的面积为
.
15.如图,如果AB∥CD,那么∠BAE+∠AEC+∠ECD=
°.
16.如图,点E是BA延长线上一点,在下列条件中:①∠1=∠3;②∠5=∠B;③∠1=∠4且AC平分∠DAB;④∠B+∠BCD=180°,能判定AB∥CD的有
.(填序号)
17.如图,已知AE∥CD,BC⊥CD于C,若∠A=28°,则∠ABC=
°.
18.如图,这是购物车的侧面示意图,扶手AB与车底CD平行,∠1=100°,∠2=50°,则∠3的度数是
.
19.如图,如果AB∥CD,则角α=130°,γ=20°,则β=
.
20.如图,∠ABC和∠BCD的平分线交于点P,延长CP交AB于点Q,且∠PBC+∠PCB=90°.
(1)求证:AB∥CD.
(2)探究∠PBC与∠PQB的数量关系.
21.如图,AB∥CD.
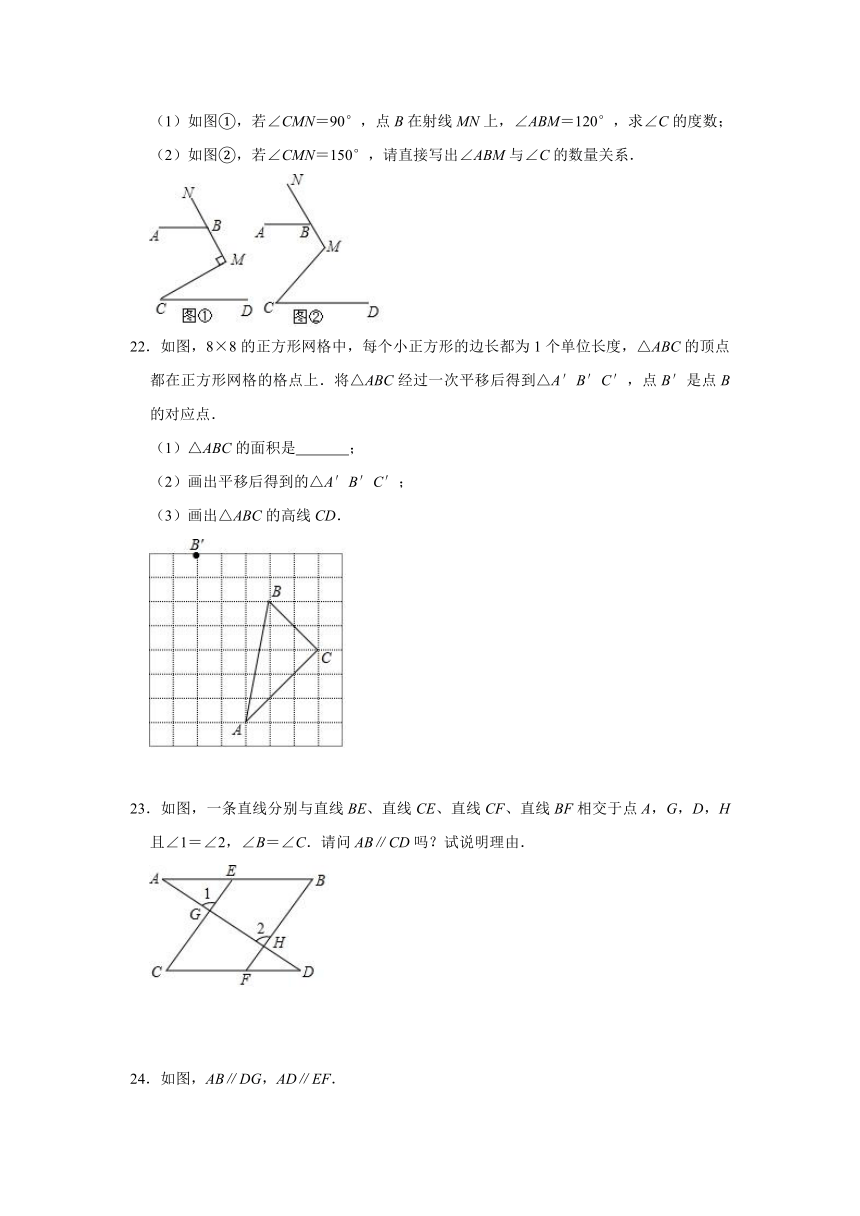
(1)如图①,若∠CMN=90°,点B在射线MN上,∠ABM=120°,求∠C的度数;
(2)如图②,若∠CMN=150°,请直接写出∠ABM与∠C的数量关系.
22.如图,8×8的正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的顶点都在正方形网格的格点上.将△ABC经过一次平移后得到△A′B′C′,点B′是点B的对应点.
(1)△ABC的面积是
;
(2)画出平移后得到的△A′B′C′;
(3)画出△ABC的高线CD.
23.如图,一条直线分别与直线BE、直线CE、直线CF、直线BF相交于点A,G,D,H且∠1=∠2,∠B=∠C.请问AB∥CD吗?试说明理由.
24.如图,AB∥DG,AD∥EF.
(1)试说明:∠1+∠2=180°;
(2)若DG是∠ADC的平分线,∠2=138°,求∠B的度数.
25.如图,CD∥EF,AC⊥AE,且∠α和∠β的度数满足方程组
(1)求∠α和∠β的度数.
(2)求证:AB∥CD.
(3)求∠C的度数.
26.如图,DB∥FG∥EC,A是FG上的一点,∠ADB=60°,∠ACE=36°,AP平分∠CAD,求∠PAG的度数.
27.如图,直线EF分别交直线AB,CD于E,F两点,过点E作EG⊥EF交直线CD于点G,点H是直线AB上一点,连接FH,已知∠1+∠2=90°.
(1)求证:AB∥CD;
(2)若∠2=40°,FH平分∠CFE,求∠CFH的度数.
参考答案
1.解:∵AD∥BC,
∴∠3=∠1,
故选:A.
2.解:A、∵∠1=∠2,∴a∥b,不符合题意;
B、∵∠2=∠3,∴a∥b,不符合题意;
C、∵∠1与∠5既不是直线a,b被任何一条直线所截的一组同位角,内错角,
∴∠1=∠5,不能得到a∥b,
∴符合题意;
D、∵∠3+∠4=180°,∴a∥b,不符合题意;
故选:C.
3.解:延长DC交AB与G,延长CD交EF于H.
直角△BGC中,∠1=90°﹣α;
△EHD中,∠2=β﹣γ,
∵AB∥EF,
∴∠1=∠2,
∴90°﹣α=β﹣γ,
即α+β﹣γ=90°.
故选:B.
4.解:先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是垂线段最短;
故答案为:垂线段最短.
故选:D.
5.解:延长直线,如图:
,
∵直线a平移后得到直线b,
∴a∥b,
∴∠5=180°﹣∠1=180°﹣70°=110°,
∵∠2=∠4+∠5,
∵∠3=∠4,
∴∠2﹣∠3=∠5=110°,
故选:C.
6.解:∵∠1与∠2互余,
∴∠1+∠2=90°,
∴∠AOC=90°,
∴∠COE=∠AOE﹣∠AOC=26°,
∵直线DE与BC相交于点O,
∴∠BOD=∠COE=26°,
∴∠BOE=180°﹣∠BOD=154°,
故选:C.
7.解:作BD∥l1,如图所示:
∵BD∥l1,∠1=40°,
∴∠1=∠ABD=40°,
又∵l1∥l2,
∴BD∥l2,
∴∠CBD=∠2,
又∵∠CBA=∠CBD+∠ABD=90°,
∴∠CBD=50°,
∴∠2=50°.
故选:B.
8.解:∵∠CDF=135°,
∴∠EDC=180°﹣135°=45°,
∵AB∥EF,∠ABC=75°,
∴∠1=∠ABC=75°,
∴∠BCD=∠1﹣∠EDC=75°﹣45°=30°,
故答案为:30.
9.解:∠1=180°﹣120°=60°,
如图,过两平行线中间角的顶点作a的平行线,
由平行线的性质可得x+48°=60°+30°+30°,
解得x=72°.
故答案为:72.
10.解:∵DC∥OB,
∴∠ADC=∠AOB=38°,
由光线的反射定理易得,∠ODE=∠ADC=38°,
∠DEB=∠ODE+∠AOB=38°+38°=76°,
故答案为:76°.
11.解:如图,
∵AB∥CD,
∴∠C=∠BFE=58°,
∵∠BFE=∠A+∠E,
∴∠E=58°﹣18°=40°.
故答案为40°.
12.解:∵△ABC沿BC方向平移至△DEF处.
∴BE=CF,
∵EC=2BE=2,
∴BE=1,
∴CF=1.
故答案为1.
13.解:∵AB⊥AE,∠CAE=42°,
∴∠BAC=90°﹣42°=48°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠ACD=132°.
故答案为:132°.
14.解:∵△DEF是由△ABC平移得到,
∴S△ABC=S△DEF,
∴S阴=S梯形ABEH,
∵HE∥AB,
∴EH=,
∴S阴=×(10+)×5=
15.解:作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BAE+∠AEF=180°,∠FEC+∠ECD=180°,
∵∠AEF+∠FEC=∠AEC,
∴∠BAE+∠AEC+∠ECD=360°,
故答案为:360.
16.解:①中,∵∠1=∠3,∴AD∥BC(内错角相等,两直线平行),不合题意;
②中,∵∠5=∠B,∴AD∥BC(同位角相等,两直线平行),不合题意;
③中,∵∠1=∠4且AC平分∠DAB,∴∠2=∠4,∴AB∥CD,故此选项符合题意;
④中,∠B+∠BCD=180°,∴AB∥CD
(同旁内角互补,两直线平行),故此选项符合题意;
故答案为:③④.
17.解:如图,过B作BM∥AE,
∴∠A=∠ABM,∠MBC=∠C,
∵∠A=28°,
∴∠ABM=28°,
∵BC⊥CD于C,
∴∠C=90°,
∴∠MBC=90°,
∴∠ABC=∠ABM+∠MBC=28°+90°=118°,
故答案为118°.
18.解:∵AB∥CD,
∴∠1=∠CDA=100°,
∵∠2=50°,
∴∠3=50°.
故答案为:50°.
19.解:如图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A+∠AEF=180°,∠D=∠FED,
∴∠AEF=180°﹣130°=50°,∠FED=20°,
∴∠AED=∠AEF+∠FED=50°+20°=70°.
即β=70°.
故答案为:70°.
20.(1)证明:∵BP平分∠ABC,
∴∠ABC=2∠PBC.
∵CP平分∠BCD,
∴∠BCD=2∠PCB,
∴∠ABC+∠BCD=2∠PBC+2∠PCB,
又∵∠PBC+∠PCB=90°,
∴∠ABC+∠BCD=180°,
∴AB∥CD.
(2)∵CP平分∠DCB,
∴∠PCD=∠PCB.
∵AB∥CD,
∴∠PCD=∠PQB,
∴∠PCB=∠PQB.
又∵∠PBC+∠PCB=90°,
∴∠PBC+∠PQB=90°.
21.解:(1)如图①,过M作MK∥AB,则∠ABM+∠1=180°,
∴∠1=180°﹣∠ABM=60°,
∵∠CMN=90°,
∴∠2=90°﹣∠1=30°,
∵AB∥CD,MK∥AB,
∴MK∥CD,
∴∠C=∠2=30°;
(2)∠ABM﹣∠C=30°,
理由:如图②,过M作MK∥AB,则∠ABM+∠1=180°,
∴∠1=180°﹣∠ABM,
∵AB∥CD,MK∥AB,
∴MK∥CD,
∴∠C=∠2,
∵∠CMN=∠1+∠2=150°,即180°﹣∠ABM+∠C=150°,
∴∠ABM﹣∠C=180°﹣150°=30°.
22.解:(1)△ABC的面积=3×5﹣×2×2﹣×3×3﹣×5×1=6;
故答案为6;
(2)如图,△A′B′C′为所作;
(3)如图,CD为所作.
23.解:AB∥CD.
理由如下:∵∠1=∠2(已知),
∴CE∥FB(同位角相等,两直线平行),
∵CE∥FB,
∴∠C=∠BFD(两直线平行,同位角相等),
∵∠B=∠C(已知),
∴∠B=∠BFD(等量代换),
∴AB∥CD(内错角相等,两直线平行).
24.解:(1)∵AD∥EF,
∴∠BAD+∠2=180°,
∵AB∥DG,
∴∠BAD=∠1,
∴∠1+∠2=180°.
(2)∵∠1+∠2=180°且∠2=138°,
∴∠1=42°,
∵DG是∠ADC的平分线,
∴∠CDG=∠1=42°,
∵AB∥DG,
∴∠B=∠CDG=42°.
25.解:(1),
①﹣②,得
3∠α=165°,
解得,∠α=55°,
把∠α=55°代入②,得
∠β=125°,
即∠α和∠β的度数分别为55°,125°;
(2)证明:由(1)知,∠α=55°,∠β=125°,
则∠α+∠β=180°,
故AB∥EF,
又∵CD∥EF,
∴AB∥CD;
(3)∵AB∥CD,
∴∠BAC+∠C=180°,
∵AC⊥AE,
∴∠CAE=90°,
又∵∠α=55°,
∴∠BAC=145°,
∴∠C=35°.
26.解:∵DB∥FG∥EC,
∴∠BDA=∠DAG,∠ACE=∠CAG,
∵∠ADB=60°,∠ACE=36°,
∴∠DAG=60°,∠CAG=36°,
∴∠DAC=96°,
∵AP平分∠CAD,
∴∠CAP=48°,
∴∠PAG=12°.
27.证明:(1)∵EG⊥EF,
∴∠FEG=90°,
∵∠1+∠2=90°,
∴∠AEG+∠EGF=∠+∠2+∠FEG=90°+90°=180°,
∴AB∥CD;
(2)∵AB∥CD,∠2=40°,
∴∠1=50°,
∴∠EFG=∠1=50°,
∴∠CFE=130°,
∵FH平分∠CFE,
∴∠CFH=65°.
1.如图,若AD∥BC,则下列结论正确的是( )
A.∠1=∠3
B.∠2=∠4
C.∠1=∠2
D.∠2=∠3
2.如图,在下列条件中,不能判定直线a与b平行的是( )
A.∠1=∠2
B.∠2=∠3
C.∠1=∠5
D.∠3+∠4=180°
3.如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )
A.β=α+γ
B.α+β﹣γ=90°
C.α+β+γ=180°
D.β+γ﹣α=90°
4.如图,要把河中的水引到村庄A,小凡先作AB⊥CD,垂足为点B,然后沿AB开挖水渠,就能使所开挖的水渠最短,其依据是( )
A.两点确定一条直线
B.两点之间线段最短
C.在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线
D.连接直线外一点与直线上各点的所有线段中,垂线段最短
5.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3( )
A.70°
B.180°
C.110°
D.80°
6.如图,直线DE与BC相交于点O,∠1与∠2互余,∠AOE=116°,则∠BOE的度数是( )
A.144°
B.164°
C.154°
D.150°
7.如图所示,l1∥l2,三角板ABC如图放置,其中∠B=90°,若∠1=40°,则∠2的度数是( )
A.40°
B.50°
C.60°
D.30°
8.已知:如图,AB∥EF,∠ABC=75°,∠CDF=135°,则∠BCD=
度.
9.如图,若a∥b,则图中x的度数是
度.
10.如图,∠AOB的一边OA为平面镜,∠AOB=38°,一束光线(与水平线OB平行)从点C射入经平面镜反射后,反射光线落在OB上的点E处,则∠DEB的度数是
度.
11.如图,若AB∥CD,∠C=58°,∠A=18°,则∠E=
°.
12.如图,将△ABC沿BC方向平移至△DEF处.若EC=2BE=2,则CF的长为
.
13.如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为
.
14.如图,两个直角三角形重叠在一起,将其中一个沿点B到点C的方向平移到△DEF的位置,AB=10,BC=15,平移距离为5,则阴影部分的面积为
.
15.如图,如果AB∥CD,那么∠BAE+∠AEC+∠ECD=
°.
16.如图,点E是BA延长线上一点,在下列条件中:①∠1=∠3;②∠5=∠B;③∠1=∠4且AC平分∠DAB;④∠B+∠BCD=180°,能判定AB∥CD的有
.(填序号)
17.如图,已知AE∥CD,BC⊥CD于C,若∠A=28°,则∠ABC=
°.
18.如图,这是购物车的侧面示意图,扶手AB与车底CD平行,∠1=100°,∠2=50°,则∠3的度数是
.
19.如图,如果AB∥CD,则角α=130°,γ=20°,则β=
.
20.如图,∠ABC和∠BCD的平分线交于点P,延长CP交AB于点Q,且∠PBC+∠PCB=90°.
(1)求证:AB∥CD.
(2)探究∠PBC与∠PQB的数量关系.
21.如图,AB∥CD.
(1)如图①,若∠CMN=90°,点B在射线MN上,∠ABM=120°,求∠C的度数;
(2)如图②,若∠CMN=150°,请直接写出∠ABM与∠C的数量关系.
22.如图,8×8的正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的顶点都在正方形网格的格点上.将△ABC经过一次平移后得到△A′B′C′,点B′是点B的对应点.
(1)△ABC的面积是
;
(2)画出平移后得到的△A′B′C′;
(3)画出△ABC的高线CD.
23.如图,一条直线分别与直线BE、直线CE、直线CF、直线BF相交于点A,G,D,H且∠1=∠2,∠B=∠C.请问AB∥CD吗?试说明理由.
24.如图,AB∥DG,AD∥EF.
(1)试说明:∠1+∠2=180°;
(2)若DG是∠ADC的平分线,∠2=138°,求∠B的度数.
25.如图,CD∥EF,AC⊥AE,且∠α和∠β的度数满足方程组
(1)求∠α和∠β的度数.
(2)求证:AB∥CD.
(3)求∠C的度数.
26.如图,DB∥FG∥EC,A是FG上的一点,∠ADB=60°,∠ACE=36°,AP平分∠CAD,求∠PAG的度数.
27.如图,直线EF分别交直线AB,CD于E,F两点,过点E作EG⊥EF交直线CD于点G,点H是直线AB上一点,连接FH,已知∠1+∠2=90°.
(1)求证:AB∥CD;
(2)若∠2=40°,FH平分∠CFE,求∠CFH的度数.
参考答案
1.解:∵AD∥BC,
∴∠3=∠1,
故选:A.
2.解:A、∵∠1=∠2,∴a∥b,不符合题意;
B、∵∠2=∠3,∴a∥b,不符合题意;
C、∵∠1与∠5既不是直线a,b被任何一条直线所截的一组同位角,内错角,
∴∠1=∠5,不能得到a∥b,
∴符合题意;
D、∵∠3+∠4=180°,∴a∥b,不符合题意;
故选:C.
3.解:延长DC交AB与G,延长CD交EF于H.
直角△BGC中,∠1=90°﹣α;
△EHD中,∠2=β﹣γ,
∵AB∥EF,
∴∠1=∠2,
∴90°﹣α=β﹣γ,
即α+β﹣γ=90°.
故选:B.
4.解:先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是垂线段最短;
故答案为:垂线段最短.
故选:D.
5.解:延长直线,如图:
,
∵直线a平移后得到直线b,
∴a∥b,
∴∠5=180°﹣∠1=180°﹣70°=110°,
∵∠2=∠4+∠5,
∵∠3=∠4,
∴∠2﹣∠3=∠5=110°,
故选:C.
6.解:∵∠1与∠2互余,
∴∠1+∠2=90°,
∴∠AOC=90°,
∴∠COE=∠AOE﹣∠AOC=26°,
∵直线DE与BC相交于点O,
∴∠BOD=∠COE=26°,
∴∠BOE=180°﹣∠BOD=154°,
故选:C.
7.解:作BD∥l1,如图所示:
∵BD∥l1,∠1=40°,
∴∠1=∠ABD=40°,
又∵l1∥l2,
∴BD∥l2,
∴∠CBD=∠2,
又∵∠CBA=∠CBD+∠ABD=90°,
∴∠CBD=50°,
∴∠2=50°.
故选:B.
8.解:∵∠CDF=135°,
∴∠EDC=180°﹣135°=45°,
∵AB∥EF,∠ABC=75°,
∴∠1=∠ABC=75°,
∴∠BCD=∠1﹣∠EDC=75°﹣45°=30°,
故答案为:30.
9.解:∠1=180°﹣120°=60°,
如图,过两平行线中间角的顶点作a的平行线,
由平行线的性质可得x+48°=60°+30°+30°,
解得x=72°.
故答案为:72.
10.解:∵DC∥OB,
∴∠ADC=∠AOB=38°,
由光线的反射定理易得,∠ODE=∠ADC=38°,
∠DEB=∠ODE+∠AOB=38°+38°=76°,
故答案为:76°.
11.解:如图,
∵AB∥CD,
∴∠C=∠BFE=58°,
∵∠BFE=∠A+∠E,
∴∠E=58°﹣18°=40°.
故答案为40°.
12.解:∵△ABC沿BC方向平移至△DEF处.
∴BE=CF,
∵EC=2BE=2,
∴BE=1,
∴CF=1.
故答案为1.
13.解:∵AB⊥AE,∠CAE=42°,
∴∠BAC=90°﹣42°=48°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠ACD=132°.
故答案为:132°.
14.解:∵△DEF是由△ABC平移得到,
∴S△ABC=S△DEF,
∴S阴=S梯形ABEH,
∵HE∥AB,
∴EH=,
∴S阴=×(10+)×5=
15.解:作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BAE+∠AEF=180°,∠FEC+∠ECD=180°,
∵∠AEF+∠FEC=∠AEC,
∴∠BAE+∠AEC+∠ECD=360°,
故答案为:360.
16.解:①中,∵∠1=∠3,∴AD∥BC(内错角相等,两直线平行),不合题意;
②中,∵∠5=∠B,∴AD∥BC(同位角相等,两直线平行),不合题意;
③中,∵∠1=∠4且AC平分∠DAB,∴∠2=∠4,∴AB∥CD,故此选项符合题意;
④中,∠B+∠BCD=180°,∴AB∥CD
(同旁内角互补,两直线平行),故此选项符合题意;
故答案为:③④.
17.解:如图,过B作BM∥AE,
∴∠A=∠ABM,∠MBC=∠C,
∵∠A=28°,
∴∠ABM=28°,
∵BC⊥CD于C,
∴∠C=90°,
∴∠MBC=90°,
∴∠ABC=∠ABM+∠MBC=28°+90°=118°,
故答案为118°.
18.解:∵AB∥CD,
∴∠1=∠CDA=100°,
∵∠2=50°,
∴∠3=50°.
故答案为:50°.
19.解:如图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A+∠AEF=180°,∠D=∠FED,
∴∠AEF=180°﹣130°=50°,∠FED=20°,
∴∠AED=∠AEF+∠FED=50°+20°=70°.
即β=70°.
故答案为:70°.
20.(1)证明:∵BP平分∠ABC,
∴∠ABC=2∠PBC.
∵CP平分∠BCD,
∴∠BCD=2∠PCB,
∴∠ABC+∠BCD=2∠PBC+2∠PCB,
又∵∠PBC+∠PCB=90°,
∴∠ABC+∠BCD=180°,
∴AB∥CD.
(2)∵CP平分∠DCB,
∴∠PCD=∠PCB.
∵AB∥CD,
∴∠PCD=∠PQB,
∴∠PCB=∠PQB.
又∵∠PBC+∠PCB=90°,
∴∠PBC+∠PQB=90°.
21.解:(1)如图①,过M作MK∥AB,则∠ABM+∠1=180°,
∴∠1=180°﹣∠ABM=60°,
∵∠CMN=90°,
∴∠2=90°﹣∠1=30°,
∵AB∥CD,MK∥AB,
∴MK∥CD,
∴∠C=∠2=30°;
(2)∠ABM﹣∠C=30°,
理由:如图②,过M作MK∥AB,则∠ABM+∠1=180°,
∴∠1=180°﹣∠ABM,
∵AB∥CD,MK∥AB,
∴MK∥CD,
∴∠C=∠2,
∵∠CMN=∠1+∠2=150°,即180°﹣∠ABM+∠C=150°,
∴∠ABM﹣∠C=180°﹣150°=30°.
22.解:(1)△ABC的面积=3×5﹣×2×2﹣×3×3﹣×5×1=6;
故答案为6;
(2)如图,△A′B′C′为所作;
(3)如图,CD为所作.
23.解:AB∥CD.
理由如下:∵∠1=∠2(已知),
∴CE∥FB(同位角相等,两直线平行),
∵CE∥FB,
∴∠C=∠BFD(两直线平行,同位角相等),
∵∠B=∠C(已知),
∴∠B=∠BFD(等量代换),
∴AB∥CD(内错角相等,两直线平行).
24.解:(1)∵AD∥EF,
∴∠BAD+∠2=180°,
∵AB∥DG,
∴∠BAD=∠1,
∴∠1+∠2=180°.
(2)∵∠1+∠2=180°且∠2=138°,
∴∠1=42°,
∵DG是∠ADC的平分线,
∴∠CDG=∠1=42°,
∵AB∥DG,
∴∠B=∠CDG=42°.
25.解:(1),
①﹣②,得
3∠α=165°,
解得,∠α=55°,
把∠α=55°代入②,得
∠β=125°,
即∠α和∠β的度数分别为55°,125°;
(2)证明:由(1)知,∠α=55°,∠β=125°,
则∠α+∠β=180°,
故AB∥EF,
又∵CD∥EF,
∴AB∥CD;
(3)∵AB∥CD,
∴∠BAC+∠C=180°,
∵AC⊥AE,
∴∠CAE=90°,
又∵∠α=55°,
∴∠BAC=145°,
∴∠C=35°.
26.解:∵DB∥FG∥EC,
∴∠BDA=∠DAG,∠ACE=∠CAG,
∵∠ADB=60°,∠ACE=36°,
∴∠DAG=60°,∠CAG=36°,
∴∠DAC=96°,
∵AP平分∠CAD,
∴∠CAP=48°,
∴∠PAG=12°.
27.证明:(1)∵EG⊥EF,
∴∠FEG=90°,
∵∠1+∠2=90°,
∴∠AEG+∠EGF=∠+∠2+∠FEG=90°+90°=180°,
∴AB∥CD;
(2)∵AB∥CD,∠2=40°,
∴∠1=50°,
∴∠EFG=∠1=50°,
∴∠CFE=130°,
∵FH平分∠CFE,
∴∠CFH=65°.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
