2.1.1 两条直线的位置关系 同步练习(含答案)
文档属性
| 名称 | 2.1.1 两条直线的位置关系 同步练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-23 07:59:52 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2.1.1 两条直线的位置关系同步练习
一、选择题。
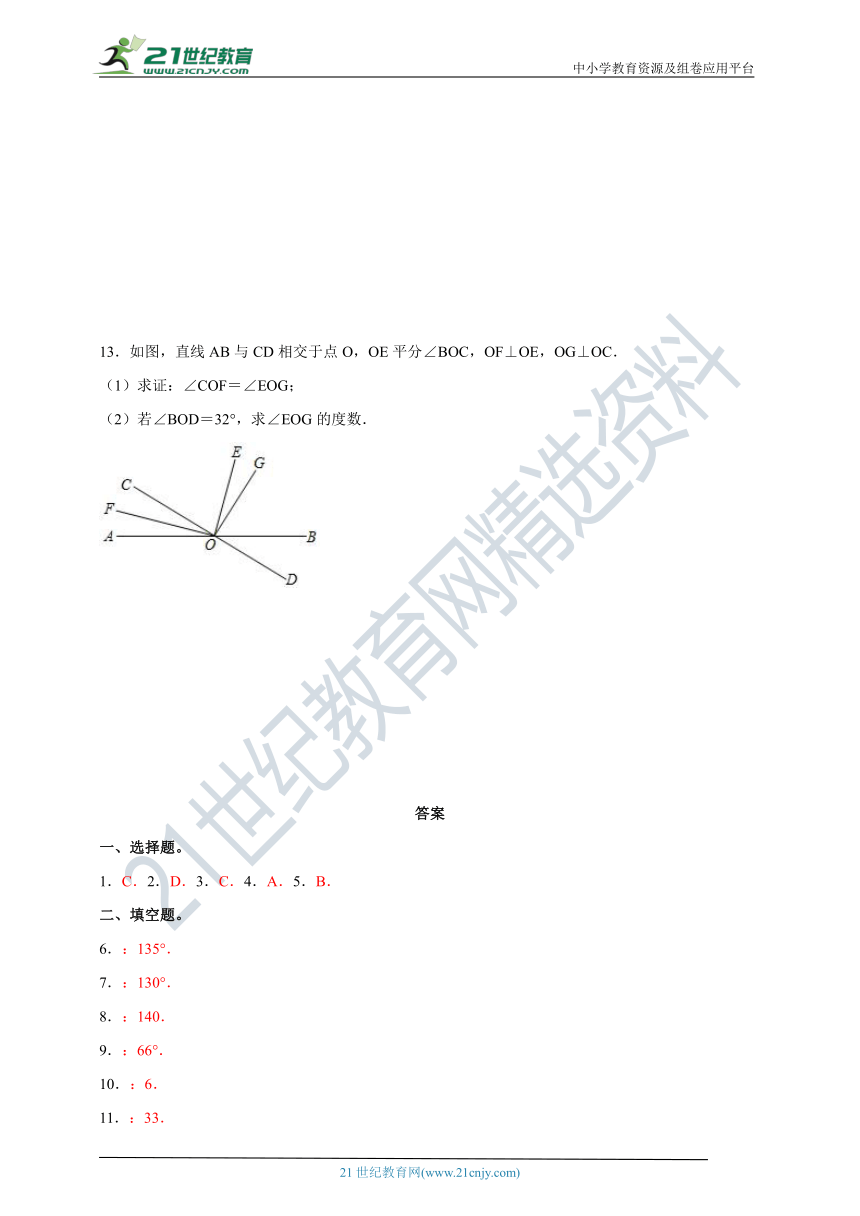
1.下列四个图形中,∠1=∠2一定成立的是( )
A. B.
C. D.
2.如图,将一副三角板按不同位置摆放,其中α和β互为补角的是( )
A. B.
C. D.
3.若∠A=30°,则∠A的余角等于( )
4.如图,要测量两堵围墙形成的∠AOB的度数,但人不能进入围墙,可先延长BO得到∠AOC,然后测量∠AOC的度数,再计算出∠AOB的度数,其中依据的原理是( )
A.同角的补角相等 B.同角的余角相等
C.等角的余角相等 D.两点之间线段最短
5.如图,已知∠1=∠2,∠3=∠4,∠BOD=∠AOB=90°.下列判断:①射线OF是∠BOE的角平分线;②∠DOE的补角是∠BOC;③∠AOC的余角只有∠COD;④∠DOE的余角有∠BOE和∠COD;⑤∠COD=∠BOE.其中正确的有( )
A.5个 B.4个 C.3个 D.2个
二、填空题。
6.若一个角和它的余角相等,则这个角的补角的度数为 .
7.已知∠A与∠B互补,且∠A等于3∠B﹣20°,则∠A= .
8.如图,∠1和∠2互为补角,∠1=40°,则∠2= °.
9.如图,直线AB、CD相交于点O,∠COE是直角,OF平分∠AOD,若∠BOE=42°,则∠AOF的度数是 .
10.如图,点O在直线AB上,∠AOD=120°,CO⊥AB,OE平分∠BOD,则图中一共有 对互补的角.
11.如图所示,O是直线AB与CD的交点,∠BOM:∠DOM=1:2,∠CON=90°,∠NOM=68°,则∠BOD= °.
三、解答题。
12.已知一个角的补角比这个角的余角的2倍大10°,求这个角的度数.
13.如图,直线AB与CD相交于点O,OE平分∠BOC,OF⊥OE,OG⊥OC.
(1)求证:∠COF=∠EOG;
(2)若∠BOD=32°,求∠EOG的度数.
答案
一、选择题。
1.C.2.D.3.C.4.A.5.B.
二、填空题。
6.:135°.
7.:130°.
8.:140.
9.:66°.
10.:6.
11.:33.
三、解答题。
12.【解答】解:设这个角的度数为x,
依题意有:(180°﹣x)﹣2(90°﹣x)=10°,
解得x=10°,
故这个角的度数为10°.
13.【解答】(1)证明:∵OF⊥OE,OG⊥OC,
∴∠FOE=∠COF+∠COE=90°,∠COG=∠EOG+∠COE=90°,
∴∠COF=∠EOG;
(2)解:∵∠BOD=32°,
∴∠BOC=180°﹣32°=148°,
∵OE平分∠BOC,
∴∠COE=∠BOC=74°,
∵∠COG=90°,
∴∠EOG=∠COG﹣∠COE=16°.
_21?????????è?????(www.21cnjy.com)_
2.1.1 两条直线的位置关系同步练习
一、选择题。
1.下列四个图形中,∠1=∠2一定成立的是( )
A. B.
C. D.
2.如图,将一副三角板按不同位置摆放,其中α和β互为补角的是( )
A. B.
C. D.
3.若∠A=30°,则∠A的余角等于( )
4.如图,要测量两堵围墙形成的∠AOB的度数,但人不能进入围墙,可先延长BO得到∠AOC,然后测量∠AOC的度数,再计算出∠AOB的度数,其中依据的原理是( )
A.同角的补角相等 B.同角的余角相等
C.等角的余角相等 D.两点之间线段最短
5.如图,已知∠1=∠2,∠3=∠4,∠BOD=∠AOB=90°.下列判断:①射线OF是∠BOE的角平分线;②∠DOE的补角是∠BOC;③∠AOC的余角只有∠COD;④∠DOE的余角有∠BOE和∠COD;⑤∠COD=∠BOE.其中正确的有( )
A.5个 B.4个 C.3个 D.2个
二、填空题。
6.若一个角和它的余角相等,则这个角的补角的度数为 .
7.已知∠A与∠B互补,且∠A等于3∠B﹣20°,则∠A= .
8.如图,∠1和∠2互为补角,∠1=40°,则∠2= °.
9.如图,直线AB、CD相交于点O,∠COE是直角,OF平分∠AOD,若∠BOE=42°,则∠AOF的度数是 .
10.如图,点O在直线AB上,∠AOD=120°,CO⊥AB,OE平分∠BOD,则图中一共有 对互补的角.
11.如图所示,O是直线AB与CD的交点,∠BOM:∠DOM=1:2,∠CON=90°,∠NOM=68°,则∠BOD= °.
三、解答题。
12.已知一个角的补角比这个角的余角的2倍大10°,求这个角的度数.
13.如图,直线AB与CD相交于点O,OE平分∠BOC,OF⊥OE,OG⊥OC.
(1)求证:∠COF=∠EOG;
(2)若∠BOD=32°,求∠EOG的度数.
答案
一、选择题。
1.C.2.D.3.C.4.A.5.B.
二、填空题。
6.:135°.
7.:130°.
8.:140.
9.:66°.
10.:6.
11.:33.
三、解答题。
12.【解答】解:设这个角的度数为x,
依题意有:(180°﹣x)﹣2(90°﹣x)=10°,
解得x=10°,
故这个角的度数为10°.
13.【解答】(1)证明:∵OF⊥OE,OG⊥OC,
∴∠FOE=∠COF+∠COE=90°,∠COG=∠EOG+∠COE=90°,
∴∠COF=∠EOG;
(2)解:∵∠BOD=32°,
∴∠BOC=180°﹣32°=148°,
∵OE平分∠BOC,
∴∠COE=∠BOC=74°,
∵∠COG=90°,
∴∠EOG=∠COG﹣∠COE=16°.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
