7.1 行星的运动 (强化提高)检测— 2020-2021学年【新教材】人教版(2019)高中物理必修第二册(含解析)
文档属性
| 名称 | 7.1 行星的运动 (强化提高)检测— 2020-2021学年【新教材】人教版(2019)高中物理必修第二册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 403.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-22 00:00:00 | ||
图片预览




文档简介
第七章万有引力与宇宙航行第一节行星的运动强化训练(含解析)
一、单选题
1.位于贵州的“中国天眼”(FAST)是目前世界上口径最大的单天线射电望远镜,通过FAST可以测量地球与木星之间的距离。当FAST接收到来自木星的光线传播方向恰好与地球公转线速度方向相同时,测得地球与木星的距离是地球与太阳距离的k倍。若地球和木星绕太阳的运动均视为匀速圆周运动且轨道共面,则可知木星的公转周期为( )
A.年 B.年 C.年 D.年
2.地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆。天文学家哈雷曾经在1662年跟踪过一颗彗星,他算出这颗彗星轨道的半长轴约等于地球公转半径的18倍,并预言这颗彗星将每隔一定时间就会再次出现。这颗彗星最近出现的时间是1986年,它下次飞近地球大约是哪一年( )
A.2042年 B.2052年 C.2062年 D.2072年
3.设金星和地球绕太阳中心的运动是公转方向相同且轨道共面的匀速圆周运动,金星在地球轨道的内侧(称为地内行星)。在某些特殊时刻,地球、金星和太阳会出现在一条直线上,这时候从地球上观测,金星像镶嵌在太阳脸上的小黑痣缓慢走过太阳表面。天文学称这种现象为“金星凌日”。如图所示,2012年6月6日天空上演的“金星凌日”吸引了全世界数百万天文爱好者。假设地球公转轨道半径为R,“金星凌日”每隔t0年出现一次,则金星的公转轨道半径为( )
A. B.R
C.R D.R
4.所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。如图所示,是按课本要求用图钉和细绳画椭圆,这就可以形象地表示行星的轨道和太阳的位置。如果行星在C点的速率大于行星在B点的速率,则太阳应处在( )
A. B. C.都可以 D.无法判断
5.如图,地球绕太阳运动的轨道形状为椭圆,P为近日点,到太阳的距离为R1,Q点为远日点,到太阳的距离为,公转周期为T,月亮围绕地球做圆周运动,半径为r,公转周期为t。则( )
A.地球从P点运动到Q点的过程中,机械能变大
B.地球在P点和Q点的速率之比
C.相同时间内,月球与地球的连线扫过的面积等于地球与太阳连线扫过的面积
D.由开普勒第三定律可知,k为常数
6.17世纪,英国天文学家哈雷跟踪过一颗彗星,他算出这颗彗星轨道的半长轴约等于地球公转半径的18倍,并预言这颗彗星将每隔一定的时间飞临地球,后来哈雷的预言得到证实,该彗星被命名为哈雷彗星.哈雷彗星围绕太阳公转的轨道是一个非常扁的椭圆,如图所示.从公元前240年起,哈雷彗星每次回归,中国均有记录.它最近一次回归的时间是1986年.从公元前240年至今,我国关于哈雷彗星回归记录的次数,最合理的是
A.24次 B.30次 C.124次 D.319次
7.开普勒行星运动定律为万有引力定律的发现奠定了基础,根据开普勒定律,以下说法中正确的是( )
A.开普勒定律只适用于行星绕太阳的运动,不适用于卫星绕地球的运动
B.若某一人造地球卫星的轨道是椭圆,则地球处在该椭圆的一个焦点上
C.开普勒第三定律中的k值,不仅与中心天体有关,还与绕中心天体运动的行星(或卫星)有关
D.在探究太阳对行星的引力规律时,得到了开普勒第三定律,它是可以在实验室中得到证明的
8.如图所示,某卫星先在轨道1上绕地球做匀速圆周运动,周期为T,一段时间后,在P点变轨,进入椭圆转移轨道2,在远地点Q再变轨,进入圆轨道3,继续做匀速圆周运动,已知该卫星在轨道3上受到地球的引力为在轨道1上时所受地球引力的,不计卫星变轨过程中的质量损失,则卫星从P点运动到Q点所用的时间为( )
A.T B.T C.T D.T
9.某行星和地球绕太阳公转的轨道均可视为圆。每过N年,该行星会运行到日地连线的延长线上,如图所示该行星与地球的公转半径之比为( )
A. B. C. D.
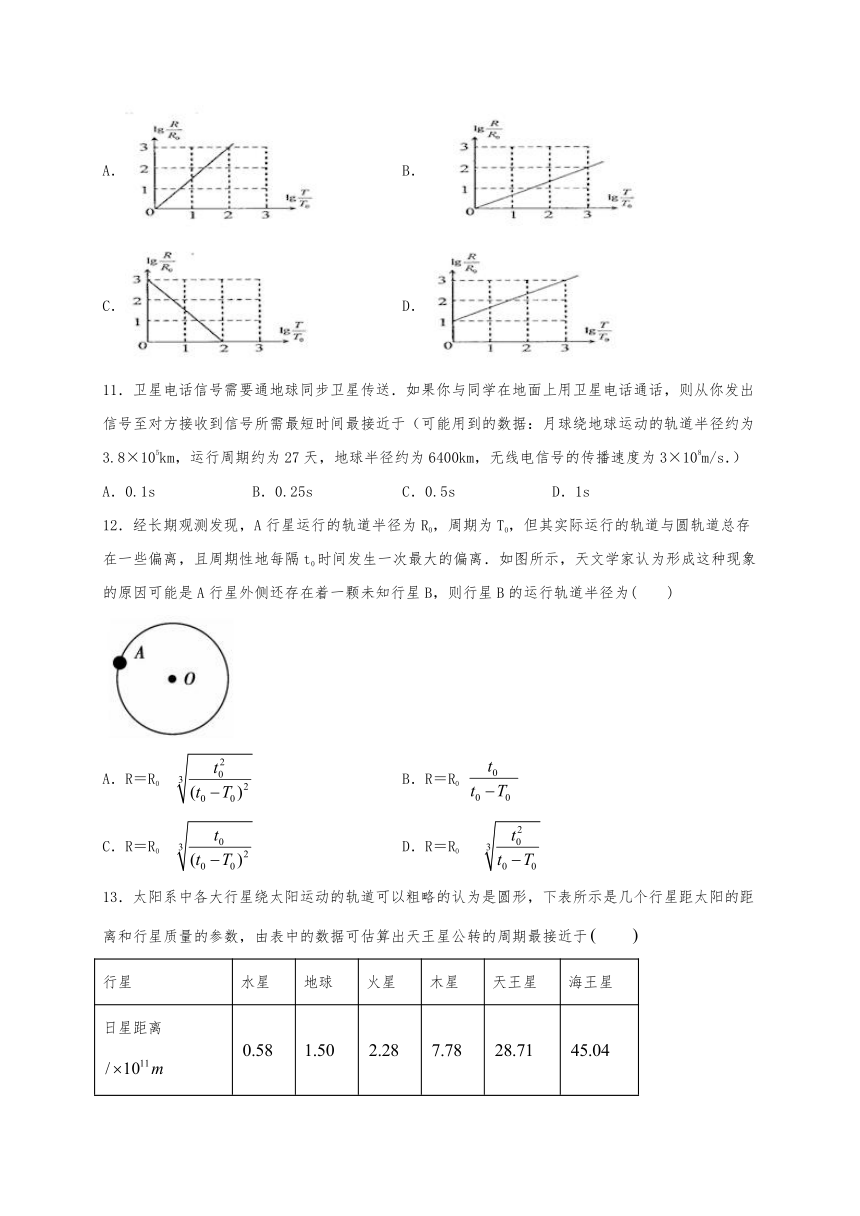
10.太阳系中的8大行星的轨道均可以近似看成圆轨道.下列4幅图是用来描述这些行星运动所遵从的某一规律的图像.图中坐标系的横轴是,纵轴是;这里T和R分别是行星绕太阳运行的周期和相应的圆轨道半径,和分别是水星绕太阳运行的周期和相应的圆轨道半径.下列4幅图中正确的是
A. B.
C. D.
11.卫星电话信号需要通地球同步卫星传送.如果你与同学在地面上用卫星电话通话,则从你发出信号至对方接收到信号所需最短时间最接近于(可能用到的数据:月球绕地球运动的轨道半径约为3.8×105km,运行周期约为27天,地球半径约为6400km,无线电信号的传播速度为3×108m/s.)
A.0.1s B.0.25s C.0.5s D.1s
12.经长期观测发现,A行星运行的轨道半径为R0,周期为T0,但其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.如图所示,天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则行星B的运行轨道半径为( )
A.R=R0 B.R=R0
C.R=R0 D.R=R0
13.太阳系中各大行星绕太阳运动的轨道可以粗略的认为是圆形,下表所示是几个行星距太阳的距离和行星质量的参数,由表中的数据可估算出天王星公转的周期最接近于
行星 水星 地球 火星 木星 天王星 海王星
日星距离
行星质量 1900 102
A.7000年 B.85年 C.20年 D.10年
14.如图所示,椭圆为某行星绕太阳运动的轨道,A、B分别为行星的近日点和远日点,行星经过这两点时的速率分别为vA和vB;阴影部分为行星与太阳的连线在相等时间内扫过的面积,分别用SA和SB表示.根据开普勒第二定律可知( )
A.vA>vB B.vA<vB C.SA>SB D.SA<SB
15.某行星绕太阳运行的椭圆轨道如图所示,F1和F2是椭圆轨道的两个焦点,行星在A点的速率比在B点的大,则太阳是位于( )
A.F1 B.F2 C.A D.B
16.近年来我国航天事业飞速发展,2020年7月23日,我国自主研发的火星探测器“天问一号”在海南文昌航天发射场由长征五号运载火箭发射升空,随后准确地进入预定地火转移轨道。如图所示为探测器经过多次变轨后登陆火星的轨迹示意图,其中轨道Ⅰ、Ⅲ为椭圆,轨道Ⅱ为圆。探测器经轨道Ⅰ、Ⅱ、Ⅲ运动后在Q点登陆火星,O点是轨道Ⅰ、Ⅱ、Ⅲ的交点,轨道上的O、P、Q三点与火星中心在同一直线上O、Q分别是椭圆轨道Ⅲ的远火星点和近火星点。已知火星的半径为R,,轨道Ⅱ上正常运行时经过O点的速度为v,关于探测器,下列说法正确的是( )
A.沿轨道Ⅰ运动时,探测器与Q点连线在相等时间内扫过的面积相等
B.沿轨道Ⅱ运动时,探测器经过O点的加速度大小等于
C.沿着轨道Ⅱ运行过程中,探测器于平衡状态
D.沿轨道Ⅱ的运动周期大于沿轨道Ⅰ的运动周期
二、解答题
17.太阳系各行星几乎在同一平面内沿同一方向绕太阳做圆周运动。当地球恰好运行到某地外行星和太阳之间,且三者几乎排成一条直线的现象,天文学称为“行星冲日”。已知地球及各地外行星绕太阳运动的轨道半径如下表所示。
地球 火星 木星 土星 天王星 海王星
轨道半径 1.0 1.5 5.2 9.5 19 30
根据题中信息,试计算
(1)火星相邻两次冲日的时间间隔。
(2)哪颗地外行星相邻两次冲日的时间间隔最长。
18.地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆。天文学家曾经跟踪过一颗彗星,假设这颗彗星轨道的半长轴约等于地球公转半径的9倍,并预言这颗彗星将每隔一定时间就会再次出现。
(1)若这颗彗星在近日点的线速度为,在远日点的线速度为,则哪个线速度大?
(2)如果这颗彗星最近出现的时间是2020年,它下次飞近地球大约是哪一年?
19.如图所示为地球绕太阳运动的示意图及春分、夏至、秋分、冬至时地球所在的位置。
(1)太阳是否在轨道平面的中心?夏至、冬至时地球到太阳的距离是否相同?
(2)一年之内秋、冬两季比春、夏两季为什么要少几天?
参考答案
1.A
【解析】设地球与太阳距离为r,根据题述可知木星与太阳的距离为R=
设木星的公转周期为T年,根据开普勒定律,则有
解得年
选项A正确;BCD错误;
故选A。
2.C
【解析】设彗星的公转周期为T1,地球的公转周期为T2,彗星的半长轴为r1,地球的公转半径为r2,由开普勒第三定律得
解得
它下次飞近地球大约是,1986+76=2062年。
故选C。
3.B
【解析】设金星的轨道半径为Rx,周期为Tx,角速度为ωx,则由开普勒第三定律有
可得
根据题意,应有ωx>ω0则(ωx-ω0)·t0=2π
即
解得,其中T0=1年
联立解得
故选B。
4.B
【解析】根据开普勒第二定律,对任意一个行星来说,它与太阳的连线在相等时间内扫过相等的面积。如果时间间隔相等,即,那么面积
即
得
如下图
由于
则有
即行星在在C点离太阳近,在B点离太阳远,所以太阳应处在点。
故选B。
5.B
【解析】A.地球围绕太阳运动,只有太阳的引力做功,机械能不变,故A错误;
B.由开普勒第二定律可知相同时间内,地球在近日点和远日点扫过的面积相等,由
所以
故B正确;
C.由开普勒第二定律可知,任意一个行星与太阳的连线在相等的时间内扫过的面积相等,必须是同一行星,故C错误;
D.由开普勒第三定律可知,所有行星的轨道半长轴的三次方跟它的公转周期的二次方的比值都相等,月亮不是行星,故D错误。
故选B。
6.B
【解析】
试题分析:本题考查的是开普勒第三定律,从而求出周期.设彗星的周期为,地球的公转周期为,由开普勒第三定律得到:,已知地球自转的周期,则可以求出,从公元前240年至1986年,即,所以最合理的次数是30次.故选项B正确
7.B
【解析】A.开普勒行星运动三定律不仅适用于行星绕太阳的运动,也适用于卫星绕地球的运动,故A错误;
B.根据开普勒第一定律,若人造地球卫星的轨道是椭圆,则地球在椭圆的一个焦点上,故B正确;
C.开普勒第三定律式中的k值,与中心天体的质量有关,与绕中心天体运动的行星(或卫星)无关,故C错误;
D.开普勒第三定律是开普勒在观察太阳系行星运动时得到的规律,在实验中不能验证,故D错误。
故选B。
8.D
【解析】由万有引力定律公式可知,轨道3的轨道半径是轨道1轨道半径的3倍,设轨道1的轨道半径为r,则轨道3的轨道半径为3r,椭圆轨道的半长轴为2r,设卫星从P点运动到Q点所用时间为t,则在椭圆轨道上运行的周期为2t,根据开普勒第三定律有
解得
故选D。
9.B
【解析】地球绕太阳公转周期年,N年转N周,而该行星由于轨道半径大,周期也大,因而该行星N年应转N-1周,故年
又因为行星和地球均绕太阳公转,由开普勒第三定律知
故
则B正确,ACD错误。
故选B。
10.B
【解析】由开普勒第三定律有=,则3=2,即3lg=2lg,因此lg-lg图线为过原点的斜率为的直线,故B项正确
11.B
【解析】同步卫星和月球都是地球的卫星,根据开普勒第三定律r3∝T2,因此同步卫星的轨道半径是地月距离的1/9约为42000km,同步卫星离地面高度约为36000km,电磁波往返一次经历时间约为(3.6×107×2)÷(3×108)s=0.24s
A.0.1s,与结论不相符,选项A错误;
B.0.25s,与结论相符,选项B正确;
C.0.5s,与结论不相符,选项C错误;
D.1s,与结论不相符,选项D错误;
故选B.
12.A
【解析】A行星运行的轨道发生最大偏离,必是B对A的引力引起的,B行星在此时刻对A有最大的力,故A、B行星与恒星在同一直线上且位于恒星同一侧.设行星B的运行周期为T,半径为R,则有t0-t0=2π,所以T=,由开普勒第三定律得,得R=R0 ,所以A正确.
13.B
【解析】天王星轨道半径是28.71×1011m,地球轨道半径是1.50×1011m;根据数据得天王星与地球的轨道半径之比大约为=18.7.根据万有引力提供向心力得解得:T=2π.则天王星与地球的周期之比大约为=85,因为地球的周期为1年,则天王星的周期大约为85年.故B正确,ACD错误.故选B.
14.A
【解析】
熟记理解开普勒的行星运动三定律:
第一定律:所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上.
第二定律:对每一个行星而言,太阳行星的连线在相同时间内扫过的面积相等.
第三定律:所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等.
【解析】C、D、对任意一个行星来说,它与太阳的连线在相等时间内扫过的面积相等,故有,C,D均错误.
A、B、A点和B点附近的面积近似为三角形的面积,有,因行星到太阳的连线,则可知vA>vB,故A正确,B错误.
故选A.
15.B
【解析】根据开普勒第二定律,太阳和行星的连线在相等时间内扫过的面积相同,可知,行星在近日点的速率大于远日点速率,所以A点是近日点,故太阳位于F2,故ACD错误,B正确。
故选B。
16.B
【解析】A.由开普勒定律可知,在同一轨道上运行的探测器与天体中心连线在相等时间内扫过的面积相等,而Q点并非天体中心位置,A错误;
B.轨道Ⅱ是圆轨道,半径为3R,经过O点的速度为v,根据圆周运动的规律可知,探测器经过O点的加速度
B正确;
C.沿着轨道Ⅱ运行过程中,受到火星的万有引力,加速度不为零,不是平衡态,C错误;
D.轨道Ⅱ的半径小于轨道Ⅰ的半长轴,由开普勒第三定律
可知,沿轨道Ⅱ的运动周期小于沿轨道Ⅰ运动周期,D错误。
故选B。
17.(1)2.2年;(2)火星
【解析】(1)由开普勒第三定律,其轨道半径的三次方与周期的平方的比值都相等,设地球绕太阳运行的周期为T,地球外另一行星的周期为,则两次冲日时间间隔为t,则
解得
对火星和地球
解得t=2.2T=2.2年
(2)根据
则越小,t越大,故地外行星中,火星相邻两次冲日的时间间隔最长。
18.(1)v1>v2;(2)2047
【解析】(1)彗星从近日点运动到远日点的过程中,引力做负功,动能减小,故近日点的线速度较大,即有v1>v2。也可通过开普勒第二定律判断知v1>v2。
(2)由开普勒第三定律知
得
解得年
即下次飞近地球大约为(2020+27)年=2047年
19.(1)不是,不相同;(2)秋、冬两季比春、夏两季地球运动的快
【解析】(1) 地球绕太阳的轨道是一个椭圆,太阳处于椭圆的焦点上,因此太阳不是在轨道平面的中心;由图可知,冬至离太阳的距离近,夏至离太阳的距离远,因此冬至和夏至到太阳的距离不相等。
(2) 由于在秋冬两季,地球处于近日点附近,根据开普勒第二定律,在相同的时间里面扫过相同的面积,因此,在秋冬两季,地球运动的较快,而在夏季,地球运动的较慢,因此秋、冬两季比春、夏两季要少几天。
一、单选题
1.位于贵州的“中国天眼”(FAST)是目前世界上口径最大的单天线射电望远镜,通过FAST可以测量地球与木星之间的距离。当FAST接收到来自木星的光线传播方向恰好与地球公转线速度方向相同时,测得地球与木星的距离是地球与太阳距离的k倍。若地球和木星绕太阳的运动均视为匀速圆周运动且轨道共面,则可知木星的公转周期为( )
A.年 B.年 C.年 D.年
2.地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆。天文学家哈雷曾经在1662年跟踪过一颗彗星,他算出这颗彗星轨道的半长轴约等于地球公转半径的18倍,并预言这颗彗星将每隔一定时间就会再次出现。这颗彗星最近出现的时间是1986年,它下次飞近地球大约是哪一年( )
A.2042年 B.2052年 C.2062年 D.2072年
3.设金星和地球绕太阳中心的运动是公转方向相同且轨道共面的匀速圆周运动,金星在地球轨道的内侧(称为地内行星)。在某些特殊时刻,地球、金星和太阳会出现在一条直线上,这时候从地球上观测,金星像镶嵌在太阳脸上的小黑痣缓慢走过太阳表面。天文学称这种现象为“金星凌日”。如图所示,2012年6月6日天空上演的“金星凌日”吸引了全世界数百万天文爱好者。假设地球公转轨道半径为R,“金星凌日”每隔t0年出现一次,则金星的公转轨道半径为( )
A. B.R
C.R D.R
4.所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。如图所示,是按课本要求用图钉和细绳画椭圆,这就可以形象地表示行星的轨道和太阳的位置。如果行星在C点的速率大于行星在B点的速率,则太阳应处在( )
A. B. C.都可以 D.无法判断
5.如图,地球绕太阳运动的轨道形状为椭圆,P为近日点,到太阳的距离为R1,Q点为远日点,到太阳的距离为,公转周期为T,月亮围绕地球做圆周运动,半径为r,公转周期为t。则( )
A.地球从P点运动到Q点的过程中,机械能变大
B.地球在P点和Q点的速率之比
C.相同时间内,月球与地球的连线扫过的面积等于地球与太阳连线扫过的面积
D.由开普勒第三定律可知,k为常数
6.17世纪,英国天文学家哈雷跟踪过一颗彗星,他算出这颗彗星轨道的半长轴约等于地球公转半径的18倍,并预言这颗彗星将每隔一定的时间飞临地球,后来哈雷的预言得到证实,该彗星被命名为哈雷彗星.哈雷彗星围绕太阳公转的轨道是一个非常扁的椭圆,如图所示.从公元前240年起,哈雷彗星每次回归,中国均有记录.它最近一次回归的时间是1986年.从公元前240年至今,我国关于哈雷彗星回归记录的次数,最合理的是
A.24次 B.30次 C.124次 D.319次
7.开普勒行星运动定律为万有引力定律的发现奠定了基础,根据开普勒定律,以下说法中正确的是( )
A.开普勒定律只适用于行星绕太阳的运动,不适用于卫星绕地球的运动
B.若某一人造地球卫星的轨道是椭圆,则地球处在该椭圆的一个焦点上
C.开普勒第三定律中的k值,不仅与中心天体有关,还与绕中心天体运动的行星(或卫星)有关
D.在探究太阳对行星的引力规律时,得到了开普勒第三定律,它是可以在实验室中得到证明的
8.如图所示,某卫星先在轨道1上绕地球做匀速圆周运动,周期为T,一段时间后,在P点变轨,进入椭圆转移轨道2,在远地点Q再变轨,进入圆轨道3,继续做匀速圆周运动,已知该卫星在轨道3上受到地球的引力为在轨道1上时所受地球引力的,不计卫星变轨过程中的质量损失,则卫星从P点运动到Q点所用的时间为( )
A.T B.T C.T D.T
9.某行星和地球绕太阳公转的轨道均可视为圆。每过N年,该行星会运行到日地连线的延长线上,如图所示该行星与地球的公转半径之比为( )
A. B. C. D.
10.太阳系中的8大行星的轨道均可以近似看成圆轨道.下列4幅图是用来描述这些行星运动所遵从的某一规律的图像.图中坐标系的横轴是,纵轴是;这里T和R分别是行星绕太阳运行的周期和相应的圆轨道半径,和分别是水星绕太阳运行的周期和相应的圆轨道半径.下列4幅图中正确的是
A. B.
C. D.
11.卫星电话信号需要通地球同步卫星传送.如果你与同学在地面上用卫星电话通话,则从你发出信号至对方接收到信号所需最短时间最接近于(可能用到的数据:月球绕地球运动的轨道半径约为3.8×105km,运行周期约为27天,地球半径约为6400km,无线电信号的传播速度为3×108m/s.)
A.0.1s B.0.25s C.0.5s D.1s
12.经长期观测发现,A行星运行的轨道半径为R0,周期为T0,但其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.如图所示,天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则行星B的运行轨道半径为( )
A.R=R0 B.R=R0
C.R=R0 D.R=R0
13.太阳系中各大行星绕太阳运动的轨道可以粗略的认为是圆形,下表所示是几个行星距太阳的距离和行星质量的参数,由表中的数据可估算出天王星公转的周期最接近于
行星 水星 地球 火星 木星 天王星 海王星
日星距离
行星质量 1900 102
A.7000年 B.85年 C.20年 D.10年
14.如图所示,椭圆为某行星绕太阳运动的轨道,A、B分别为行星的近日点和远日点,行星经过这两点时的速率分别为vA和vB;阴影部分为行星与太阳的连线在相等时间内扫过的面积,分别用SA和SB表示.根据开普勒第二定律可知( )
A.vA>vB B.vA<vB C.SA>SB D.SA<SB
15.某行星绕太阳运行的椭圆轨道如图所示,F1和F2是椭圆轨道的两个焦点,行星在A点的速率比在B点的大,则太阳是位于( )
A.F1 B.F2 C.A D.B
16.近年来我国航天事业飞速发展,2020年7月23日,我国自主研发的火星探测器“天问一号”在海南文昌航天发射场由长征五号运载火箭发射升空,随后准确地进入预定地火转移轨道。如图所示为探测器经过多次变轨后登陆火星的轨迹示意图,其中轨道Ⅰ、Ⅲ为椭圆,轨道Ⅱ为圆。探测器经轨道Ⅰ、Ⅱ、Ⅲ运动后在Q点登陆火星,O点是轨道Ⅰ、Ⅱ、Ⅲ的交点,轨道上的O、P、Q三点与火星中心在同一直线上O、Q分别是椭圆轨道Ⅲ的远火星点和近火星点。已知火星的半径为R,,轨道Ⅱ上正常运行时经过O点的速度为v,关于探测器,下列说法正确的是( )
A.沿轨道Ⅰ运动时,探测器与Q点连线在相等时间内扫过的面积相等
B.沿轨道Ⅱ运动时,探测器经过O点的加速度大小等于
C.沿着轨道Ⅱ运行过程中,探测器于平衡状态
D.沿轨道Ⅱ的运动周期大于沿轨道Ⅰ的运动周期
二、解答题
17.太阳系各行星几乎在同一平面内沿同一方向绕太阳做圆周运动。当地球恰好运行到某地外行星和太阳之间,且三者几乎排成一条直线的现象,天文学称为“行星冲日”。已知地球及各地外行星绕太阳运动的轨道半径如下表所示。
地球 火星 木星 土星 天王星 海王星
轨道半径 1.0 1.5 5.2 9.5 19 30
根据题中信息,试计算
(1)火星相邻两次冲日的时间间隔。
(2)哪颗地外行星相邻两次冲日的时间间隔最长。
18.地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆。天文学家曾经跟踪过一颗彗星,假设这颗彗星轨道的半长轴约等于地球公转半径的9倍,并预言这颗彗星将每隔一定时间就会再次出现。
(1)若这颗彗星在近日点的线速度为,在远日点的线速度为,则哪个线速度大?
(2)如果这颗彗星最近出现的时间是2020年,它下次飞近地球大约是哪一年?
19.如图所示为地球绕太阳运动的示意图及春分、夏至、秋分、冬至时地球所在的位置。
(1)太阳是否在轨道平面的中心?夏至、冬至时地球到太阳的距离是否相同?
(2)一年之内秋、冬两季比春、夏两季为什么要少几天?
参考答案
1.A
【解析】设地球与太阳距离为r,根据题述可知木星与太阳的距离为R=
设木星的公转周期为T年,根据开普勒定律,则有
解得年
选项A正确;BCD错误;
故选A。
2.C
【解析】设彗星的公转周期为T1,地球的公转周期为T2,彗星的半长轴为r1,地球的公转半径为r2,由开普勒第三定律得
解得
它下次飞近地球大约是,1986+76=2062年。
故选C。
3.B
【解析】设金星的轨道半径为Rx,周期为Tx,角速度为ωx,则由开普勒第三定律有
可得
根据题意,应有ωx>ω0则(ωx-ω0)·t0=2π
即
解得,其中T0=1年
联立解得
故选B。
4.B
【解析】根据开普勒第二定律,对任意一个行星来说,它与太阳的连线在相等时间内扫过相等的面积。如果时间间隔相等,即,那么面积
即
得
如下图
由于
则有
即行星在在C点离太阳近,在B点离太阳远,所以太阳应处在点。
故选B。
5.B
【解析】A.地球围绕太阳运动,只有太阳的引力做功,机械能不变,故A错误;
B.由开普勒第二定律可知相同时间内,地球在近日点和远日点扫过的面积相等,由
所以
故B正确;
C.由开普勒第二定律可知,任意一个行星与太阳的连线在相等的时间内扫过的面积相等,必须是同一行星,故C错误;
D.由开普勒第三定律可知,所有行星的轨道半长轴的三次方跟它的公转周期的二次方的比值都相等,月亮不是行星,故D错误。
故选B。
6.B
【解析】
试题分析:本题考查的是开普勒第三定律,从而求出周期.设彗星的周期为,地球的公转周期为,由开普勒第三定律得到:,已知地球自转的周期,则可以求出,从公元前240年至1986年,即,所以最合理的次数是30次.故选项B正确
7.B
【解析】A.开普勒行星运动三定律不仅适用于行星绕太阳的运动,也适用于卫星绕地球的运动,故A错误;
B.根据开普勒第一定律,若人造地球卫星的轨道是椭圆,则地球在椭圆的一个焦点上,故B正确;
C.开普勒第三定律式中的k值,与中心天体的质量有关,与绕中心天体运动的行星(或卫星)无关,故C错误;
D.开普勒第三定律是开普勒在观察太阳系行星运动时得到的规律,在实验中不能验证,故D错误。
故选B。
8.D
【解析】由万有引力定律公式可知,轨道3的轨道半径是轨道1轨道半径的3倍,设轨道1的轨道半径为r,则轨道3的轨道半径为3r,椭圆轨道的半长轴为2r,设卫星从P点运动到Q点所用时间为t,则在椭圆轨道上运行的周期为2t,根据开普勒第三定律有
解得
故选D。
9.B
【解析】地球绕太阳公转周期年,N年转N周,而该行星由于轨道半径大,周期也大,因而该行星N年应转N-1周,故年
又因为行星和地球均绕太阳公转,由开普勒第三定律知
故
则B正确,ACD错误。
故选B。
10.B
【解析】由开普勒第三定律有=,则3=2,即3lg=2lg,因此lg-lg图线为过原点的斜率为的直线,故B项正确
11.B
【解析】同步卫星和月球都是地球的卫星,根据开普勒第三定律r3∝T2,因此同步卫星的轨道半径是地月距离的1/9约为42000km,同步卫星离地面高度约为36000km,电磁波往返一次经历时间约为(3.6×107×2)÷(3×108)s=0.24s
A.0.1s,与结论不相符,选项A错误;
B.0.25s,与结论相符,选项B正确;
C.0.5s,与结论不相符,选项C错误;
D.1s,与结论不相符,选项D错误;
故选B.
12.A
【解析】A行星运行的轨道发生最大偏离,必是B对A的引力引起的,B行星在此时刻对A有最大的力,故A、B行星与恒星在同一直线上且位于恒星同一侧.设行星B的运行周期为T,半径为R,则有t0-t0=2π,所以T=,由开普勒第三定律得,得R=R0 ,所以A正确.
13.B
【解析】天王星轨道半径是28.71×1011m,地球轨道半径是1.50×1011m;根据数据得天王星与地球的轨道半径之比大约为=18.7.根据万有引力提供向心力得解得:T=2π.则天王星与地球的周期之比大约为=85,因为地球的周期为1年,则天王星的周期大约为85年.故B正确,ACD错误.故选B.
14.A
【解析】
熟记理解开普勒的行星运动三定律:
第一定律:所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上.
第二定律:对每一个行星而言,太阳行星的连线在相同时间内扫过的面积相等.
第三定律:所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等.
【解析】C、D、对任意一个行星来说,它与太阳的连线在相等时间内扫过的面积相等,故有,C,D均错误.
A、B、A点和B点附近的面积近似为三角形的面积,有,因行星到太阳的连线,则可知vA>vB,故A正确,B错误.
故选A.
15.B
【解析】根据开普勒第二定律,太阳和行星的连线在相等时间内扫过的面积相同,可知,行星在近日点的速率大于远日点速率,所以A点是近日点,故太阳位于F2,故ACD错误,B正确。
故选B。
16.B
【解析】A.由开普勒定律可知,在同一轨道上运行的探测器与天体中心连线在相等时间内扫过的面积相等,而Q点并非天体中心位置,A错误;
B.轨道Ⅱ是圆轨道,半径为3R,经过O点的速度为v,根据圆周运动的规律可知,探测器经过O点的加速度
B正确;
C.沿着轨道Ⅱ运行过程中,受到火星的万有引力,加速度不为零,不是平衡态,C错误;
D.轨道Ⅱ的半径小于轨道Ⅰ的半长轴,由开普勒第三定律
可知,沿轨道Ⅱ的运动周期小于沿轨道Ⅰ运动周期,D错误。
故选B。
17.(1)2.2年;(2)火星
【解析】(1)由开普勒第三定律,其轨道半径的三次方与周期的平方的比值都相等,设地球绕太阳运行的周期为T,地球外另一行星的周期为,则两次冲日时间间隔为t,则
解得
对火星和地球
解得t=2.2T=2.2年
(2)根据
则越小,t越大,故地外行星中,火星相邻两次冲日的时间间隔最长。
18.(1)v1>v2;(2)2047
【解析】(1)彗星从近日点运动到远日点的过程中,引力做负功,动能减小,故近日点的线速度较大,即有v1>v2。也可通过开普勒第二定律判断知v1>v2。
(2)由开普勒第三定律知
得
解得年
即下次飞近地球大约为(2020+27)年=2047年
19.(1)不是,不相同;(2)秋、冬两季比春、夏两季地球运动的快
【解析】(1) 地球绕太阳的轨道是一个椭圆,太阳处于椭圆的焦点上,因此太阳不是在轨道平面的中心;由图可知,冬至离太阳的距离近,夏至离太阳的距离远,因此冬至和夏至到太阳的距离不相等。
(2) 由于在秋冬两季,地球处于近日点附近,根据开普勒第二定律,在相同的时间里面扫过相同的面积,因此,在秋冬两季,地球运动的较快,而在夏季,地球运动的较慢,因此秋、冬两季比春、夏两季要少几天。
