18.1.1平行四边形的性质课件(29张)
文档属性
| 名称 | 18.1.1平行四边形的性质课件(29张) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-24 07:06:25 | ||
图片预览




文档简介
人教版数学八年级下册
18.1.1 平行四边形的性质(1)
学习目标
1.理解并掌握平行四边形的概念和平行四边形对边、
对角相等的性质.重点
2.会用平行四边形的性质解决简单的平行四边形的
计算问题,并会进行有关的论证. 难点
3.培养学生发现问题、解决问题的能力及逻辑推理能力.
欣赏图片
观察这些图片,它们是否都有平行四边形的形象?
你还记得平行四边形的定义吗?
探索新知
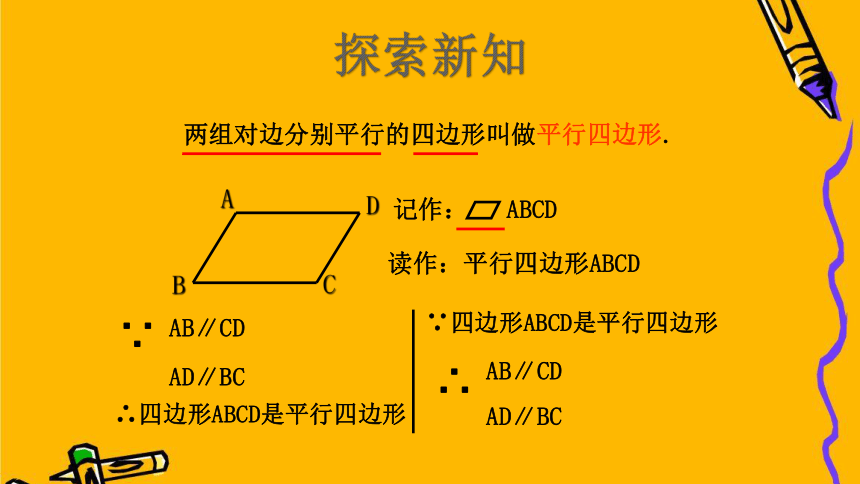
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
探索新知
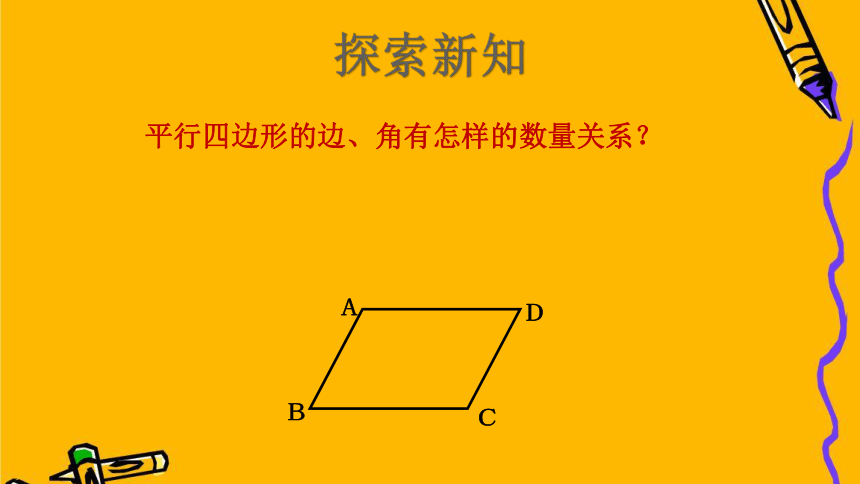
平行四边形的边、角有怎样的数量关系?
A
B
C
D
探索新知
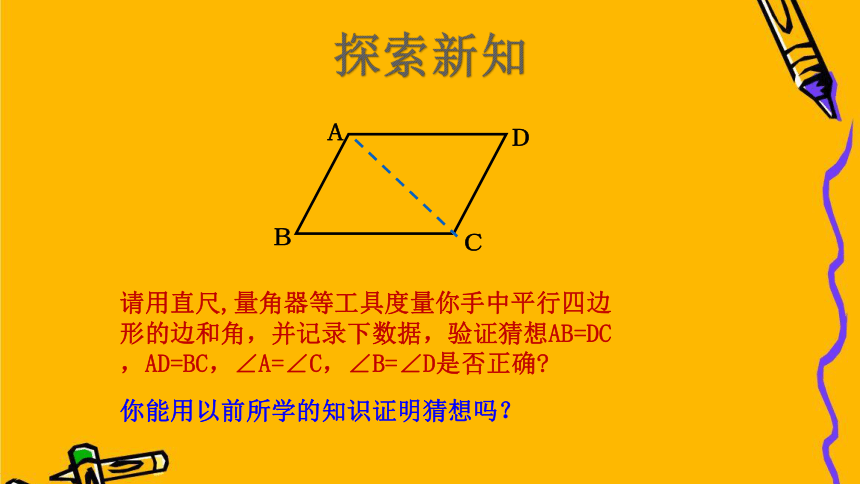
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确?
A
B
C
D
你能用以前所学的知识证明猜想吗?
探索新知
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题.
探索新知
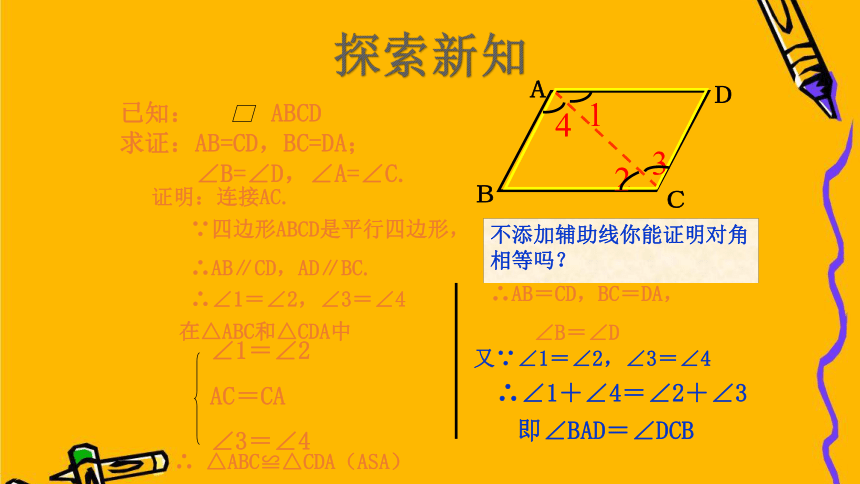
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
A
B
C
D
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC.
不添加辅助线你能证明对角相等吗?
探索新知
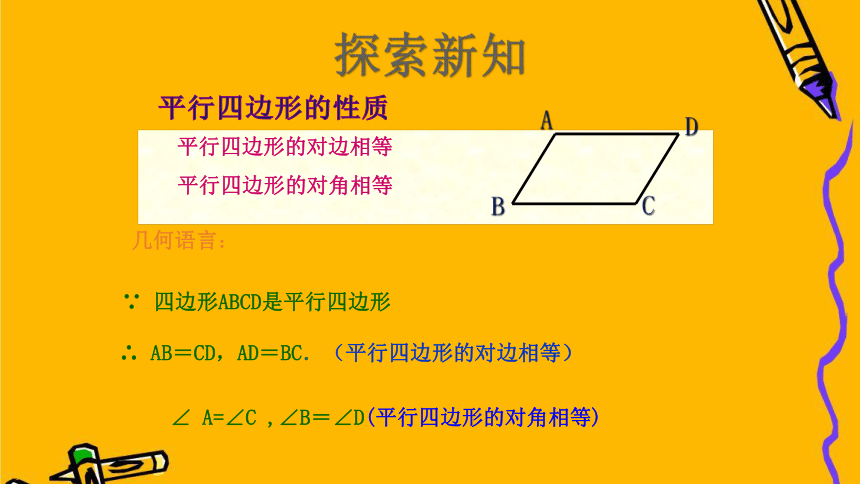
平行四边形的性质
几何语言:
平行四边形的对边相等
平行四边形的对角相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
∠ A=∠C ,∠B=∠D(平行四边形的对角相等)
A
D
B
C
探索新知
H
A
B
C
D
G
若a // b,作 AD // GH // BC,分别交 b于D、H、C,交 a于A、G、B.
两条平行线间的距离
则 GH=AD=BC.
两条平行线之间的平行线段相等
则 DA HG CB.
(应用性质1)
若a // b,DA、GH、CB垂直于 a,交a于A、G、B,交 b于D、H、C.
b
a
A
B
C
D
a
b
H
G
点到直线的距离
=
=
相等
典型例题
例1 在平行四边形ABCD中,
垂足分别为
求证 .
A
B
D
C
E
F
基础训练
1.在□ ABCD中,∠A:∠B=2:3,则∠A= _____ ,∠B= ______,∠C= ______, ∠D= _______.
2.已知□ ABCD的周长为20cm,且AD-AB=1cm,则 AD= ______,CD= ______ .
5.5cm
4.5cm
基础训练
3.判断题:(对的在括号内填“√”,错的填“×”)
(1)平行四边形两组对边分别平行且相等. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°( )
(4)如果平行四边形相邻两边长分别是2cm和
3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=42°,
那么∠B=48°. ( )
√
×
√
√
×
基础训练
4.在 ABCD中, AB=3cm,BC=8cm,则 ABCD的周长
是 cm.
5. ABCD的周长为30cm,两邻边之比为2﹕1,则 ABCD
的两邻边长分别为 .
6. ABCD的周长为30cm,AB比BC长5cm,则AB= cm,
CD= cm.
7.如图,在 ABCD中,∠B的平分线BE交AD于E,BC=5,
AB=3,则ED的长为 .
22
10cm,5cm
2
10
10
基础训练
8、如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形。转动其中一张纸条,线段AD和BC的长度有什么关系?为什么?
解:AD和BC的长度相等
证明:由题可知,AB//CD,AD//BC
∴四边形ABCD是 ABCD
∴AD=BC
基础训练
9、求如图所示的平行四边形的面积.
解:如图:在 ABCD中,
∵CD=3 ∴AB=3
在△ABC中AB+AC=BC
由勾股定理知, △ABC是Rt △ABC
∴ AB x AC= BC x AE
既 x 3 x 4=5 x AE ∴AE=
∴S ABCD=5 x =12
E
2
1
—
2
12
—
5
2
2
1
—
2
1
—
2
12
—
5
基础训练
10.如图,在 ABCD中, AB=10,AD=8,AC⊥
BC. 求BC,CD,AC,OA的长,以及 ABCD的面积.
A
B
C
D
O
课堂小结
1. 概念:
四边形
两组对边
平行四边形
分别平行
2. 性质:
性质一:对边平行,相等;
性质二:对角相等,邻角互补.
3. 两平行线之间的距离相等.
课堂作业
课堂作业
课堂作业
7.△ABC是等腰三角形,AB=AC, P是底边BC
上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB
上.求证:PE+PF=AB.
A
B
C
E
F
P
课堂作业
4.C 5.B 6.B
1.平行四边形 2.B 3.A
课堂作业
8.如图,已知四边形ABCD是平行四边形,
点E、B、D、F在同一直线上,且BE=DF.
求证:AE=CF.
课堂作业
8.
课后思考
1.已知□ABCD的周长为36 cm,过点A作AE⊥BC,
AF⊥CD,若AE=2 cm,AF=4 cm,求平行四边形
的各边长.
课后思考
用面积法.
∵AE·BC=CD·AF,∴BC=2CD.
∵ABCD为平行四边形,
∴AB=CD,BC=AD.
∴□ABCD周长为:2(BC+CD)=6CD=36 cm.
∴AB=CD=6 cm,BC=AD=12 cm.
1.
课后思考
2.如图,四边形ABCD是平行四边形,P是CD上
一点,且AP和BP分别平分∠DAB和∠CBA.
(1)求∠APB的度数;
(2)如果AD=5 cm,AP=8 cm,求△APB的周长.
课后思考
2.(1)∠APB=90°.
(2)△APB的周长是24 cm.
再见
18.1.1 平行四边形的性质(1)
学习目标
1.理解并掌握平行四边形的概念和平行四边形对边、
对角相等的性质.重点
2.会用平行四边形的性质解决简单的平行四边形的
计算问题,并会进行有关的论证. 难点
3.培养学生发现问题、解决问题的能力及逻辑推理能力.
欣赏图片
观察这些图片,它们是否都有平行四边形的形象?
你还记得平行四边形的定义吗?
探索新知
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
探索新知
平行四边形的边、角有怎样的数量关系?
A
B
C
D
探索新知
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确?
A
B
C
D
你能用以前所学的知识证明猜想吗?
探索新知
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题.
探索新知
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
A
B
C
D
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC.
不添加辅助线你能证明对角相等吗?
探索新知
平行四边形的性质
几何语言:
平行四边形的对边相等
平行四边形的对角相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
∠ A=∠C ,∠B=∠D(平行四边形的对角相等)
A
D
B
C
探索新知
H
A
B
C
D
G
若a // b,作 AD // GH // BC,分别交 b于D、H、C,交 a于A、G、B.
两条平行线间的距离
则 GH=AD=BC.
两条平行线之间的平行线段相等
则 DA HG CB.
(应用性质1)
若a // b,DA、GH、CB垂直于 a,交a于A、G、B,交 b于D、H、C.
b
a
A
B
C
D
a
b
H
G
点到直线的距离
=
=
相等
典型例题
例1 在平行四边形ABCD中,
垂足分别为
求证 .
A
B
D
C
E
F
基础训练
1.在□ ABCD中,∠A:∠B=2:3,则∠A= _____ ,∠B= ______,∠C= ______, ∠D= _______.
2.已知□ ABCD的周长为20cm,且AD-AB=1cm,则 AD= ______,CD= ______ .
5.5cm
4.5cm
基础训练
3.判断题:(对的在括号内填“√”,错的填“×”)
(1)平行四边形两组对边分别平行且相等. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°( )
(4)如果平行四边形相邻两边长分别是2cm和
3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=42°,
那么∠B=48°. ( )
√
×
√
√
×
基础训练
4.在 ABCD中, AB=3cm,BC=8cm,则 ABCD的周长
是 cm.
5. ABCD的周长为30cm,两邻边之比为2﹕1,则 ABCD
的两邻边长分别为 .
6. ABCD的周长为30cm,AB比BC长5cm,则AB= cm,
CD= cm.
7.如图,在 ABCD中,∠B的平分线BE交AD于E,BC=5,
AB=3,则ED的长为 .
22
10cm,5cm
2
10
10
基础训练
8、如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形。转动其中一张纸条,线段AD和BC的长度有什么关系?为什么?
解:AD和BC的长度相等
证明:由题可知,AB//CD,AD//BC
∴四边形ABCD是 ABCD
∴AD=BC
基础训练
9、求如图所示的平行四边形的面积.
解:如图:在 ABCD中,
∵CD=3 ∴AB=3
在△ABC中AB+AC=BC
由勾股定理知, △ABC是Rt △ABC
∴ AB x AC= BC x AE
既 x 3 x 4=5 x AE ∴AE=
∴S ABCD=5 x =12
E
2
1
—
2
12
—
5
2
2
1
—
2
1
—
2
12
—
5
基础训练
10.如图,在 ABCD中, AB=10,AD=8,AC⊥
BC. 求BC,CD,AC,OA的长,以及 ABCD的面积.
A
B
C
D
O
课堂小结
1. 概念:
四边形
两组对边
平行四边形
分别平行
2. 性质:
性质一:对边平行,相等;
性质二:对角相等,邻角互补.
3. 两平行线之间的距离相等.
课堂作业
课堂作业
课堂作业
7.△ABC是等腰三角形,AB=AC, P是底边BC
上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB
上.求证:PE+PF=AB.
A
B
C
E
F
P
课堂作业
4.C 5.B 6.B
1.平行四边形 2.B 3.A
课堂作业
8.如图,已知四边形ABCD是平行四边形,
点E、B、D、F在同一直线上,且BE=DF.
求证:AE=CF.
课堂作业
8.
课后思考
1.已知□ABCD的周长为36 cm,过点A作AE⊥BC,
AF⊥CD,若AE=2 cm,AF=4 cm,求平行四边形
的各边长.
课后思考
用面积法.
∵AE·BC=CD·AF,∴BC=2CD.
∵ABCD为平行四边形,
∴AB=CD,BC=AD.
∴□ABCD周长为:2(BC+CD)=6CD=36 cm.
∴AB=CD=6 cm,BC=AD=12 cm.
1.
课后思考
2.如图,四边形ABCD是平行四边形,P是CD上
一点,且AP和BP分别平分∠DAB和∠CBA.
(1)求∠APB的度数;
(2)如果AD=5 cm,AP=8 cm,求△APB的周长.
课后思考
2.(1)∠APB=90°.
(2)△APB的周长是24 cm.
再见
