专题 表面积与体积的求解 - 2020-2021学年高一下学期人教A版(2019)必修第二册(26张PPT)
文档属性
| 名称 | 专题 表面积与体积的求解 - 2020-2021学年高一下学期人教A版(2019)必修第二册(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-23 11:36:02 | ||
图片预览




文档简介
专题 表面积与体积的求解
第八章 几何初步
学习目标
XUE XI MU BIAO
1.掌握多面体和旋转体的表面积和体积计算.
2.掌握简单组合体的表面积和体积的计算.
知识梳理
题型探究
随堂演练
{5940675A-B579-460E-94D1-54222C63F5DA}几何体
面积公式
直棱柱侧面积
S直棱柱侧=ch .
正棱锥侧面积
S正棱锥侧=ch′.
正棱台侧面积
S正棱台侧=(c+c′)h′.
圆柱侧面积
S圆柱侧=cl=2πrl.
圆锥侧面积
S圆锥侧=cl=πrl.
圆台侧面积
S圆台侧=(c+c′)l=π(r+r′)l.
圆柱表面积
S圆柱表面积=2πr2+2πrl=2πr(r+l)
圆锥表面积
S圆锥表面积=πr2+πrl=πr(r+l)
圆台表面积
S圆台表面积=π(r′2+r2+r′l+rl)
球的表面积
S球的表面积=4πR2
{5940675A-B579-460E-94D1-54222C63F5DA}几何体
体积公式
柱体
V=Sh(S为底面面积,h为柱体的高)
锥体
V=Sh(S为底面面积,h为锥体的高)
台体
V=(S′+ +S)h(S′、S分别为上、下底面面积,h为台体的高)
球体
V球= πR3(其中R为球的半径)
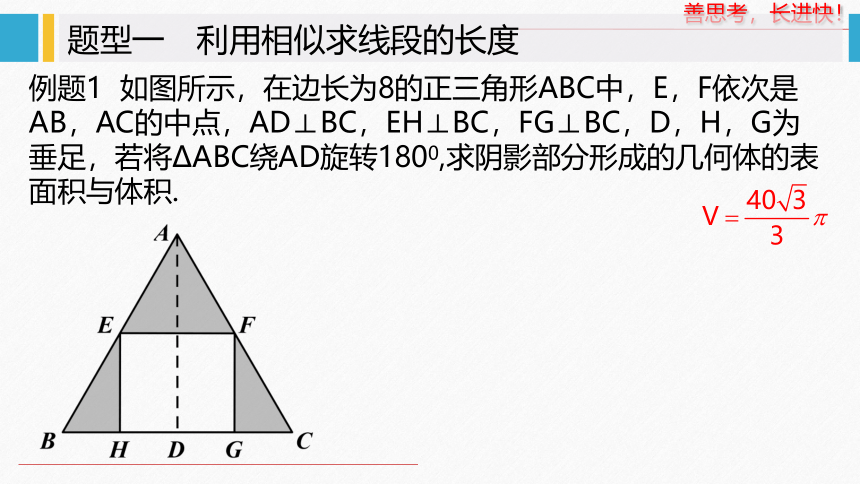
题型一 利用相似求线段的长度
例题1 如图所示,在边长为8的正三角形ABC中,E,F依次是AB,AC的中点,AD⊥BC,EH⊥BC,FG⊥BC,D,H,G为垂足,若将ΔABC绕AD旋转1800,求阴影部分形成的几何体的表面积与体积.
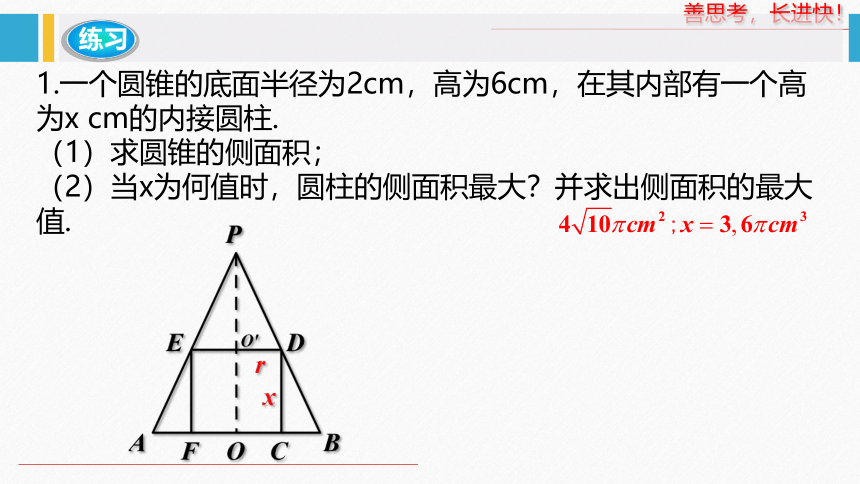
练习
1.一个圆锥的底面半径为2cm,高为6cm,在其内部有一个高为x cm的内接圆柱.
(1)求圆锥的侧面积;
(2)当x为何值时,圆柱的侧面积最大?并求出侧面积的最大值.
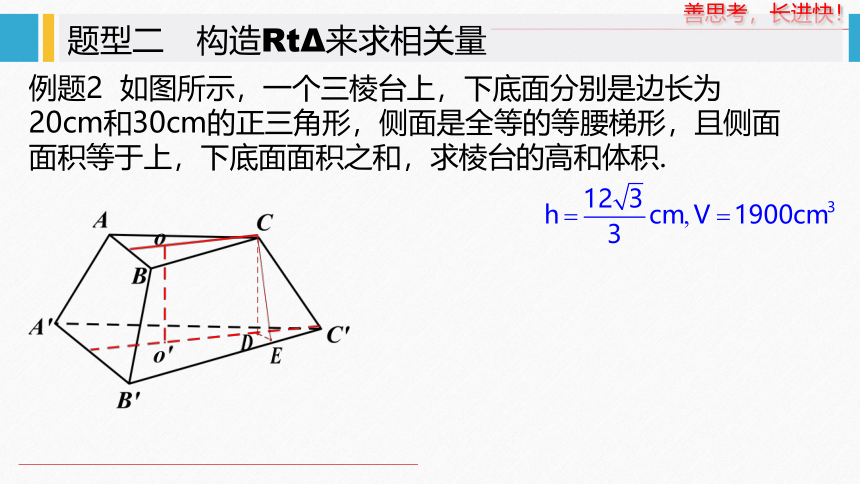
题型二 构造RtΔ来求相关量
例题2 如图所示,一个三棱台上,下底面分别是边长为20cm和30cm的正三角形,侧面是全等的等腰梯形,且侧面面积等于上,下底面面积之和,求棱台的高和体积.
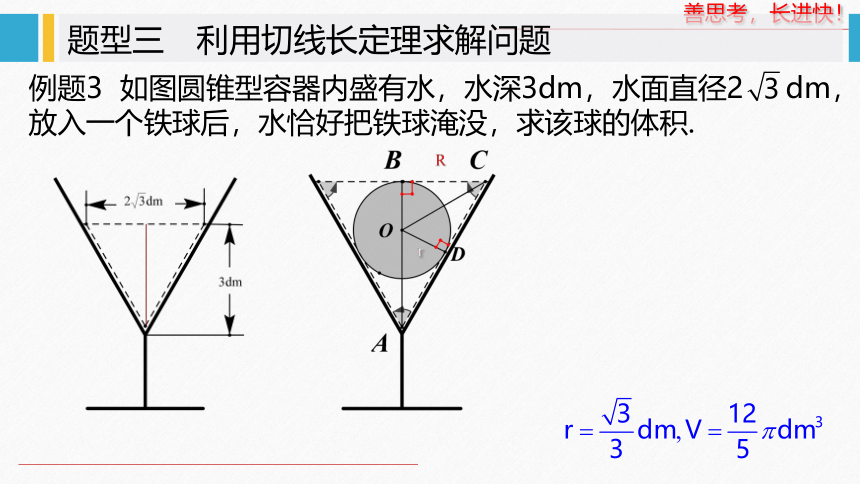
题型三 利用切线长定理求解问题
例题3 如图圆锥型容器内盛有水,水深3dm,水面直径2 dm,放入一个铁球后,水恰好把铁球淹没,求该球的体积.
练习
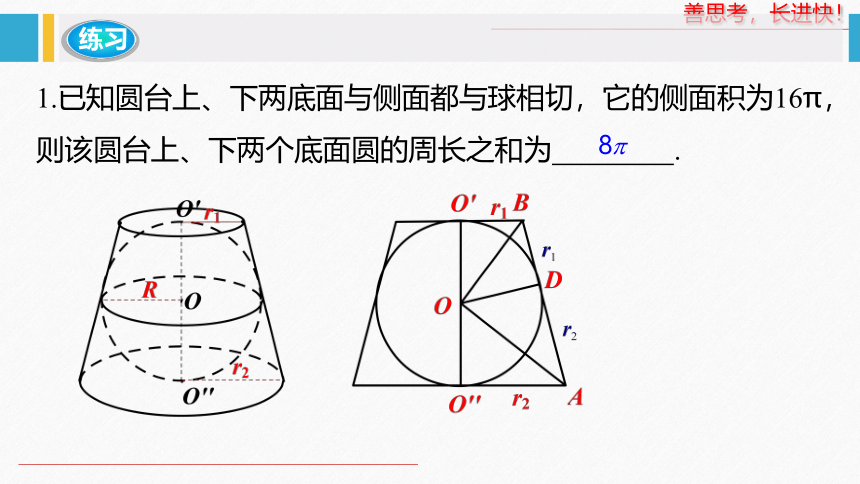
1.已知圆台上、下两底面与侧面都与球相切,它的侧面积为16π,则该圆台上、下两个底面圆的周长之和为 .
题型四 与三视图的结合
例题4 一个多面体是由正方体割去两个三棱锥得到的,其正视图、侧视图、俯视图均是边长为2的正方形,如图所示,该多面体的表面积是( )
A. B. C. D.
练习
1.某圆锥的三视图如图,△ABC是边长为2的等边三角形,P为AB的中点,三视图中的点C,P分别对应圆锥中的点M,N,则在圆锥侧面展开图中M,N之间的距离为 .
例题5 已知球的两平行截面的面积为5π和8π,它们位于球心的同侧,且相距为 1 ,求这个球的表面积.
题型五 与截面有关的问题
练习
1.如图,半径为6的球的两个内接圆锥有公共的底面,若两个圆锥的体积之和为球的体积的 ,则这两个圆锥高之差的绝对值为( )
A.2 B.4
C.6 D.8
例题6 设P,A,B,C是球O表面上的四个点,若PA⊥PB,PB⊥PC,PA⊥PC,且PA=PB=PC=2,则球O的体积为( )
A.48π B. C.12π D.
题型六 几何体与球的切接问题
练习
1.已知正四面体A'-BDC'外接球的表面积为12π,则该正四面体的表面积为( )A. B. C. D.
练习
2.正三棱柱的底面边长为 ,侧棱长为2,且三棱柱的顶点都在同一个球面上,则该球的表面积为 .
练习
3.已知圆柱的高为1,它的两个底面的圆周在直径长为2的同一个球面上,则该圆柱体的体积为( )
A. B.
C. D.
练习
4.一个球与它的外切圆柱、外切等边圆锥(圆锥的轴截面为正三角形)的体积之比( )
A.2∶3∶5 B.2∶3∶4 C.3∶5∶8 D.4∶6∶9
例题7 已知R的球面上有A、B两点,它们的球面距离是 R,则线段AB的长为( )
A. B.
C. D.
练习
5.已知球面上两点A,B之间的球面距离为4π,过这两点的两条球半径之间的夹角为60°,以AB为直径的球的小圆的面积为_____________.
例题8 如图,三棱柱ABC—A'B'C'中,若E、F分别为AB、AC 的中点,平面EB'C'将三棱柱分成体积为V1、V2的两部分,那么V1:V2=_____ .
题型七 几何体的割补求体积问题
1.如图,将一个长方体用过相邻三条棱中点的平面截出一个棱锥,则该棱锥的体积与剩下的几何体的体积的比是______.
练习
例题9 如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现,圆柱的体积与球的体积之比为 ,圆柱的表面积与球的表面积之比为 .
题型八 数学史
1.木星的表面积约是地球的120倍,体积约是地球的____ __倍.
练习
2.我国古代数学名著《九章算术?商功》中将底面是直角三角形的直三棱柱称之为“堑堵”,如图为一个堑堵ABC﹣DFE,AB⊥BC,AB=6,其体积为120,若将该“堑堵”放入一个球形容器中,则该球形容器表面积的最小值为( )
A.100π B.108π
C.116π D.120π
谢谢!
第八章 几何初步
学习目标
XUE XI MU BIAO
1.掌握多面体和旋转体的表面积和体积计算.
2.掌握简单组合体的表面积和体积的计算.
知识梳理
题型探究
随堂演练
{5940675A-B579-460E-94D1-54222C63F5DA}几何体
面积公式
直棱柱侧面积
S直棱柱侧=ch .
正棱锥侧面积
S正棱锥侧=ch′.
正棱台侧面积
S正棱台侧=(c+c′)h′.
圆柱侧面积
S圆柱侧=cl=2πrl.
圆锥侧面积
S圆锥侧=cl=πrl.
圆台侧面积
S圆台侧=(c+c′)l=π(r+r′)l.
圆柱表面积
S圆柱表面积=2πr2+2πrl=2πr(r+l)
圆锥表面积
S圆锥表面积=πr2+πrl=πr(r+l)
圆台表面积
S圆台表面积=π(r′2+r2+r′l+rl)
球的表面积
S球的表面积=4πR2
{5940675A-B579-460E-94D1-54222C63F5DA}几何体
体积公式
柱体
V=Sh(S为底面面积,h为柱体的高)
锥体
V=Sh(S为底面面积,h为锥体的高)
台体
V=(S′+ +S)h(S′、S分别为上、下底面面积,h为台体的高)
球体
V球= πR3(其中R为球的半径)
题型一 利用相似求线段的长度
例题1 如图所示,在边长为8的正三角形ABC中,E,F依次是AB,AC的中点,AD⊥BC,EH⊥BC,FG⊥BC,D,H,G为垂足,若将ΔABC绕AD旋转1800,求阴影部分形成的几何体的表面积与体积.
练习
1.一个圆锥的底面半径为2cm,高为6cm,在其内部有一个高为x cm的内接圆柱.
(1)求圆锥的侧面积;
(2)当x为何值时,圆柱的侧面积最大?并求出侧面积的最大值.
题型二 构造RtΔ来求相关量
例题2 如图所示,一个三棱台上,下底面分别是边长为20cm和30cm的正三角形,侧面是全等的等腰梯形,且侧面面积等于上,下底面面积之和,求棱台的高和体积.
题型三 利用切线长定理求解问题
例题3 如图圆锥型容器内盛有水,水深3dm,水面直径2 dm,放入一个铁球后,水恰好把铁球淹没,求该球的体积.
练习
1.已知圆台上、下两底面与侧面都与球相切,它的侧面积为16π,则该圆台上、下两个底面圆的周长之和为 .
题型四 与三视图的结合
例题4 一个多面体是由正方体割去两个三棱锥得到的,其正视图、侧视图、俯视图均是边长为2的正方形,如图所示,该多面体的表面积是( )
A. B. C. D.
练习
1.某圆锥的三视图如图,△ABC是边长为2的等边三角形,P为AB的中点,三视图中的点C,P分别对应圆锥中的点M,N,则在圆锥侧面展开图中M,N之间的距离为 .
例题5 已知球的两平行截面的面积为5π和8π,它们位于球心的同侧,且相距为 1 ,求这个球的表面积.
题型五 与截面有关的问题
练习
1.如图,半径为6的球的两个内接圆锥有公共的底面,若两个圆锥的体积之和为球的体积的 ,则这两个圆锥高之差的绝对值为( )
A.2 B.4
C.6 D.8
例题6 设P,A,B,C是球O表面上的四个点,若PA⊥PB,PB⊥PC,PA⊥PC,且PA=PB=PC=2,则球O的体积为( )
A.48π B. C.12π D.
题型六 几何体与球的切接问题
练习
1.已知正四面体A'-BDC'外接球的表面积为12π,则该正四面体的表面积为( )A. B. C. D.
练习
2.正三棱柱的底面边长为 ,侧棱长为2,且三棱柱的顶点都在同一个球面上,则该球的表面积为 .
练习
3.已知圆柱的高为1,它的两个底面的圆周在直径长为2的同一个球面上,则该圆柱体的体积为( )
A. B.
C. D.
练习
4.一个球与它的外切圆柱、外切等边圆锥(圆锥的轴截面为正三角形)的体积之比( )
A.2∶3∶5 B.2∶3∶4 C.3∶5∶8 D.4∶6∶9
例题7 已知R的球面上有A、B两点,它们的球面距离是 R,则线段AB的长为( )
A. B.
C. D.
练习
5.已知球面上两点A,B之间的球面距离为4π,过这两点的两条球半径之间的夹角为60°,以AB为直径的球的小圆的面积为_____________.
例题8 如图,三棱柱ABC—A'B'C'中,若E、F分别为AB、AC 的中点,平面EB'C'将三棱柱分成体积为V1、V2的两部分,那么V1:V2=_____ .
题型七 几何体的割补求体积问题
1.如图,将一个长方体用过相邻三条棱中点的平面截出一个棱锥,则该棱锥的体积与剩下的几何体的体积的比是______.
练习
例题9 如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现,圆柱的体积与球的体积之比为 ,圆柱的表面积与球的表面积之比为 .
题型八 数学史
1.木星的表面积约是地球的120倍,体积约是地球的____ __倍.
练习
2.我国古代数学名著《九章算术?商功》中将底面是直角三角形的直三棱柱称之为“堑堵”,如图为一个堑堵ABC﹣DFE,AB⊥BC,AB=6,其体积为120,若将该“堑堵”放入一个球形容器中,则该球形容器表面积的最小值为( )
A.100π B.108π
C.116π D.120π
谢谢!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
