第4章 三角形 A卷-2020-2021学年北师大版七年级数学下册单元测试AB卷(Word版 含答案)
文档属性
| 名称 | 第4章 三角形 A卷-2020-2021学年北师大版七年级数学下册单元测试AB卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 492.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-24 10:15:24 | ||
图片预览


文档简介
第4章
三角形A卷
考试时间:90分钟,总分:120
一、单选题(将唯一正确答案的代号填在题后括号内,每题3分,共30分)
1.下列长度的各组线段中可组成三角形的是(
)
A.1,2,3
B.2,5,8
C.6,2,2
D.3,5,3
2.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等腰三角形都全等
3.下列条件中不能判断两个三角形全等的是(
)
A.有两边和它们的夹角对应相等
B.有两边和其中一边的对角对应相等
C.有两角和它们的夹边对应相等
D.有两角和其中一角的对边对应相等
4.给出下列关于三角形的条件:①已知三边;②已知两边及其夹角;③已知两角及其夹边;④已知两边及其中一边的对角.利用尺规作图,能作出唯一的三角形的条件是(
)
A.①②③
B.①②④
C.②③④
D.①③④
5.下面四个图形中,线段BD是△ABC的高的图形是(
)
A.B.C.D.
6.如图,已知O是线段AC和BD的中点,要说明△ABO≌△CDO,以下回答最合理的是( )
A.添加条件∠A=∠C
B.添加条件AB=CD
C.不需要添加条件
D.△ABO和△CDO不可能全等
6题图
7题图
8题图
7.如图,已知△ABD≌△ACE,下列说法错误的是(
)
A.∠B=∠C
B.EB=DC
C.AD=DC
D.△EFB≌△DFC
8.如图,△ABC≌△ADE,BC的延长线交DA于F,交DE于G,∠D=25°,∠E=105°,∠DAC=16°,则∠DGB的度数为(
)
A.66°
B.56°
C.50°
D.45°
9.如图,AD是△ABC的中线,E,F分别是AD及AD延长线上的点,且DE=DF,连结BF,CE,下列说法:①CE=BF;②△ABD和△ACD面积相等:③BF∥CE;④∠BAD=∠CAD;其中正确的是(
)
A.1个
B.2个
C.3个
D.4个
9题图
10题图
10.如图,△ABC≌△ADE,点A、B、E在同一直线上,∠B=20°,∠BAD=60°,则∠C的度数为(
)
A.20°
B.30°
C.40°
D.60°
二、填空题(将正确答案填在题中横线上,每题3分,共24分)
11.一个三角形的两边长分别为2和5,若第三边取奇数,则此三角形的周长为_____.
12.如图,△ABC≌△ADE,如果AB=5cm,
BC=7cm,
AC=6cm,,那么DE的长是______.
12题图
13题图
14题图
13.如图,∠1=∠2,由SAS判定△ABD≌△ACD,则需添加的条件_____.
14.如图,在方格纸中,以AB为一边作△ABP,使△ABC与△ABP全等,P1,P2,P3,P4四个点中符合条件的点P的个数为_________.
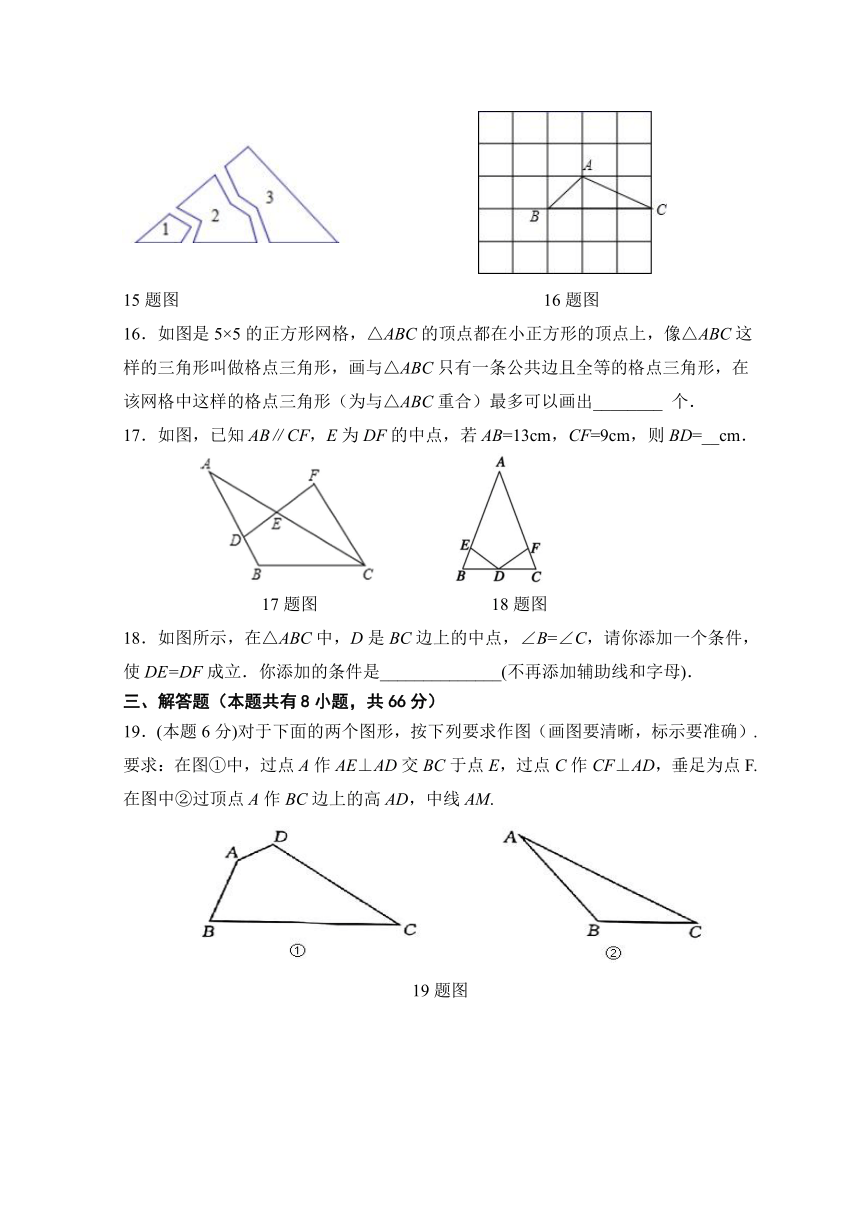
15.如图,某同学把三角形玻璃打碎三块,现在他要去配一块完全一样的,结果他带了第3片去,他所用到的原理是__________(用文字语言表述).
15题图
16题图
16.如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫做格点三角形,画与△ABC只有一条公共边且全等的格点三角形,在该网格中这样的格点三角形(为与△ABC重合)最多可以画出________
个.
17.如图,已知AB∥CF,E为DF的中点,若AB=13cm,CF=9cm,则BD=__cm.
17题图
18题图
18.如图所示,在△ABC中,D是BC边上的中点,∠B=∠C,请你添加一个条件,使DE=DF成立.你添加的条件是______________(不再添加辅助线和字母).
三、解答题(本题共有8小题,共66分)
19.(本题6分)对于下面的两个图形,按下列要求作图(画图要清晰,标示要准确).
要求:在图①中,过点A作AE⊥AD交BC于点E,过点C作CF⊥AD,垂足为点F.在图中②过顶点A作BC边上的高AD,中线AM.
19题图
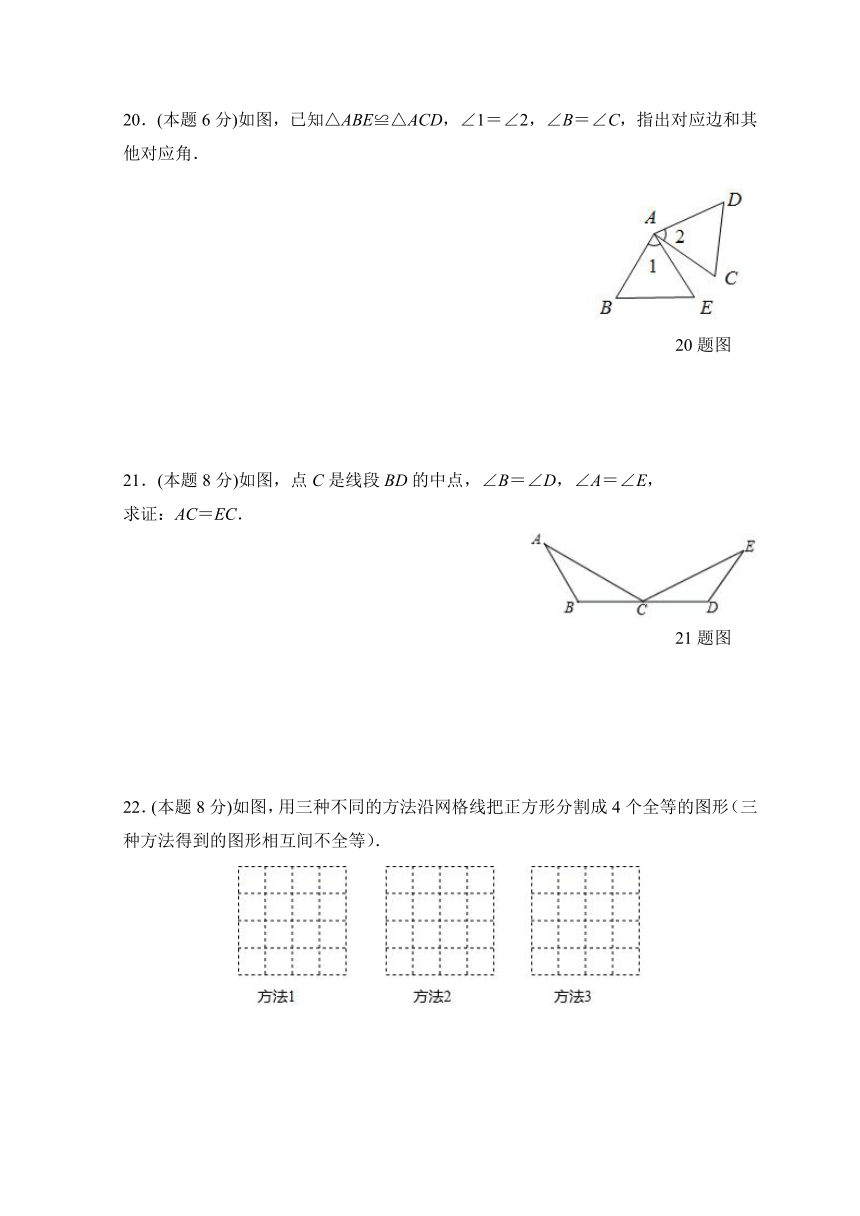
20.(本题6分)如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,指出对应边和其他对应角.
20题图
21.(本题8分)如图,点C是线段BD的中点,∠B=∠D,∠A=∠E,
求证:AC=EC.
21题图
22.(本题8分)如图,用三种不同的方法沿网格线把正方形分割成4个全等的图形(三种方法得到的图形相互间不全等).
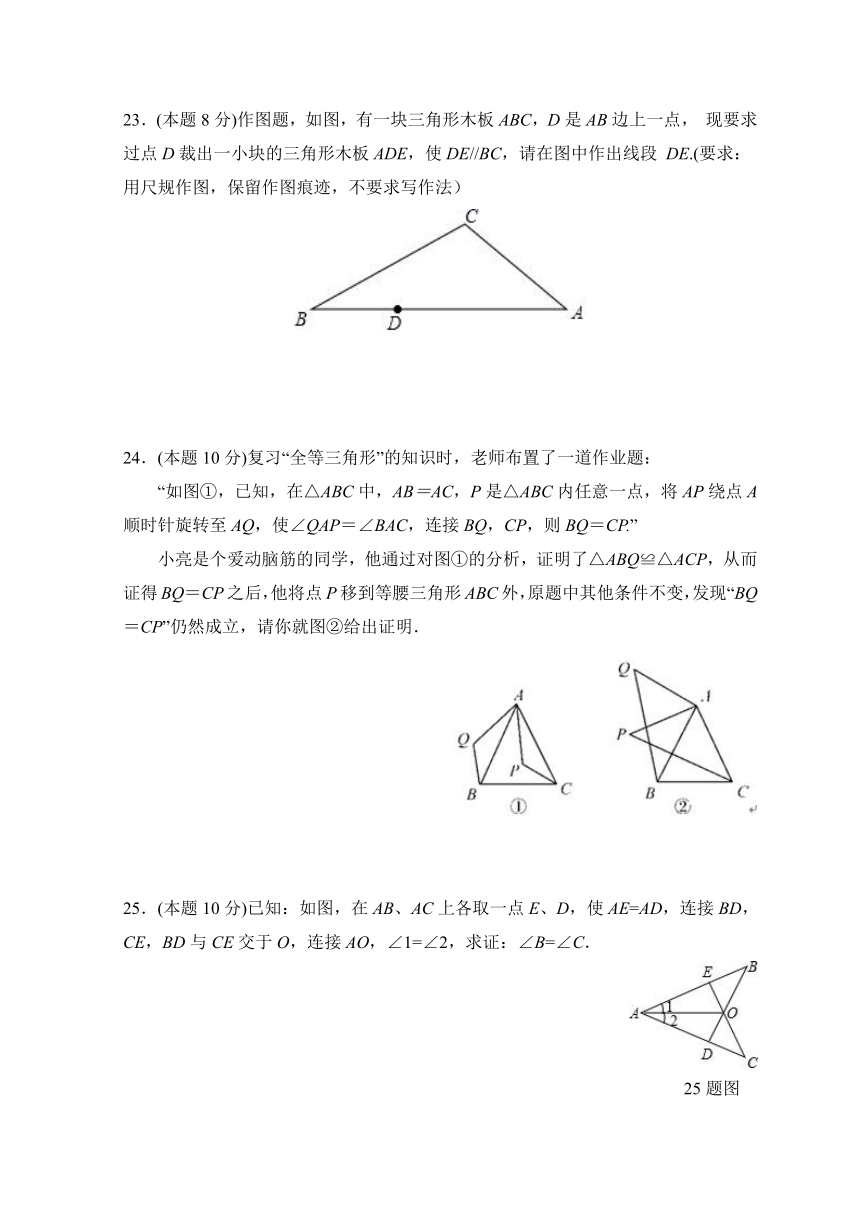
23.(本题8分)作图题,如图,有一块三角形木板ABC,D是AB边上一点,
现要求过点D裁出一小块的三角形木板ADE,使DE//BC,请在图中作出线段
DE.(要求:用尺规作图,保留作图痕迹,不要求写作法)
24.(本题10分)复习“全等三角形”的知识时,老师布置了一道作业题:
“如图①,已知,在△ABC中,AB=AC,P是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,则BQ=CP.”
小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP之后,他将点P移到等腰三角形ABC外,原题中其他条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
25.(本题10分)已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,求证:∠B=∠C.
25题图
26.(本题10分)(1)如图①,已知:△ABC中,,,直线m经过点A,于D,于E,求证:;
(2)拓展:如图②,将(1)中的条件改为:△ABC中,,D、A、E三点都在直线m上,并且,为任意锐角或钝角,请问结论是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图③,在△ABC中,是钝角,,,,直线m与BC的延长线交于点F,若,△ABC的面积是12,求△ABD与△CEF的面积之和.
第4章
三角形A卷参考答案
1.D.
解析:A选项:1+2=3,故不能构成三角形;
B选项:2+5=7<8,故不能构成三角形;
C选项:2+2=4<6,故不能构成三角形;
D选项:3+3=6>5,故能构成三角形;
故选:D.
2.C.
解析:A、形状相同的两个三角形全等,说法错误,本选项不符合题意;
B、面积相等的两个三角形全等,说法错误,本选项不符合题意;
C、完全重合的两个三角形全等,说法正确,本选项符合题意;
D、所有的等腰三角形都全等,说法错误,本选项不符合题意.
故选
:C.
3.B.
解析:∵全等三角形的判定定理有SAS,ASA,AAS,SSS,
∴A、符合SAS定理,即能推出两三角形全等,正确,故本选项错误;
B、不符合全等三角形的判定定理,即不能推出两三角形全等,错误,故本选项正确;
C、符合ASA定理,即能推出两三角形全等,正确,故本选项错误;
D、符合AAS定理,即能推出两三角形全等,正确,故本选项错误;
故选:B.
4.A.
解析:①是根据边边边(SSS);②是根据两边夹一角(SAS);③是根据两角夹一边(ASA)都成立.根据三角形全等的判定,都可以确定唯一的三角形;
而④则不能.
故选A.
5.D.
解析:根据所给图形判断,
如图中的BD是三角形的高.
故选:D.
6.C.
解析:∵O是线段AC和BD的中点,∴OA=OC,OB=OD,
又∵∠AOB=∠COD,∴△ABO≌△CDO(SAS)
故选:C.
7.C.
解析:∵△ABD≌△ACE,∴∠B=∠C,AB=AC,AE=AD,
∴AB-AE=AC-AD,∴BE=CD,
在△EFB和△DFC中
,
∴△EFB≌△DFC(AAS),无法证得AD=DC,
∴正确的说法是A、B、D,错误的说法是C.
故选:C.
8.A.
解析:,,,
,,,
解得,,
在中,,
,,
解得,
故选:A.
9.C.
解析:在△BDF和△CDE中,
,
∴△BDF≌△CDE(SAS),
∴CE=BF,∠F=∠DEC,∴BF∥CE,故①③正确;
∵BD=CD,点A到BD、CD的距离相等,
∴△ABD和△ACD面积相等,故②正确;
∵AD为△ABC的中线,
∴BD=CD,∠BAD和∠CAD不一定相等,故④错误;
综上,①②③正确,共3个,故选:C.
10.C.
解析:∵,∴,,
∴,
∴,
故选:C.
11.12.
解析:设第三边长为x.根据三角形的三边关系,则有5-2<x<5+2,
即3<x<7.所以x=5.所以周长=2+5+5=12.
故答案为:12.
12..
解析:,,
,,
故答案为:.
13.∠B=∠C或AB=AC.
解析:本题要判定△ABD≌△ACD,已知∠1=∠2,AD是公共边,具备了一边一角对应相等,再有AB=AC,就可以用SAS,
也可以使用“AAS”的条件;选∠B=∠C.
所以,填∠B=∠C或AB=AC.
14.3.
解析:要使△ABP与△ABC全等,点P到AB的距离应该等于点C到AB的距离,即3个单位长度,故点P的位置可以是P1,P2,P4三个,故答案为3.
15.两角及夹边对应相等的两个三角形全等.
解析:根据题意可知第3块保留了原三角形的两个角还保留了其中一个边,∴两角及夹边对应相等的两个三角形全等,故拿第3块去即可.
故答案为:两角及夹边对应相等的两个三角形全等
16.6.
解析:
以BC为公共边可以画出△BDC,
△BEC,△BFC三个三角形和原三角形全等;
以AB为公共边可以画出△ABG,
△ABM,△ABH三个三角形和原三角形全等;
所以可以画出6个
故答案为:6.
17.4.
解析:∵AB∥CF,∴∠ADE=∠EFC,
∵∠AED=∠FEC,E为DF的中点,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(ASA),
∴AD=CF=9cm,
∵AB=13cm,∴BD=13-9=4(cm).
故答案为:4.
18.BE=CF(答案不唯一).
解析:添加条件是BE=CF,
∵D是BC边上的中点,
∴BD=CD,
在△BED和△CFD中
∴
∴,
故答案:BE=CF(答案不唯一).
19.解:作图如图①②所示.
20.解:∵△ABE≌△ACD,∠1=∠2,∠B=∠C,
∴点A的对应点是A,点B的对应点是C,点E的对应点是D,
∴∠E与∠D是对应角,
AB与AC,BE与CD,AE与AD是对应边.
21.解:∵点C是线段BD的中点,∴BC=CD,
在△ABC和△EDC中,
,
∴△ABC≌△EDC(AAS),
∴AC=EC.
22.解:如图所示:
.
23.解:要使DE//BC,可在D点作BC的平行线即可,即可作∠EDA=∠CBA,先以B为圆心画弧,交BA,BC边两点,再以D为圆心相同半径画弧,然后以B为圆心的弧与边的其中一交点为圆心,到另一交点长度为半径画弧,再以相同半径以刚D为圆心的弧与BA交点为圆心画弧,连接D和两弧交点与CA相交及为点E.
24.证明:∵∠QAP=∠BAC,
∴∠QAP+∠PAB=∠PAB+∠BAC,即∠QAB=∠PAC,
在△ABQ和△ACP中:,
∴△ABQ≌△ACP,
∴BQ=CP.
25.证明:在和中,
,,
,
由对顶角相等得:,
,即,
在和中,
,,
.
26.(1)证明:直线m,直线m,
,
,,
,,
在和中,,
≌,
,,
;
(2)解:结论成立;理由如下:
,
,
,
在和中,,
≌,
,,
;
(3)解:,,
,
在和中,,
≌,
,
设的底边BC上的高为h,则的底边CF上的高为h,
,,
,,
,
与的面积之和为6.
三角形A卷
考试时间:90分钟,总分:120
一、单选题(将唯一正确答案的代号填在题后括号内,每题3分,共30分)
1.下列长度的各组线段中可组成三角形的是(
)
A.1,2,3
B.2,5,8
C.6,2,2
D.3,5,3
2.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等腰三角形都全等
3.下列条件中不能判断两个三角形全等的是(
)
A.有两边和它们的夹角对应相等
B.有两边和其中一边的对角对应相等
C.有两角和它们的夹边对应相等
D.有两角和其中一角的对边对应相等
4.给出下列关于三角形的条件:①已知三边;②已知两边及其夹角;③已知两角及其夹边;④已知两边及其中一边的对角.利用尺规作图,能作出唯一的三角形的条件是(
)
A.①②③
B.①②④
C.②③④
D.①③④
5.下面四个图形中,线段BD是△ABC的高的图形是(
)
A.B.C.D.
6.如图,已知O是线段AC和BD的中点,要说明△ABO≌△CDO,以下回答最合理的是( )
A.添加条件∠A=∠C
B.添加条件AB=CD
C.不需要添加条件
D.△ABO和△CDO不可能全等
6题图
7题图
8题图
7.如图,已知△ABD≌△ACE,下列说法错误的是(
)
A.∠B=∠C
B.EB=DC
C.AD=DC
D.△EFB≌△DFC
8.如图,△ABC≌△ADE,BC的延长线交DA于F,交DE于G,∠D=25°,∠E=105°,∠DAC=16°,则∠DGB的度数为(
)
A.66°
B.56°
C.50°
D.45°
9.如图,AD是△ABC的中线,E,F分别是AD及AD延长线上的点,且DE=DF,连结BF,CE,下列说法:①CE=BF;②△ABD和△ACD面积相等:③BF∥CE;④∠BAD=∠CAD;其中正确的是(
)
A.1个
B.2个
C.3个
D.4个
9题图
10题图
10.如图,△ABC≌△ADE,点A、B、E在同一直线上,∠B=20°,∠BAD=60°,则∠C的度数为(
)
A.20°
B.30°
C.40°
D.60°
二、填空题(将正确答案填在题中横线上,每题3分,共24分)
11.一个三角形的两边长分别为2和5,若第三边取奇数,则此三角形的周长为_____.
12.如图,△ABC≌△ADE,如果AB=5cm,
BC=7cm,
AC=6cm,,那么DE的长是______.
12题图
13题图
14题图
13.如图,∠1=∠2,由SAS判定△ABD≌△ACD,则需添加的条件_____.
14.如图,在方格纸中,以AB为一边作△ABP,使△ABC与△ABP全等,P1,P2,P3,P4四个点中符合条件的点P的个数为_________.
15.如图,某同学把三角形玻璃打碎三块,现在他要去配一块完全一样的,结果他带了第3片去,他所用到的原理是__________(用文字语言表述).
15题图
16题图
16.如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫做格点三角形,画与△ABC只有一条公共边且全等的格点三角形,在该网格中这样的格点三角形(为与△ABC重合)最多可以画出________
个.
17.如图,已知AB∥CF,E为DF的中点,若AB=13cm,CF=9cm,则BD=__cm.
17题图
18题图
18.如图所示,在△ABC中,D是BC边上的中点,∠B=∠C,请你添加一个条件,使DE=DF成立.你添加的条件是______________(不再添加辅助线和字母).
三、解答题(本题共有8小题,共66分)
19.(本题6分)对于下面的两个图形,按下列要求作图(画图要清晰,标示要准确).
要求:在图①中,过点A作AE⊥AD交BC于点E,过点C作CF⊥AD,垂足为点F.在图中②过顶点A作BC边上的高AD,中线AM.
19题图
20.(本题6分)如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,指出对应边和其他对应角.
20题图
21.(本题8分)如图,点C是线段BD的中点,∠B=∠D,∠A=∠E,
求证:AC=EC.
21题图
22.(本题8分)如图,用三种不同的方法沿网格线把正方形分割成4个全等的图形(三种方法得到的图形相互间不全等).
23.(本题8分)作图题,如图,有一块三角形木板ABC,D是AB边上一点,
现要求过点D裁出一小块的三角形木板ADE,使DE//BC,请在图中作出线段
DE.(要求:用尺规作图,保留作图痕迹,不要求写作法)
24.(本题10分)复习“全等三角形”的知识时,老师布置了一道作业题:
“如图①,已知,在△ABC中,AB=AC,P是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,则BQ=CP.”
小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP之后,他将点P移到等腰三角形ABC外,原题中其他条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
25.(本题10分)已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,求证:∠B=∠C.
25题图
26.(本题10分)(1)如图①,已知:△ABC中,,,直线m经过点A,于D,于E,求证:;
(2)拓展:如图②,将(1)中的条件改为:△ABC中,,D、A、E三点都在直线m上,并且,为任意锐角或钝角,请问结论是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图③,在△ABC中,是钝角,,,,直线m与BC的延长线交于点F,若,△ABC的面积是12,求△ABD与△CEF的面积之和.
第4章
三角形A卷参考答案
1.D.
解析:A选项:1+2=3,故不能构成三角形;
B选项:2+5=7<8,故不能构成三角形;
C选项:2+2=4<6,故不能构成三角形;
D选项:3+3=6>5,故能构成三角形;
故选:D.
2.C.
解析:A、形状相同的两个三角形全等,说法错误,本选项不符合题意;
B、面积相等的两个三角形全等,说法错误,本选项不符合题意;
C、完全重合的两个三角形全等,说法正确,本选项符合题意;
D、所有的等腰三角形都全等,说法错误,本选项不符合题意.
故选
:C.
3.B.
解析:∵全等三角形的判定定理有SAS,ASA,AAS,SSS,
∴A、符合SAS定理,即能推出两三角形全等,正确,故本选项错误;
B、不符合全等三角形的判定定理,即不能推出两三角形全等,错误,故本选项正确;
C、符合ASA定理,即能推出两三角形全等,正确,故本选项错误;
D、符合AAS定理,即能推出两三角形全等,正确,故本选项错误;
故选:B.
4.A.
解析:①是根据边边边(SSS);②是根据两边夹一角(SAS);③是根据两角夹一边(ASA)都成立.根据三角形全等的判定,都可以确定唯一的三角形;
而④则不能.
故选A.
5.D.
解析:根据所给图形判断,
如图中的BD是三角形的高.
故选:D.
6.C.
解析:∵O是线段AC和BD的中点,∴OA=OC,OB=OD,
又∵∠AOB=∠COD,∴△ABO≌△CDO(SAS)
故选:C.
7.C.
解析:∵△ABD≌△ACE,∴∠B=∠C,AB=AC,AE=AD,
∴AB-AE=AC-AD,∴BE=CD,
在△EFB和△DFC中
,
∴△EFB≌△DFC(AAS),无法证得AD=DC,
∴正确的说法是A、B、D,错误的说法是C.
故选:C.
8.A.
解析:,,,
,,,
解得,,
在中,,
,,
解得,
故选:A.
9.C.
解析:在△BDF和△CDE中,
,
∴△BDF≌△CDE(SAS),
∴CE=BF,∠F=∠DEC,∴BF∥CE,故①③正确;
∵BD=CD,点A到BD、CD的距离相等,
∴△ABD和△ACD面积相等,故②正确;
∵AD为△ABC的中线,
∴BD=CD,∠BAD和∠CAD不一定相等,故④错误;
综上,①②③正确,共3个,故选:C.
10.C.
解析:∵,∴,,
∴,
∴,
故选:C.
11.12.
解析:设第三边长为x.根据三角形的三边关系,则有5-2<x<5+2,
即3<x<7.所以x=5.所以周长=2+5+5=12.
故答案为:12.
12..
解析:,,
,,
故答案为:.
13.∠B=∠C或AB=AC.
解析:本题要判定△ABD≌△ACD,已知∠1=∠2,AD是公共边,具备了一边一角对应相等,再有AB=AC,就可以用SAS,
也可以使用“AAS”的条件;选∠B=∠C.
所以,填∠B=∠C或AB=AC.
14.3.
解析:要使△ABP与△ABC全等,点P到AB的距离应该等于点C到AB的距离,即3个单位长度,故点P的位置可以是P1,P2,P4三个,故答案为3.
15.两角及夹边对应相等的两个三角形全等.
解析:根据题意可知第3块保留了原三角形的两个角还保留了其中一个边,∴两角及夹边对应相等的两个三角形全等,故拿第3块去即可.
故答案为:两角及夹边对应相等的两个三角形全等
16.6.
解析:
以BC为公共边可以画出△BDC,
△BEC,△BFC三个三角形和原三角形全等;
以AB为公共边可以画出△ABG,
△ABM,△ABH三个三角形和原三角形全等;
所以可以画出6个
故答案为:6.
17.4.
解析:∵AB∥CF,∴∠ADE=∠EFC,
∵∠AED=∠FEC,E为DF的中点,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(ASA),
∴AD=CF=9cm,
∵AB=13cm,∴BD=13-9=4(cm).
故答案为:4.
18.BE=CF(答案不唯一).
解析:添加条件是BE=CF,
∵D是BC边上的中点,
∴BD=CD,
在△BED和△CFD中
∴
∴,
故答案:BE=CF(答案不唯一).
19.解:作图如图①②所示.
20.解:∵△ABE≌△ACD,∠1=∠2,∠B=∠C,
∴点A的对应点是A,点B的对应点是C,点E的对应点是D,
∴∠E与∠D是对应角,
AB与AC,BE与CD,AE与AD是对应边.
21.解:∵点C是线段BD的中点,∴BC=CD,
在△ABC和△EDC中,
,
∴△ABC≌△EDC(AAS),
∴AC=EC.
22.解:如图所示:
.
23.解:要使DE//BC,可在D点作BC的平行线即可,即可作∠EDA=∠CBA,先以B为圆心画弧,交BA,BC边两点,再以D为圆心相同半径画弧,然后以B为圆心的弧与边的其中一交点为圆心,到另一交点长度为半径画弧,再以相同半径以刚D为圆心的弧与BA交点为圆心画弧,连接D和两弧交点与CA相交及为点E.
24.证明:∵∠QAP=∠BAC,
∴∠QAP+∠PAB=∠PAB+∠BAC,即∠QAB=∠PAC,
在△ABQ和△ACP中:,
∴△ABQ≌△ACP,
∴BQ=CP.
25.证明:在和中,
,,
,
由对顶角相等得:,
,即,
在和中,
,,
.
26.(1)证明:直线m,直线m,
,
,,
,,
在和中,,
≌,
,,
;
(2)解:结论成立;理由如下:
,
,
,
在和中,,
≌,
,,
;
(3)解:,,
,
在和中,,
≌,
,
设的底边BC上的高为h,则的底边CF上的高为h,
,,
,,
,
与的面积之和为6.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
