第5章 生活中的轴对称 B卷-2020-2021学年北师大版七年级数学下册单元测试AB卷(Word版 含答案)
文档属性
| 名称 | 第5章 生活中的轴对称 B卷-2020-2021学年北师大版七年级数学下册单元测试AB卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-24 10:22:01 | ||
图片预览




文档简介
第5章
生活中的轴对称B卷
考试时间:90分钟,总分:120
一、单选题(将唯一正确答案的代号填在题后括号内,每题3分,共30分)
1.下列标志中,可以看作是轴对称图形的是(
)
A.
B.
C.
D.
2.下列图形中,不是轴对称图形的是(
)
A.
B.
C.
D.
3.下列图形中,不是轴对称图形的是(
)
A.有两个内角相等的三角形
B.有一个内角是45°直角三角形
C.有一个内角是30°的直角三角形
D.有两个角分别是30°和120°的三角形
4.有以下几何图形:①线段;②角;③等腰三角形;④直角三角形;⑤梯形;⑥平行四边形,其中一定是轴对称图形的有(
)
A.1个
B.2个
C.3个
D.4个
5.下列图形不是轴对称图形的是( )
A.
B.
C.
D.
6.下面是四位同学所作的△ABC关于直线MN对称的图形,其中正确的是(
)
A.B.
C.
D.
7.如图,已知长方形纸片ABCD,点E,H在AD边上,点F,G在BC边上,分别沿EF,GH折叠,使点B和点C都落在点P处,若∠FEH+∠EHG=118°,则∠FPG的度数为( )
A.54°
B.55°
C.56°
D.57°
7题图
8题图
8.如图,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为(
)
A.
B.
C.
D.
9.如图,在4×4的正方形网格中,有A,B两点,在直线a上求一点P,使PA+PB最短,则点P的位置应选在(
)
A.C点
B.D点
C.E点
D.F点
9题图
10题图
10.如图,在△ABE中,∠BAE=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )
A.45°
B.60°
C.50°
D.55°
二、填空题(将正确答案填在题中横线上,每题3分,共24分)
11.角是轴对称图形,它的对称轴是
.
12.在“线段、圆、等边三角形、正方形、角”这五个图形中,对称轴最多的图形是______.
13.如图,∠A=100°,∠E=25°,△ABC与△DEF关于直线对称,则∠C=_____.
13题图
14题图
14.如图,在△ABC中,点D为BC边上一点,点D关于AB,AC对称的点分别为E、F,连接EF分别交AB、AC于M、N,分别连接DM、DN,已知△DMN的周长是6cm,那么EF=___________.
15.如图的三角形纸片中,AB=6,AC=7,BC=5,沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则△AED的周长为______.
15题图
16题图
16.如图,△ABC中三边长分别为a
、b
、c满足a
10,b
8,c
14.若沿过C的直线折叠,使点A落在BC边上的点E处,折痕为CD
,则DEB的周长为
.
17.如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C、D落在AB边上的C'、D'处,折痕为MN,则∠AMD'+∠BNC'=
.?
17题图
18题图
18.如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠α的度数为
度.
三、解答题(本题共有8小题,共66分)
19.(本题8分)已知等腰三角形的一边等于4,另一边等于9,求它的周长.
20.(本题8分)两个大小不同的圆在同平面内可以组成下图的五组图形,请画出每组图形的对称轴,并说一说它们的对称轴有什么共同的特点.
21.(本题8分)请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知:如图△ABC.
求作:一点,使点到边与距离相等,且点到点与点的距离也相等.
21题图
22.(本题8分)如图,将长方形纸条ABCD沿EF,GH同时折叠,B,C两点恰好都落在AD边的点P处,若△PFH的周长为10cm,AB=2cm,求长方形ABCD的面积.
22题图
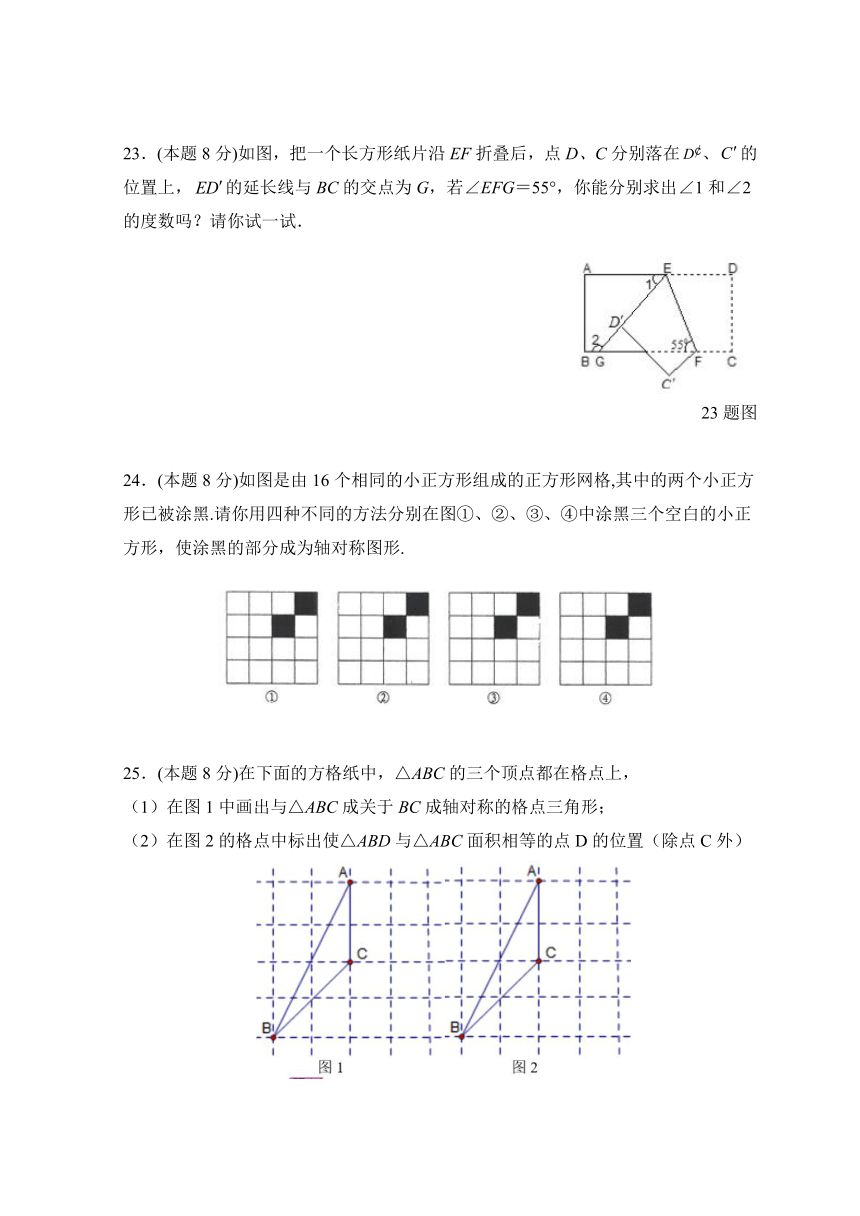
23.(本题8分)如图,把一个长方形纸片沿EF折叠后,点D、C分别落在、的位置上,的延长线与BC的交点为G,若∠EFG=55°,你能分别求出∠1和∠2的度数吗?请你试一试.
23题图
24.(本题8分)如图是由16个相同的小正方形组成的正方形网格,其中的两个小正方形已被涂黑.请你用四种不同的方法分别在图①、②、③、④中涂黑三个空白的小正方形,使涂黑的部分成为轴对称图形.
25.(本题8分)在下面的方格纸中,△ABC的三个顶点都在格点上,
(1)在图1中画出与△ABC成关于BC成轴对称的格点三角形;
(2)在图2的格点中标出使△ABD与△ABC面积相等的点D的位置(除点C外)
26.(本题10分)问题提出:如图,在四边形ABCD中,∠BAD=α,∠BCD=180°-α,BD平分∠ABC.
(1)如图1,若α=90°,根据教材中一个重要性质直接可得DA=CD,这个性质是角平分线上的点到这个角的两边的距离相等;
(2)问题解决:如图2,求证AD=CD;
(3)问题拓展:如图3,在等腰三角形ABC中,∠BAC=100°,BD平分∠ABC,求证:BD+AD=BC.
第5章
生活中的轴对称B卷参考答案
1.
C.
解析:根据轴对称的概念对各小题分析判断即可得选项C是轴对称图形.
故选C.
2.D.
解析:A、是轴对称图形,故本选项不符合题意;
B、是轴对称图形,故本选项不符合题意;
C、是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项符合题意.
故选:D.
3.C.
解析:因为有两个内角相等的三角形是等腰三角形,是轴对称图形,所以A正确;
因为有一个内角是45°直角三角形是等腰直角三角形,是轴对称图形,所以B正确;
因为有一个内角是30°的直角三角形,不是轴对称图形,所以C错误;
因为有两个角分别是30°和120°的三角形是等腰三角形,是轴对称图形,所以D正确,
故选C.
4.C.
解析:其中一定是轴对称图形的有①线段;②角;③等腰三角形;
故答案为:C.
5.C.
解析:A.是轴对称图形,故本选项错误;
B.是轴对称图形,故本选项错误;
C.不是轴对称图形,故本选项正确;
D.是轴对称图形,故本选项错误.
故选:C
6.D.
解析:A:对称点连接的直线与对称轴不垂直,故选项A错误;
B:对称点不在对称轴上,故选项B错误;
C:对称点连接的直线到对称轴的距离不相等,故选项C错误;
故答案选择:D.
7.C.
解析:∵四边形ABCD是长方形,∴AD∥BC,
∴∠FEH=∠BFE,∠EHG=∠CGH,
∴∠BFE+∠CGH=∠FEH+∠EHG=118°,
由折叠可知:EF,GH分别是∠BFP和∠CGP的角平分线,
∴∠PFE=∠BFE,∠PGH=∠CGH,
∴∠PFE+∠PGH=∠BFE+∠CGH=118°,
∴∠BFP+∠CGP=2(∠BFE+∠CGH)=236°,
∴∠PFG+∠PGF=360°﹣(∠BFP+∠CGP)=360°﹣236°=124°,
∴∠FPG=180°﹣(∠PFG+∠PGF)=180°﹣124°=56°.
故选:C.
8.C.
解析:要使白球反弹后能将黑球直接撞入袋中,必须∠2+∠3=90°,
∵∠3=30°,∴∠2=60°。∴根据入射角等于反射角,得∠1=∠2=60°。故选C。
9.A.
解析:如图,
点是点A关于直线a的对称点,连接,则与直线a的交点即为点P,此时最短.
∵与直线a交于点C,∴点P的位置应选在C点.故选:A.
10.C.
解析:∵MN是AE的垂直平分线,∴AC=EC,
∴∠CAE=∠E,∴∠ACB=∠CAE+∠E=2∠E,
∵AB=CE,∴∠B=∠ACB=2∠E,
在△ABC中,∠BAE+∠B+∠E=180°,
∴105°+2∠E+∠E=180°,即∠E=25°.
∴∠B=2∠E=50°.
故选C.
11.角平分线所在的直线.
解析:角是轴对称图形,它的对称轴是:角的平分线所在直线.
12.圆.
解析:线段有2条对称轴;圆有无数条对称轴;等边三角形有3条对称轴;
正方形有4条对称轴;角有1条对称轴;故答案为圆.
13.55.
解析:∵∠A=100°,∠E=25°,△ABC与△DEF关于直线l对称,
∴∠B=∠E=25°,∴∠C=180°?∠A?∠B=55°,故答案为:55.
14.6
cm.
解析:由轴对称的性质知,EM=DM,FN=DN,
∴EF=EM+MN+FN=DM+MN+DN=△DMN的周长=6cm.
∴△DMN的周长=EF=6
cm.故答案是:6
cm.
15.8.
解析:折叠后EB=BC,ED=DC,所以周长=AD+DE+AE=AC+AB–BC=8.
16.16.
解析:由题意可知:△ADC≌△EDC,
∴AC=CE=8,AD=DE,∴BE=BC?CE=10?8=2,
∴△DEB的周长为:DB+DE+BE=DB+AD+BE=AB+BE=14+2=16,
故答案为:16
17.60°.
解析:四边形纸片ABCD中,∠A=70°,∠B=80°,
∴∠D+∠C=360°-∠A-∠B=210°,
∵将纸片折叠,使C,D落在AB边上的C',D'处,
∴∠MD'B=∠D,∠NC'A=∠C,
∴∠MD'B+∠NC'A=210°,
∴∠AD'M+∠BC'N=150°,
∴∠AMD'+∠BNC'=360°-∠A-∠B-∠AD'M-∠BC'N=60°.
18.80.
解析:设∠3=3x,则∠1=28x,∠2=5x,
∵∠1+∠2+∠3=180°,∴28x+5x+3x=180°,解得x=5°,
∴∠1=140°,∠2=25°,∠3=15°,
∵△ABE是△ABC沿着AB边翻折180°形成的,
∴∠1=∠BAE=140°,∠E=∠3=15°,
∴∠EAC=360°-∠BAE-∠BAC=360°-140°-140°=80°,
又∵△ADC是△ABC沿着AC边翻折180°形成的,
∴∠ACD=∠E=15°,而∠α+∠E=∠EAC+∠ACD,
∴∠α=∠EAC=80°.故答案为80°.
19.解:当4为腰,9为底时,∵4+4<9,∴不能构成三角形;
当腰为9时,∵9+9>4,∴能构成三角形,
∴等腰三角形的周长为:9+9+4=22.
20.解:如图所示:
共同特点:它们的对称轴均为经过两圆圆心的一条直线.
21.解:如图所示,点O为所求作的点.
22.解:将长方形ABCD沿EF,GH同时折叠,B、C两点恰好都落在AD边的P点处,
,,
的周长为,,
.
又,∴长方形ABCD的面积为:.
23.解:,,
由翻折的性质,得
.
24.解:如下图,
25.(1)如图,△A′BC就是所求的图形.
(2)如图:D1、D2、D3、D4就是所求的点.
26.
解:(2)证明:如图1,作DE⊥BA交BA延长线于E,DF⊥BC于F.
∵BD平分∠EBF,DE⊥BE,DF⊥BF,∴DE=DF,
∵∠BAD+∠C=180°,∠BAD+∠EAD=180°,∴∠DAE=∠C,
在△DEA和△DFC中,
∴△DEA≌△DFC(AAS),∴AD=CD.
(3)证明:如图2,在BC时截取BK=BD,连接DK,
∵AB=AC,∠BAC=100°,∴∠ABC=∠C=40°.
∵BD平分∠ABC,∴∠DBK=∠ABC=20°.
∵BD=BK,∴∠BKD=∠BDK=80°,即∠A+∠BKD=180°,
由(2)的结论得AD=DK,
∵∠BKD=180°-∠DKC=∠C+∠KDC,
∴∠KDC=∠C=40°,∴DK=CK,
∴AD=DK=CK,∴BD+AD=BK+CK=BC.
生活中的轴对称B卷
考试时间:90分钟,总分:120
一、单选题(将唯一正确答案的代号填在题后括号内,每题3分,共30分)
1.下列标志中,可以看作是轴对称图形的是(
)
A.
B.
C.
D.
2.下列图形中,不是轴对称图形的是(
)
A.
B.
C.
D.
3.下列图形中,不是轴对称图形的是(
)
A.有两个内角相等的三角形
B.有一个内角是45°直角三角形
C.有一个内角是30°的直角三角形
D.有两个角分别是30°和120°的三角形
4.有以下几何图形:①线段;②角;③等腰三角形;④直角三角形;⑤梯形;⑥平行四边形,其中一定是轴对称图形的有(
)
A.1个
B.2个
C.3个
D.4个
5.下列图形不是轴对称图形的是( )
A.
B.
C.
D.
6.下面是四位同学所作的△ABC关于直线MN对称的图形,其中正确的是(
)
A.B.
C.
D.
7.如图,已知长方形纸片ABCD,点E,H在AD边上,点F,G在BC边上,分别沿EF,GH折叠,使点B和点C都落在点P处,若∠FEH+∠EHG=118°,则∠FPG的度数为( )
A.54°
B.55°
C.56°
D.57°
7题图
8题图
8.如图,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为(
)
A.
B.
C.
D.
9.如图,在4×4的正方形网格中,有A,B两点,在直线a上求一点P,使PA+PB最短,则点P的位置应选在(
)
A.C点
B.D点
C.E点
D.F点
9题图
10题图
10.如图,在△ABE中,∠BAE=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )
A.45°
B.60°
C.50°
D.55°
二、填空题(将正确答案填在题中横线上,每题3分,共24分)
11.角是轴对称图形,它的对称轴是
.
12.在“线段、圆、等边三角形、正方形、角”这五个图形中,对称轴最多的图形是______.
13.如图,∠A=100°,∠E=25°,△ABC与△DEF关于直线对称,则∠C=_____.
13题图
14题图
14.如图,在△ABC中,点D为BC边上一点,点D关于AB,AC对称的点分别为E、F,连接EF分别交AB、AC于M、N,分别连接DM、DN,已知△DMN的周长是6cm,那么EF=___________.
15.如图的三角形纸片中,AB=6,AC=7,BC=5,沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则△AED的周长为______.
15题图
16题图
16.如图,△ABC中三边长分别为a
、b
、c满足a
10,b
8,c
14.若沿过C的直线折叠,使点A落在BC边上的点E处,折痕为CD
,则DEB的周长为
.
17.如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C、D落在AB边上的C'、D'处,折痕为MN,则∠AMD'+∠BNC'=
.?
17题图
18题图
18.如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠α的度数为
度.
三、解答题(本题共有8小题,共66分)
19.(本题8分)已知等腰三角形的一边等于4,另一边等于9,求它的周长.
20.(本题8分)两个大小不同的圆在同平面内可以组成下图的五组图形,请画出每组图形的对称轴,并说一说它们的对称轴有什么共同的特点.
21.(本题8分)请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知:如图△ABC.
求作:一点,使点到边与距离相等,且点到点与点的距离也相等.
21题图
22.(本题8分)如图,将长方形纸条ABCD沿EF,GH同时折叠,B,C两点恰好都落在AD边的点P处,若△PFH的周长为10cm,AB=2cm,求长方形ABCD的面积.
22题图
23.(本题8分)如图,把一个长方形纸片沿EF折叠后,点D、C分别落在、的位置上,的延长线与BC的交点为G,若∠EFG=55°,你能分别求出∠1和∠2的度数吗?请你试一试.
23题图
24.(本题8分)如图是由16个相同的小正方形组成的正方形网格,其中的两个小正方形已被涂黑.请你用四种不同的方法分别在图①、②、③、④中涂黑三个空白的小正方形,使涂黑的部分成为轴对称图形.
25.(本题8分)在下面的方格纸中,△ABC的三个顶点都在格点上,
(1)在图1中画出与△ABC成关于BC成轴对称的格点三角形;
(2)在图2的格点中标出使△ABD与△ABC面积相等的点D的位置(除点C外)
26.(本题10分)问题提出:如图,在四边形ABCD中,∠BAD=α,∠BCD=180°-α,BD平分∠ABC.
(1)如图1,若α=90°,根据教材中一个重要性质直接可得DA=CD,这个性质是角平分线上的点到这个角的两边的距离相等;
(2)问题解决:如图2,求证AD=CD;
(3)问题拓展:如图3,在等腰三角形ABC中,∠BAC=100°,BD平分∠ABC,求证:BD+AD=BC.
第5章
生活中的轴对称B卷参考答案
1.
C.
解析:根据轴对称的概念对各小题分析判断即可得选项C是轴对称图形.
故选C.
2.D.
解析:A、是轴对称图形,故本选项不符合题意;
B、是轴对称图形,故本选项不符合题意;
C、是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项符合题意.
故选:D.
3.C.
解析:因为有两个内角相等的三角形是等腰三角形,是轴对称图形,所以A正确;
因为有一个内角是45°直角三角形是等腰直角三角形,是轴对称图形,所以B正确;
因为有一个内角是30°的直角三角形,不是轴对称图形,所以C错误;
因为有两个角分别是30°和120°的三角形是等腰三角形,是轴对称图形,所以D正确,
故选C.
4.C.
解析:其中一定是轴对称图形的有①线段;②角;③等腰三角形;
故答案为:C.
5.C.
解析:A.是轴对称图形,故本选项错误;
B.是轴对称图形,故本选项错误;
C.不是轴对称图形,故本选项正确;
D.是轴对称图形,故本选项错误.
故选:C
6.D.
解析:A:对称点连接的直线与对称轴不垂直,故选项A错误;
B:对称点不在对称轴上,故选项B错误;
C:对称点连接的直线到对称轴的距离不相等,故选项C错误;
故答案选择:D.
7.C.
解析:∵四边形ABCD是长方形,∴AD∥BC,
∴∠FEH=∠BFE,∠EHG=∠CGH,
∴∠BFE+∠CGH=∠FEH+∠EHG=118°,
由折叠可知:EF,GH分别是∠BFP和∠CGP的角平分线,
∴∠PFE=∠BFE,∠PGH=∠CGH,
∴∠PFE+∠PGH=∠BFE+∠CGH=118°,
∴∠BFP+∠CGP=2(∠BFE+∠CGH)=236°,
∴∠PFG+∠PGF=360°﹣(∠BFP+∠CGP)=360°﹣236°=124°,
∴∠FPG=180°﹣(∠PFG+∠PGF)=180°﹣124°=56°.
故选:C.
8.C.
解析:要使白球反弹后能将黑球直接撞入袋中,必须∠2+∠3=90°,
∵∠3=30°,∴∠2=60°。∴根据入射角等于反射角,得∠1=∠2=60°。故选C。
9.A.
解析:如图,
点是点A关于直线a的对称点,连接,则与直线a的交点即为点P,此时最短.
∵与直线a交于点C,∴点P的位置应选在C点.故选:A.
10.C.
解析:∵MN是AE的垂直平分线,∴AC=EC,
∴∠CAE=∠E,∴∠ACB=∠CAE+∠E=2∠E,
∵AB=CE,∴∠B=∠ACB=2∠E,
在△ABC中,∠BAE+∠B+∠E=180°,
∴105°+2∠E+∠E=180°,即∠E=25°.
∴∠B=2∠E=50°.
故选C.
11.角平分线所在的直线.
解析:角是轴对称图形,它的对称轴是:角的平分线所在直线.
12.圆.
解析:线段有2条对称轴;圆有无数条对称轴;等边三角形有3条对称轴;
正方形有4条对称轴;角有1条对称轴;故答案为圆.
13.55.
解析:∵∠A=100°,∠E=25°,△ABC与△DEF关于直线l对称,
∴∠B=∠E=25°,∴∠C=180°?∠A?∠B=55°,故答案为:55.
14.6
cm.
解析:由轴对称的性质知,EM=DM,FN=DN,
∴EF=EM+MN+FN=DM+MN+DN=△DMN的周长=6cm.
∴△DMN的周长=EF=6
cm.故答案是:6
cm.
15.8.
解析:折叠后EB=BC,ED=DC,所以周长=AD+DE+AE=AC+AB–BC=8.
16.16.
解析:由题意可知:△ADC≌△EDC,
∴AC=CE=8,AD=DE,∴BE=BC?CE=10?8=2,
∴△DEB的周长为:DB+DE+BE=DB+AD+BE=AB+BE=14+2=16,
故答案为:16
17.60°.
解析:四边形纸片ABCD中,∠A=70°,∠B=80°,
∴∠D+∠C=360°-∠A-∠B=210°,
∵将纸片折叠,使C,D落在AB边上的C',D'处,
∴∠MD'B=∠D,∠NC'A=∠C,
∴∠MD'B+∠NC'A=210°,
∴∠AD'M+∠BC'N=150°,
∴∠AMD'+∠BNC'=360°-∠A-∠B-∠AD'M-∠BC'N=60°.
18.80.
解析:设∠3=3x,则∠1=28x,∠2=5x,
∵∠1+∠2+∠3=180°,∴28x+5x+3x=180°,解得x=5°,
∴∠1=140°,∠2=25°,∠3=15°,
∵△ABE是△ABC沿着AB边翻折180°形成的,
∴∠1=∠BAE=140°,∠E=∠3=15°,
∴∠EAC=360°-∠BAE-∠BAC=360°-140°-140°=80°,
又∵△ADC是△ABC沿着AC边翻折180°形成的,
∴∠ACD=∠E=15°,而∠α+∠E=∠EAC+∠ACD,
∴∠α=∠EAC=80°.故答案为80°.
19.解:当4为腰,9为底时,∵4+4<9,∴不能构成三角形;
当腰为9时,∵9+9>4,∴能构成三角形,
∴等腰三角形的周长为:9+9+4=22.
20.解:如图所示:
共同特点:它们的对称轴均为经过两圆圆心的一条直线.
21.解:如图所示,点O为所求作的点.
22.解:将长方形ABCD沿EF,GH同时折叠,B、C两点恰好都落在AD边的P点处,
,,
的周长为,,
.
又,∴长方形ABCD的面积为:.
23.解:,,
由翻折的性质,得
.
24.解:如下图,
25.(1)如图,△A′BC就是所求的图形.
(2)如图:D1、D2、D3、D4就是所求的点.
26.
解:(2)证明:如图1,作DE⊥BA交BA延长线于E,DF⊥BC于F.
∵BD平分∠EBF,DE⊥BE,DF⊥BF,∴DE=DF,
∵∠BAD+∠C=180°,∠BAD+∠EAD=180°,∴∠DAE=∠C,
在△DEA和△DFC中,
∴△DEA≌△DFC(AAS),∴AD=CD.
(3)证明:如图2,在BC时截取BK=BD,连接DK,
∵AB=AC,∠BAC=100°,∴∠ABC=∠C=40°.
∵BD平分∠ABC,∴∠DBK=∠ABC=20°.
∵BD=BK,∴∠BKD=∠BDK=80°,即∠A+∠BKD=180°,
由(2)的结论得AD=DK,
∵∠BKD=180°-∠DKC=∠C+∠KDC,
∴∠KDC=∠C=40°,∴DK=CK,
∴AD=DK=CK,∴BD+AD=BK+CK=BC.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
