8.1基本立体图形-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册讲义(机构适用)(含答案)
文档属性
| 名称 | 8.1基本立体图形-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册讲义(机构适用)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 140.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-23 08:28:59 | ||
图片预览



文档简介
高中数学必修第二册第八章立体几何初步(人教A版2019)
8.1基本立体图形
【基础梳理】
要点一、棱柱的结构特征
一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互侧相平行,由这些面所围成的几何体叫做棱柱.
在棱柱中,两个互相平行的面叫做棱柱的底面,简称底;其余各面叫做棱柱的侧面,相邻侧面的公共边叫做棱柱的侧棱;侧面与底面的公共顶点叫做棱柱的顶点.
要点二、棱锥的结构特征
一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥 .这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点.相邻侧面的公共边叫做棱锥的侧棱;
要点三、圆柱的结构特征
以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱.旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;平行于轴的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线.
要点四、圆锥的结构特征
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体叫做圆锥.圆锥也有轴、底面、侧面和母线.
要点五、棱台于圆台的结构特征
用一个平行于棱锥底面的平面去截棱锥,底面和截面之间那部分,这样的几何体叫做棱台.在棱台中,原棱锥的底面和截面分别叫做棱台的下底面和上底面,棱台也有侧面、侧棱、顶点.
用一个平行于圆锥底面的平面曲截圆锥,底面与截面之间的部分,这样的几何体叫做圆台.
要点六、球的结构
以半圆的直径所在直线为旋转轴.半圆面旋转一周形成的几何体叫做球体.简称球.半圆的圆心叫做球的球心.半圆的半径叫做球的半径.半圆的直径叫做球的直径
【课堂探究】
例1.《九章算术》中,称底面为矩形且有一侧棱垂直于底面的四棱锥为阳马.设 AA1 是正八棱柱的一条侧棱,如图,若阳马以该正八棱柱的顶点为顶点,以 AA1 为底面矩形的一边,则这样的阳马的个数是(??? )
A.?8?????????????????????????????????????????B.?16?????????????????????????????????????????C.?24?????????????????????????????????????????D.?28
例2如图,在直三棱柱 ABC?A1B1C1 中,底面为直角三角形, ∠ACB=90° , AC=6 , BC=CC1=2 ,点 P 是线段 BC1 上一动点,则 CP+PA1 的最小值是(?? )
A.?26??????????????????????????????????B.?52??????????????????????????????????C.?37+1??????????????????????????????????D.?6+2
【课后练习】
1.圆锥的底面直径为2,它的侧面展开图是一个半圆,则该圆锥的高为(??? )
A.?3?????????????????????????????????????????B.?2?????????????????????????????????????????C.?23?????????????????????????????????????????D.?4
2.下列说法正确的是(??? )
A.?通过圆台侧面上一点可以做出无数条母线
B.?直角三角形绕其一边所在直线旋转一周得到的几何体是圆锥
C.?圆柱的上底面下底面互相平行
D.?五棱锥只有五条棱
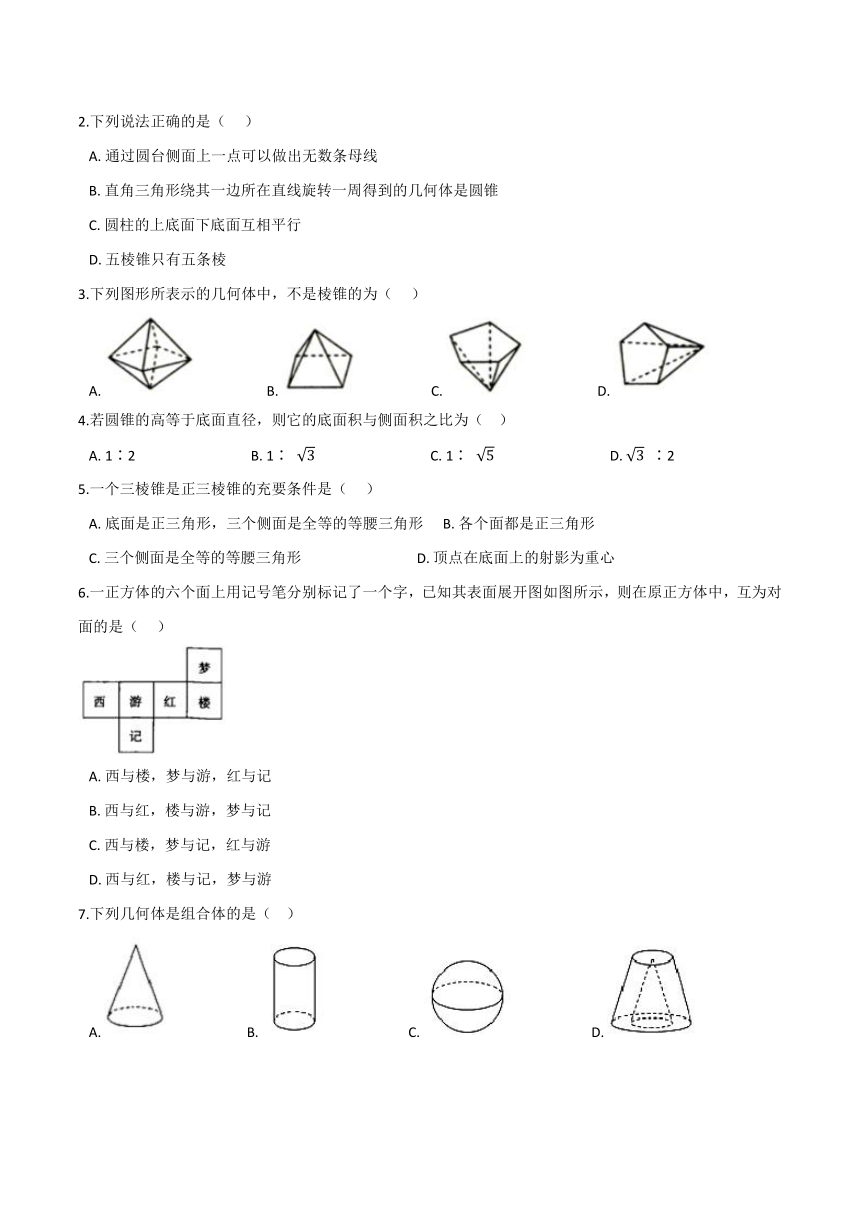
3.下列图形所表示的几何体中,不是棱锥的为(??? )
A.?????????????????????B.?????????????????????C.?????????????????????D.?
4.若圆锥的高等于底面直径,则它的底面积与侧面积之比为(?? )
A.?1∶2?????????????????????????????????B.?1∶ 3?????????????????????????????????C.?1∶ 5?????????????????????????????????D.?3 ∶2
5.一个三棱锥是正三棱锥的充要条件是(??? )
A.?底面是正三角形,三个侧面是全等的等腰三角形?????B.?各个面都是正三角形
C.?三个侧面是全等的等腰三角形?????????????????????????????????D.?顶点在底面上的射影为重心
6.一正方体的六个面上用记号笔分别标记了一个字,已知其表面展开图如图所示,则在原正方体中,互为对面的是(??? )
A.?西与楼,梦与游,红与记
B.?西与红,楼与游,梦与记
C.?西与楼,梦与记,红与游
D.?西与红,楼与记,梦与游
7.下列几何体是组合体的是(?? )
A.????????????????????????B.????????????????????????C.????????????????????????D.?
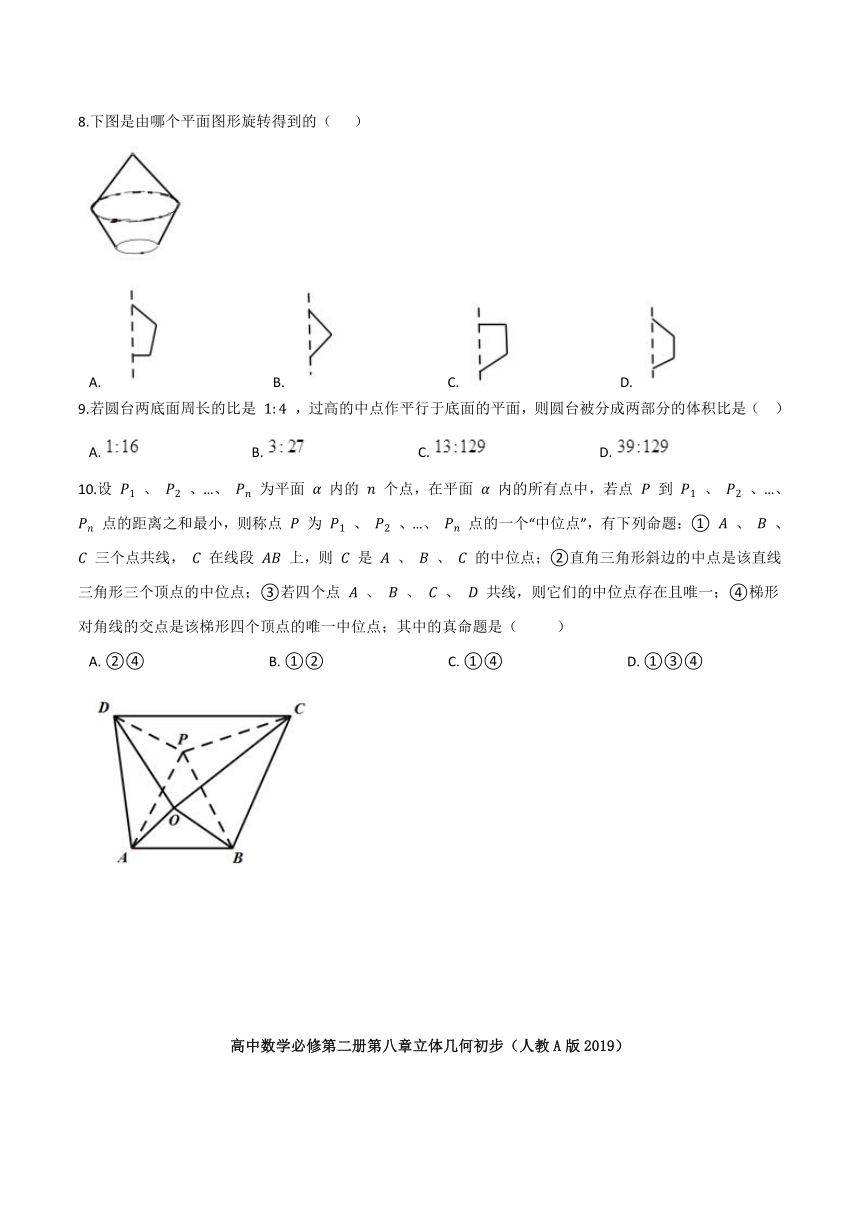
8.下图是由哪个平面图形旋转得到的(???? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
9.若圆台两底面周长的比是 1:4 ,过高的中点作平行于底面的平面,则圆台被分成两部分的体积比是(?? )
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
10.设 P1 、 P2 、…、 Pn 为平面 α 内的 n 个点,在平面 α 内的所有点中,若点 P 到 P1 、 P2 、…、 Pn 点的距离之和最小,则称点 P 为 P1 、 P2 、…、 Pn 点的一个“中位点”,有下列命题:① A 、 B 、 C 三个点共线, C 在线段 AB 上,则 C 是 A 、 B 、 C 的中位点;②直角三角形斜边的中点是该直线三角形三个顶点的中位点;③若四个点 A 、 B 、 C 、 D 共线,则它们的中位点存在且唯一;④梯形对角线的交点是该梯形四个顶点的唯一中位点;其中的真命题是(????????? )
A.?②④????????????????????????????????????B.?①②????????????????????????????????????C.?①④????????????????????????????????????D.?①③④
高中数学必修第二册第八章立体几何初步(人教A版2019)
8.1基本立体图形
【基础梳理】
要点一、棱柱的结构特征
一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互侧相平行,由这些面所围成的几何体叫做棱柱.
在棱柱中,两个互相平行的面叫做棱柱的底面,简称底;其余各面叫做棱柱的侧面,相邻侧面的公共边叫做棱柱的侧棱;侧面与底面的公共顶点叫做棱柱的顶点.
要点二、棱锥的结构特征
一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥 .这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点.相邻侧面的公共边叫做棱锥的侧棱;
要点三、圆柱的结构特征
以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱.旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;平行于轴的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线.
要点四、圆锥的结构特征
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体叫做圆锥.圆锥也有轴、底面、侧面和母线.
要点五、棱台于圆台的结构特征
用一个平行于棱锥底面的平面去截棱锥,底面和截面之间那部分,这样的几何体叫做棱台.在棱台中,原棱锥的底面和截面分别叫做棱台的下底面和上底面,棱台也有侧面、侧棱、顶点.
用一个平行于圆锥底面的平面曲截圆锥,底面与截面之间的部分,这样的几何体叫做圆台.
要点六、球的结构
以半圆的直径所在直线为旋转轴.半圆面旋转一周形成的几何体叫做球体.简称球.半圆的圆心叫做球的球心.半圆的半径叫做球的半径.半圆的直径叫做球的直径
【课堂探究】
例1.《九章算术》中,称底面为矩形且有一侧棱垂直于底面的四棱锥为阳马.设 AA1 是正八棱柱的一条侧棱,如图,若阳马以该正八棱柱的顶点为顶点,以 AA1 为底面矩形的一边,则这样的阳马的个数是(??? )
A.?8?????????????????????????????????????????B.?16?????????????????????????????????????????C.?24?????????????????????????????????????????D.?28
【答案】 C
【解析】根据正八边形的性质可得,底面边长都相等,底面每个内角都为 135? ,
∠HAG=∠BAC=22.5? , ∠HAF=∠BAD=45? ,所以
AB⊥AF , AC⊥AG , AD⊥AH ,又因为 AA1⊥ 平面 ABCDEFGH ,
且 AA1∩AB=A ,则 AF⊥ 平面 AA1B1B ,又因为 AF // A1F1 // BE // B1E1 ,所以共有4个阳马;
同理, AG⊥ 平面 AA1C1C ,共4个;
AH⊥ 平面 AA1D1D ,共4个;
AB⊥ 平面 AA1F1F ,共4个;
AC⊥ 平面 AA1G1G ,共4个;
AD⊥ 平面 AA1H1H ,共4个;
故有24个阳马.
故答案为:C.
【分析】根据新定义和正八边形的性质和线面垂直的判断方法即可得到答案。
例2如图,在直三棱柱 ABC?A1B1C1 中,底面为直角三角形, ∠ACB=90° , AC=6 , BC=CC1=2 ,点 P 是线段 BC1 上一动点,则 CP+PA1 的最小值是(?? )
A.?26??????????????????????????????????B.?52??????????????????????????????????C.?37+1??????????????????????????????????D.?6+2
【答案】 B
【解析】连A1B,沿BC1将△CBC1展开与△A1BC1在同一个平面内,
连接A1C,长度即是所求.
∵直三棱柱ABC﹣A1B1C1中,底面为直角三角形,∠ACB=90°,AC=6,BC=CC1 =2 ,
∴矩形BCC1B1是边长为 2 的正方形;则BC1=2;
另外A1C1=AC=6;
在矩形ABB1A1中,A1B1=AB= 38 ,BB1 =2 ,则A1B= 40 ;
易发现62+22=40,即A1C12+BC12=A1B2 ,
∴∠A1C1B=90°,则∠A1C1C=135°
A1C =A1C12+C1C2?2A1C1?C1C?cos135°=36+2+2×6?2?22=52
故答案为:B.
【分析】根据题意由三角形的几何关系计算出BC的值进而得出长方体的棱长再由勾股定理和余弦定理代入数值计算出结果即可。
【课后练习】
1.圆锥的底面直径为2,它的侧面展开图是一个半圆,则该圆锥的高为(??? )
A.?3?????????????????????????????????????????B.?2?????????????????????????????????????????C.?23?????????????????????????????????????????D.?4
【答案】 A
【解析】解:设圆锥的母线为 l ,高为 ? ,
依题意可得 πl=2π ,所以 l=2 ,则 ?=l2?r2=22?12=3
故答案为:A
【分析】设圆锥的母线为l,高为h,依题意可得 πl=2π ,即可求出母线,再由勾股定理计算可得;
2.下列说法正确的是(??? )
A.?通过圆台侧面上一点可以做出无数条母线
B.?直角三角形绕其一边所在直线旋转一周得到的几何体是圆锥
C.?圆柱的上底面下底面互相平行
D.?五棱锥只有五条棱
【答案】 C
【解析】A中,根据圆台的结构特征,通过圆台侧面上一点有且只有一条母线,所以不正确;
B中,根据圆锥的定义,直角三角形绕其一直角边所在直线旋转一周得到的几何体是圆锥,所以不正确;
C中,根据圆柱的结构特征,可知圆柱的上底面下底面互相平行,所以是正确的;
D中,根据棱锥的结构特征,可得五棱锥只有五条侧棱,所以不正确.
故答案为:C.
【分析】根据圆柱、圆锥和圆台的几何结构特征,逐项判定,即可求解.
3.下列图形所表示的几何体中,不是棱锥的为(??? )
A.?????????????????????B.?????????????????????C.?????????????????????D.?
【答案】 A
【解析】棱锥的定义为:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥.
根据棱锥的定义,B 、C 、D选项中的几何图形是棱锥,A选项中的几何图形是由两个棱锥组合而成的,所以不是棱锥;
故答案为:A
【分析】根据棱锥的定义结合结合图形分析可得答案.
4.若圆锥的高等于底面直径,则它的底面积与侧面积之比为(?? )
A.?1∶2?????????????????????????????????B.?1∶ 3?????????????????????????????????C.?1∶ 5?????????????????????????????????D.?3 ∶2
【答案】 C
【解析】设圆锥底面半径为r,则高h=2r,∴其母线长l= r.∴S侧=πrl= πr2 , S底=πr.
故答案为:C.
【分析】由已知,求出圆锥的母线长,进而求出圆锥的底面面积和侧面积,可得答案
5.一个三棱锥是正三棱锥的充要条件是(??? )
A.?底面是正三角形,三个侧面是全等的等腰三角形?????B.?各个面都是正三角形
C.?三个侧面是全等的等腰三角形?????????????????????????????????D.?顶点在底面上的射影为重心
【答案】 A
【解析】A.根据正三棱锥的定义可知,满足侧面是全等的等腰三角形,底面是正三角形的三棱锥是正三棱锥.正三棱锥的底面是正三角形,三个侧面是全等的等腰三角形,所以一个三棱锥是正三棱锥的充要条件是底面是正三角形,三个侧面是全等的等腰三角形,所以该选项符合题意;
B. 各个面都是正三角形,则三棱锥是正三棱锥,所以各个面都是正三角形是三棱锥为正三棱锥的充分条件;如果三棱锥是正三棱锥,则各个面不一定都是正三角形,所以各个面都是正三角形是三棱锥为正三棱锥的非必要条件,故该选项错误.
C. 三个侧面是全等的等腰三角形不一定是正三棱锥,如图所示,VA=VC=BC=AB,AC=VB时,不一定是正三棱锥,故该选项错误;
D. 顶点在底面上的射影为重心,设底面为直角三角形 ABC ,其重心为 O ,过点 O 作平面ABC的垂线 OV ,连接VA,VB,VC得到三棱锥V-ABC,显然三棱锥V-ABC不是正三棱锥,所以该选项错误.
故答案为:A
【分析】利用正三棱锥和充要条件的定义逐一分析判断每一个选项得解.
6.一正方体的六个面上用记号笔分别标记了一个字,已知其表面展开图如图所示,则在原正方体中,互为对面的是(??? )
A.?西与楼,梦与游,红与记
B.?西与红,楼与游,梦与记
C.?西与楼,梦与记,红与游
D.?西与红,楼与记,梦与游
【答案】 B
【解析】以红为底,折叠正方体后,即可判断出:
西与红,楼与游,梦与记互为对面.
故答案为:B
【分析】将该正方体折叠,即可判断对立面的字.
7.下列几何体是组合体的是(?? )
A.????????????????????????B.????????????????????????C.????????????????????????D.?
【答案】 D
【解析】A,B,C分别是圆锥、圆柱、球,都为简单几何体;D为圆台去掉一个圆锥,为组合体,
故答案为:D.
【分析】利用组合体的概念进行判断,即可得结果.
8.下图是由哪个平面图形旋转得到的(???? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
【答案】 A
【解析】根据下面是圆台,上方是圆锥,可知应选A.
故答案为:A
【分析】利用旋转体的构成平面找出正确的选项。
9.若圆台两底面周长的比是 1:4 ,过高的中点作平行于底面的平面,则圆台被分成两部分的体积比是(?? )
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
【答案】 D
【解析】由题意设上、下底面半径分别为r,4r,
截面半径为x,圆台的高为2h,则有 x?r3r=12 ,
∴ x=52r. ?
∴ V上V下=13π?(r2+rx+x2)13π?(x2+4rx+16r2)=39129 ?.
故答案为:D.
【分析】本题主要考查圆台的体积公式,由圆台体积公式即可得出结果。
10.设 P1 、 P2 、…、 Pn 为平面 α 内的 n 个点,在平面 α 内的所有点中,若点 P 到 P1 、 P2 、…、 Pn 点的距离之和最小,则称点 P 为 P1 、 P2 、…、 Pn 点的一个“中位点”,有下列命题:① A 、 B 、 C 三个点共线, C 在线段 AB 上,则 C 是 A 、 B 、 C 的中位点;②直角三角形斜边的中点是该直线三角形三个顶点的中位点;③若四个点 A 、 B 、 C 、 D 共线,则它们的中位点存在且唯一;④梯形对角线的交点是该梯形四个顶点的唯一中位点;其中的真命题是(????????? )
A.?②④????????????????????????????????????B.?①②????????????????????????????????????C.?①④????????????????????????????????????D.?①③④
【答案】 C
【解析】①若三个点 A,B,C 共线, C 在线段 AB 上,根据两点之间线段最短,
则 C 是 A,B,C 的中位点,正确;②举一个反例,如边长为 3,4,5 的直角三角形 ABC ,此直角三角形的斜边的中点到三个顶点的距离之和为 5+2.5=7.5 ,而直角顶点到三个顶点的距离之和为7,
∴直角三角形斜边的中点不是该直角三角形三个顶点的中位点;故错误;③若四个点 A,B,C,D 共线,则它们的中位点是中间两点连线段上的任意一个点,故它们的中位点存在但不唯一;故错误;④如图,在梯形 ABCD 中,对角线的交点 O, P 是任意一点,则根据三角形两边之和大于第三边得 PA+PB+PC+PD≥AC+BD=OA+OB+OC+OD ,
∴梯形对角线的交点是该梯形四个顶点的唯一中位点.正确.
故①④正确.
故答案为:C
【分析】结合中位线的性质以及空间中点与线的位置关系对选项逐一判断分析或举反例即可得出答案。
8.1基本立体图形
【基础梳理】
要点一、棱柱的结构特征
一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互侧相平行,由这些面所围成的几何体叫做棱柱.
在棱柱中,两个互相平行的面叫做棱柱的底面,简称底;其余各面叫做棱柱的侧面,相邻侧面的公共边叫做棱柱的侧棱;侧面与底面的公共顶点叫做棱柱的顶点.
要点二、棱锥的结构特征
一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥 .这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点.相邻侧面的公共边叫做棱锥的侧棱;
要点三、圆柱的结构特征
以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱.旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;平行于轴的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线.
要点四、圆锥的结构特征
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体叫做圆锥.圆锥也有轴、底面、侧面和母线.
要点五、棱台于圆台的结构特征
用一个平行于棱锥底面的平面去截棱锥,底面和截面之间那部分,这样的几何体叫做棱台.在棱台中,原棱锥的底面和截面分别叫做棱台的下底面和上底面,棱台也有侧面、侧棱、顶点.
用一个平行于圆锥底面的平面曲截圆锥,底面与截面之间的部分,这样的几何体叫做圆台.
要点六、球的结构
以半圆的直径所在直线为旋转轴.半圆面旋转一周形成的几何体叫做球体.简称球.半圆的圆心叫做球的球心.半圆的半径叫做球的半径.半圆的直径叫做球的直径
【课堂探究】
例1.《九章算术》中,称底面为矩形且有一侧棱垂直于底面的四棱锥为阳马.设 AA1 是正八棱柱的一条侧棱,如图,若阳马以该正八棱柱的顶点为顶点,以 AA1 为底面矩形的一边,则这样的阳马的个数是(??? )
A.?8?????????????????????????????????????????B.?16?????????????????????????????????????????C.?24?????????????????????????????????????????D.?28
例2如图,在直三棱柱 ABC?A1B1C1 中,底面为直角三角形, ∠ACB=90° , AC=6 , BC=CC1=2 ,点 P 是线段 BC1 上一动点,则 CP+PA1 的最小值是(?? )
A.?26??????????????????????????????????B.?52??????????????????????????????????C.?37+1??????????????????????????????????D.?6+2
【课后练习】
1.圆锥的底面直径为2,它的侧面展开图是一个半圆,则该圆锥的高为(??? )
A.?3?????????????????????????????????????????B.?2?????????????????????????????????????????C.?23?????????????????????????????????????????D.?4
2.下列说法正确的是(??? )
A.?通过圆台侧面上一点可以做出无数条母线
B.?直角三角形绕其一边所在直线旋转一周得到的几何体是圆锥
C.?圆柱的上底面下底面互相平行
D.?五棱锥只有五条棱
3.下列图形所表示的几何体中,不是棱锥的为(??? )
A.?????????????????????B.?????????????????????C.?????????????????????D.?
4.若圆锥的高等于底面直径,则它的底面积与侧面积之比为(?? )
A.?1∶2?????????????????????????????????B.?1∶ 3?????????????????????????????????C.?1∶ 5?????????????????????????????????D.?3 ∶2
5.一个三棱锥是正三棱锥的充要条件是(??? )
A.?底面是正三角形,三个侧面是全等的等腰三角形?????B.?各个面都是正三角形
C.?三个侧面是全等的等腰三角形?????????????????????????????????D.?顶点在底面上的射影为重心
6.一正方体的六个面上用记号笔分别标记了一个字,已知其表面展开图如图所示,则在原正方体中,互为对面的是(??? )
A.?西与楼,梦与游,红与记
B.?西与红,楼与游,梦与记
C.?西与楼,梦与记,红与游
D.?西与红,楼与记,梦与游
7.下列几何体是组合体的是(?? )
A.????????????????????????B.????????????????????????C.????????????????????????D.?
8.下图是由哪个平面图形旋转得到的(???? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
9.若圆台两底面周长的比是 1:4 ,过高的中点作平行于底面的平面,则圆台被分成两部分的体积比是(?? )
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
10.设 P1 、 P2 、…、 Pn 为平面 α 内的 n 个点,在平面 α 内的所有点中,若点 P 到 P1 、 P2 、…、 Pn 点的距离之和最小,则称点 P 为 P1 、 P2 、…、 Pn 点的一个“中位点”,有下列命题:① A 、 B 、 C 三个点共线, C 在线段 AB 上,则 C 是 A 、 B 、 C 的中位点;②直角三角形斜边的中点是该直线三角形三个顶点的中位点;③若四个点 A 、 B 、 C 、 D 共线,则它们的中位点存在且唯一;④梯形对角线的交点是该梯形四个顶点的唯一中位点;其中的真命题是(????????? )
A.?②④????????????????????????????????????B.?①②????????????????????????????????????C.?①④????????????????????????????????????D.?①③④
高中数学必修第二册第八章立体几何初步(人教A版2019)
8.1基本立体图形
【基础梳理】
要点一、棱柱的结构特征
一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互侧相平行,由这些面所围成的几何体叫做棱柱.
在棱柱中,两个互相平行的面叫做棱柱的底面,简称底;其余各面叫做棱柱的侧面,相邻侧面的公共边叫做棱柱的侧棱;侧面与底面的公共顶点叫做棱柱的顶点.
要点二、棱锥的结构特征
一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥 .这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点.相邻侧面的公共边叫做棱锥的侧棱;
要点三、圆柱的结构特征
以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱.旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;平行于轴的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线.
要点四、圆锥的结构特征
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体叫做圆锥.圆锥也有轴、底面、侧面和母线.
要点五、棱台于圆台的结构特征
用一个平行于棱锥底面的平面去截棱锥,底面和截面之间那部分,这样的几何体叫做棱台.在棱台中,原棱锥的底面和截面分别叫做棱台的下底面和上底面,棱台也有侧面、侧棱、顶点.
用一个平行于圆锥底面的平面曲截圆锥,底面与截面之间的部分,这样的几何体叫做圆台.
要点六、球的结构
以半圆的直径所在直线为旋转轴.半圆面旋转一周形成的几何体叫做球体.简称球.半圆的圆心叫做球的球心.半圆的半径叫做球的半径.半圆的直径叫做球的直径
【课堂探究】
例1.《九章算术》中,称底面为矩形且有一侧棱垂直于底面的四棱锥为阳马.设 AA1 是正八棱柱的一条侧棱,如图,若阳马以该正八棱柱的顶点为顶点,以 AA1 为底面矩形的一边,则这样的阳马的个数是(??? )
A.?8?????????????????????????????????????????B.?16?????????????????????????????????????????C.?24?????????????????????????????????????????D.?28
【答案】 C
【解析】根据正八边形的性质可得,底面边长都相等,底面每个内角都为 135? ,
∠HAG=∠BAC=22.5? , ∠HAF=∠BAD=45? ,所以
AB⊥AF , AC⊥AG , AD⊥AH ,又因为 AA1⊥ 平面 ABCDEFGH ,
且 AA1∩AB=A ,则 AF⊥ 平面 AA1B1B ,又因为 AF // A1F1 // BE // B1E1 ,所以共有4个阳马;
同理, AG⊥ 平面 AA1C1C ,共4个;
AH⊥ 平面 AA1D1D ,共4个;
AB⊥ 平面 AA1F1F ,共4个;
AC⊥ 平面 AA1G1G ,共4个;
AD⊥ 平面 AA1H1H ,共4个;
故有24个阳马.
故答案为:C.
【分析】根据新定义和正八边形的性质和线面垂直的判断方法即可得到答案。
例2如图,在直三棱柱 ABC?A1B1C1 中,底面为直角三角形, ∠ACB=90° , AC=6 , BC=CC1=2 ,点 P 是线段 BC1 上一动点,则 CP+PA1 的最小值是(?? )
A.?26??????????????????????????????????B.?52??????????????????????????????????C.?37+1??????????????????????????????????D.?6+2
【答案】 B
【解析】连A1B,沿BC1将△CBC1展开与△A1BC1在同一个平面内,
连接A1C,长度即是所求.
∵直三棱柱ABC﹣A1B1C1中,底面为直角三角形,∠ACB=90°,AC=6,BC=CC1 =2 ,
∴矩形BCC1B1是边长为 2 的正方形;则BC1=2;
另外A1C1=AC=6;
在矩形ABB1A1中,A1B1=AB= 38 ,BB1 =2 ,则A1B= 40 ;
易发现62+22=40,即A1C12+BC12=A1B2 ,
∴∠A1C1B=90°,则∠A1C1C=135°
A1C =A1C12+C1C2?2A1C1?C1C?cos135°=36+2+2×6?2?22=52
故答案为:B.
【分析】根据题意由三角形的几何关系计算出BC的值进而得出长方体的棱长再由勾股定理和余弦定理代入数值计算出结果即可。
【课后练习】
1.圆锥的底面直径为2,它的侧面展开图是一个半圆,则该圆锥的高为(??? )
A.?3?????????????????????????????????????????B.?2?????????????????????????????????????????C.?23?????????????????????????????????????????D.?4
【答案】 A
【解析】解:设圆锥的母线为 l ,高为 ? ,
依题意可得 πl=2π ,所以 l=2 ,则 ?=l2?r2=22?12=3
故答案为:A
【分析】设圆锥的母线为l,高为h,依题意可得 πl=2π ,即可求出母线,再由勾股定理计算可得;
2.下列说法正确的是(??? )
A.?通过圆台侧面上一点可以做出无数条母线
B.?直角三角形绕其一边所在直线旋转一周得到的几何体是圆锥
C.?圆柱的上底面下底面互相平行
D.?五棱锥只有五条棱
【答案】 C
【解析】A中,根据圆台的结构特征,通过圆台侧面上一点有且只有一条母线,所以不正确;
B中,根据圆锥的定义,直角三角形绕其一直角边所在直线旋转一周得到的几何体是圆锥,所以不正确;
C中,根据圆柱的结构特征,可知圆柱的上底面下底面互相平行,所以是正确的;
D中,根据棱锥的结构特征,可得五棱锥只有五条侧棱,所以不正确.
故答案为:C.
【分析】根据圆柱、圆锥和圆台的几何结构特征,逐项判定,即可求解.
3.下列图形所表示的几何体中,不是棱锥的为(??? )
A.?????????????????????B.?????????????????????C.?????????????????????D.?
【答案】 A
【解析】棱锥的定义为:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥.
根据棱锥的定义,B 、C 、D选项中的几何图形是棱锥,A选项中的几何图形是由两个棱锥组合而成的,所以不是棱锥;
故答案为:A
【分析】根据棱锥的定义结合结合图形分析可得答案.
4.若圆锥的高等于底面直径,则它的底面积与侧面积之比为(?? )
A.?1∶2?????????????????????????????????B.?1∶ 3?????????????????????????????????C.?1∶ 5?????????????????????????????????D.?3 ∶2
【答案】 C
【解析】设圆锥底面半径为r,则高h=2r,∴其母线长l= r.∴S侧=πrl= πr2 , S底=πr.
故答案为:C.
【分析】由已知,求出圆锥的母线长,进而求出圆锥的底面面积和侧面积,可得答案
5.一个三棱锥是正三棱锥的充要条件是(??? )
A.?底面是正三角形,三个侧面是全等的等腰三角形?????B.?各个面都是正三角形
C.?三个侧面是全等的等腰三角形?????????????????????????????????D.?顶点在底面上的射影为重心
【答案】 A
【解析】A.根据正三棱锥的定义可知,满足侧面是全等的等腰三角形,底面是正三角形的三棱锥是正三棱锥.正三棱锥的底面是正三角形,三个侧面是全等的等腰三角形,所以一个三棱锥是正三棱锥的充要条件是底面是正三角形,三个侧面是全等的等腰三角形,所以该选项符合题意;
B. 各个面都是正三角形,则三棱锥是正三棱锥,所以各个面都是正三角形是三棱锥为正三棱锥的充分条件;如果三棱锥是正三棱锥,则各个面不一定都是正三角形,所以各个面都是正三角形是三棱锥为正三棱锥的非必要条件,故该选项错误.
C. 三个侧面是全等的等腰三角形不一定是正三棱锥,如图所示,VA=VC=BC=AB,AC=VB时,不一定是正三棱锥,故该选项错误;
D. 顶点在底面上的射影为重心,设底面为直角三角形 ABC ,其重心为 O ,过点 O 作平面ABC的垂线 OV ,连接VA,VB,VC得到三棱锥V-ABC,显然三棱锥V-ABC不是正三棱锥,所以该选项错误.
故答案为:A
【分析】利用正三棱锥和充要条件的定义逐一分析判断每一个选项得解.
6.一正方体的六个面上用记号笔分别标记了一个字,已知其表面展开图如图所示,则在原正方体中,互为对面的是(??? )
A.?西与楼,梦与游,红与记
B.?西与红,楼与游,梦与记
C.?西与楼,梦与记,红与游
D.?西与红,楼与记,梦与游
【答案】 B
【解析】以红为底,折叠正方体后,即可判断出:
西与红,楼与游,梦与记互为对面.
故答案为:B
【分析】将该正方体折叠,即可判断对立面的字.
7.下列几何体是组合体的是(?? )
A.????????????????????????B.????????????????????????C.????????????????????????D.?
【答案】 D
【解析】A,B,C分别是圆锥、圆柱、球,都为简单几何体;D为圆台去掉一个圆锥,为组合体,
故答案为:D.
【分析】利用组合体的概念进行判断,即可得结果.
8.下图是由哪个平面图形旋转得到的(???? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
【答案】 A
【解析】根据下面是圆台,上方是圆锥,可知应选A.
故答案为:A
【分析】利用旋转体的构成平面找出正确的选项。
9.若圆台两底面周长的比是 1:4 ,过高的中点作平行于底面的平面,则圆台被分成两部分的体积比是(?? )
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
【答案】 D
【解析】由题意设上、下底面半径分别为r,4r,
截面半径为x,圆台的高为2h,则有 x?r3r=12 ,
∴ x=52r. ?
∴ V上V下=13π?(r2+rx+x2)13π?(x2+4rx+16r2)=39129 ?.
故答案为:D.
【分析】本题主要考查圆台的体积公式,由圆台体积公式即可得出结果。
10.设 P1 、 P2 、…、 Pn 为平面 α 内的 n 个点,在平面 α 内的所有点中,若点 P 到 P1 、 P2 、…、 Pn 点的距离之和最小,则称点 P 为 P1 、 P2 、…、 Pn 点的一个“中位点”,有下列命题:① A 、 B 、 C 三个点共线, C 在线段 AB 上,则 C 是 A 、 B 、 C 的中位点;②直角三角形斜边的中点是该直线三角形三个顶点的中位点;③若四个点 A 、 B 、 C 、 D 共线,则它们的中位点存在且唯一;④梯形对角线的交点是该梯形四个顶点的唯一中位点;其中的真命题是(????????? )
A.?②④????????????????????????????????????B.?①②????????????????????????????????????C.?①④????????????????????????????????????D.?①③④
【答案】 C
【解析】①若三个点 A,B,C 共线, C 在线段 AB 上,根据两点之间线段最短,
则 C 是 A,B,C 的中位点,正确;②举一个反例,如边长为 3,4,5 的直角三角形 ABC ,此直角三角形的斜边的中点到三个顶点的距离之和为 5+2.5=7.5 ,而直角顶点到三个顶点的距离之和为7,
∴直角三角形斜边的中点不是该直角三角形三个顶点的中位点;故错误;③若四个点 A,B,C,D 共线,则它们的中位点是中间两点连线段上的任意一个点,故它们的中位点存在但不唯一;故错误;④如图,在梯形 ABCD 中,对角线的交点 O, P 是任意一点,则根据三角形两边之和大于第三边得 PA+PB+PC+PD≥AC+BD=OA+OB+OC+OD ,
∴梯形对角线的交点是该梯形四个顶点的唯一中位点.正确.
故①④正确.
故答案为:C
【分析】结合中位线的性质以及空间中点与线的位置关系对选项逐一判断分析或举反例即可得出答案。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
