8.2 全等三角形学案

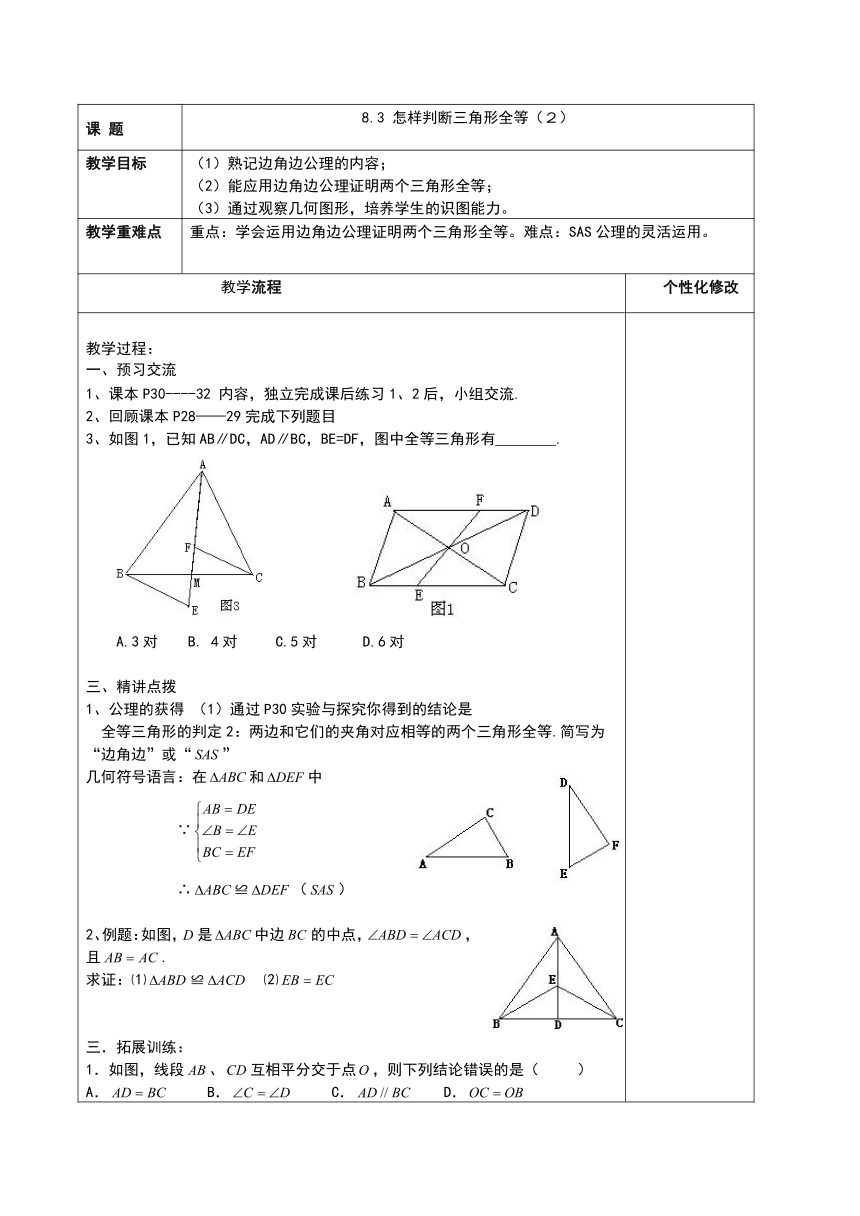
课 题 8.3 怎样判断三角形全等（２）
教学目标 （1）熟记边角边公理的内容；（2）能应用边角边公理证明两个三角形全等；（3）通过观察几何图形，培养学生的识图能力。
教学重难点 重点：学会运用边角边公理证明两个三角形全等。难点：SAS公理的灵活运用。
教学流程 个性化修改
教学过程：预习交流1、课本P30----32 内容，独立完成课后练习1、2后，小组交流.2、回顾课本P28——29完成下列题目3、如图1，已知AB∥DC，AD∥BC，BE=DF，图中全等三角形有 . A.3对 B. 4对 C.5对 D.6对　　　　　三、精讲点拨1、公理的获得 （1）通过P30实验与探究你得到的结论是 全等三角形的判定2：两边和它们的夹角对应相等的两个三角形全等.简写为“边角边”或“”几何符号语言：在和中 ∵∴≌（）2、例题：如图，是中边的中点，，且.求证：⑴≌ ⑵三．拓展训练：1．如图，线段、互相平分交于点，则下列结论错误的是（ ）A． B． C． D．2．如图，已知，.求证：≌3．如图，于，于，，.求证：4．点、、、在同一直线上，，且.求证：⑴≌ ⑵四、巩固练习（公理的应用）1、如图所示，在△ABC中，已知AB=AC，延长AB到D，使BD=AB，延长AC到E，使CE=AC，连结CD、BE，求证：CD=BE.五、系统小结： 六、限时作业1、如图，已知点A、B、C、D在同一条直线上，AB=CD，∠D=∠ECA，EC=FD，求证：AE=BF。2、如图，已知AB＝AC，AD＝AE，∠1＝∠2，BE与CD相等吗？为什么？
教学反思：