第二章平面向量阶段提升 课件(共28张PPT)2020-2021学年高一下学期数学人教A版必修4
文档属性
| 名称 | 第二章平面向量阶段提升 课件(共28张PPT)2020-2021学年高一下学期数学人教A版必修4 |

|
|
| 格式 | ppt | ||
| 文件大小 | 603.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-24 11:25:41 | ||
图片预览








文档简介
(共28张PPT)
阶段提升课
第三课 平
面
向
量
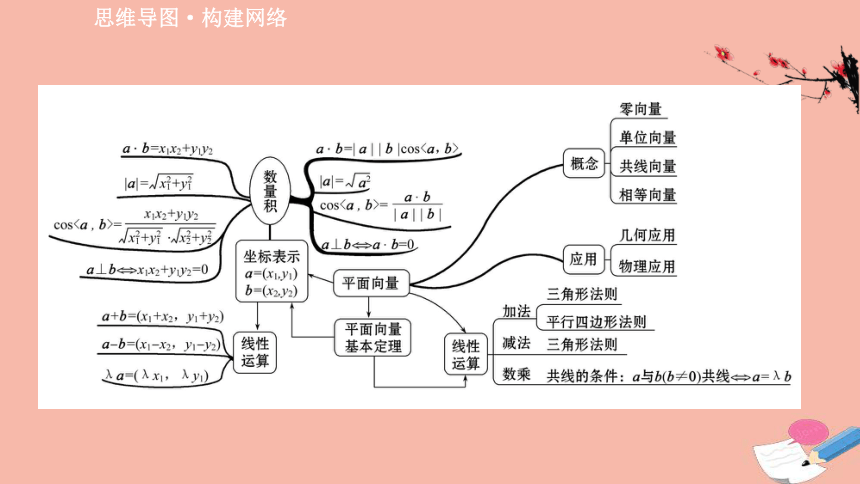
思维导图·构建网络
考点整合·素养提升
题组训练一 平面向量的线性运算及其应用?
1.对于向量m=(x1,y1),n=(x2,y2),定义m?n=(x1x2,y1y2).已知a=(2,-4),且a+b=a?b,那么向量b等于
( )
【解析】选A.设b=(x,y),由新定义及a+b=a?b,可得(2+x,y-4)=(2x,-4y),
所以向量b=
.
2.在平行四边形ABCD中,E和F分别是边CD和BC的中点.若
其中
λ,μ∈R,求λ+μ的值.
【解析】选择
作为平面向量的一组基底,
则
又
【方法技巧】
(1)向量的线性运算主要是运用它们的运算法则、运算律,解决三点共线、两线段平行、线段相等、求点或向量的坐标等问题,而理解相关概念,用基底或用坐标表示向量是基础.
(2)向量是一个有“形”的几何量,因此在研究向量的有关问题时,一定要结合图形进行分析判断求解,特别是平行四边形法则和三角形法则的应用.
题组训练二 平面向量数量积的运算?
1.已知a=(2,-1),a+2b=(6,3),若b·c=14,|c|=5,则向量c的坐标为________.?
【解析】因为2b=(a+2b)-a=(6,3)-(2,-1)=(4,4),
所以b=(2,2).设c=(x,y),
则由题可知
解得
所以c=(3,4)或c=(4,3).
答案:(3,4)或(4,3)
2.已知|a|=1,|b|=
.
(1)若a∥b,求a·b.
(2)若a,b的夹角为60°,求|a+b|.
(3)若(2a-b)⊥b,求a与b的夹角.
【解析】(1)若a∥b,则a与b的夹角为0或π.
所以a·b=|a||b|cos
0=1×
×1=
或a·b=|a||b|·cos
π=-
.
(2)因为|a+b|2=a2+2a·b+b2=|a|2+2|a||b|cos
60
°+|b|2=1+2×1×
×
+2=3+
,
所以|a+b|=
(3)设a与b的夹角为θ.若(2a-b)⊥b,则(2a-b)·b=0,
即2a·b-b2=0,
所以2|a||b|cos
θ-|b|2=0,
即2×
cos
θ-2=0,
所以cos
θ=
又0≤θ≤π,所以θ=
【方法技巧】向量数量积的两种运算方法
(1)当已知向量的模和夹角时,可利用定义法求解,即a·b=|a|·|b|cos.
(2)当已知向量的坐标时,可利用坐标法求解,即若a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2.
运用两向量的数量积解决长度、夹角、垂直等问题,解题时应灵活选择相应公式求解.
题组训练三 平面向量的平行与垂直?
1.已知A(-2,1),B(6,-3),C(0,5),则△ABC的形状是
( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
【解析】选A.因为
=(8,-4),
=(2,4),
所以
·
=8×2+(-4)×4=0,
所以
⊥
,所以∠BAC=90°,
故△ABC是直角三角形.
2.已知向量
与
的夹角为120°,且|
|=3,|
|=2.若
且
则实数λ的值为________.?
【解析】由
知
=0,
即
=(λ
)·(
)
=(λ-1)
=(λ-1)×3×2×
-λ×9+4=0,解得λ=
.
答案:
【方法技巧】
1.证明共线问题常用的方法
(1)向量a,b(a≠0)共线?存在唯一实数λ,使b=λa.
(2)向量a=(x1,y1),b=(x2,y2)共线?x1y2-x2y1=0.
(3)向量a与b共线?存在不全为零的实数λ1,λ2,使λ1a+λ2b=0.
2.证明平面向量垂直问题的常用方法
a⊥b?a·b=0?x1x2+y1y2=0,
其中a=(x1,y1),b=(x2,y2),且a,b为非零向量.
题组训练四 平面向量的模、夹角?
1.设|a|=|b|=1,|3a-2b|=3,则|3a+b|的值为________.?
【解析】方法一:因为|3a-2b|=3,
所以9a2-12a·b+4b2=9.
又因为|a|=|b|=1,所以a·b=
.
所以|3a+b|2=(3a+b)2
=9a2+6a·b+b2
=9+6×
+1=12.
所以|3a+b|=2
.
方法二:设a=(x1,y1),b=(x2,y2).
因为|a|=|b|=1,
所以
因为3a-2b=(3x1-2x2,3y1-2y2),
所以|3a-2b|=
所以x1x2+y1y2=
.
所以|3a+b|=
答案:2
2.已知平面内三点A(1,0),B(0,1),C(2,5),求:
(1)|2
|.
(2)
与
夹角的余弦值.
(3)与
垂直的单位向量的坐标.
【解析】(1)由题意可得,
=(-1,1),
=(1,5),
所以2
=(-1,7),
所以|2
|=
(2)设
与
的夹角为θ,
则cos
θ=
(3)设与
垂直的单位向量的坐标为(x,y),因为
·(x,y)=(2,4)·(x,y)
=2x+4y=0,且x2+y2=1,
所以要求的向量的坐标为
【方法技巧】
1.夹角问题
求向量a,b夹角θ的步骤:
(1)求|a|,|b|,a·b;
(2)求cos
θ=
(夹角公式);
(3)结合θ的范围[0,π]确定θ的大小.因此求向量的夹角先转化为求向量夹
角的余弦值,再结合夹角的范围确定夹角的大小.
2.有关向量的模长问题
(1)若a=(x,y),则|a|2=x2+y2,或|a|=
(2)若向量a无坐标,则利用平方法,即|a|2=a2;
|a±b|2=a2±2a·b+b2.
题组训练五 平面向量在几何和物理方面的应用?
1.点P在平面上做匀速直线运动,速度v=(4,-3),设开始时点P的坐标为(-10,10),则5秒后点P的坐标为(速度单位:m/s,长度单位:m)( )
A.(-2,4)
B.(-30,25)
C.(10,-5)
D.(5,-10)
【解析】选C.5秒后点P的坐标为(-10,10)+5(4,-3)=(10,-5).
2.如图所示,P是正方形ABCD的对角线BD上一点,四边形PECF是矩形,求证:
(1)PA=EF.
(2)PA⊥EF.
【证明】(1)建立如图所示的平面直角坐标系,设正方形的边长为1,|
|=λ,
则A(0,1),
因为
所以
故PA=EF.
(2)因为
故PA⊥EF.
【方法技巧】
(1)向量的加减运算遵循平行四边形法则或三角形法则,数乘运算和线段平行之间、数量积运算和垂直、夹角、距离问题之间联系密切,因此用向量方法可以解决平面几何中的相关问题.
(2)利用平面向量解决几何问题的关键是恰当地引入向量,通过向量运算,解释几何性质.
(3)物理应用:速度、位移、力、功.
阶段提升课
第三课 平
面
向
量
思维导图·构建网络
考点整合·素养提升
题组训练一 平面向量的线性运算及其应用?
1.对于向量m=(x1,y1),n=(x2,y2),定义m?n=(x1x2,y1y2).已知a=(2,-4),且a+b=a?b,那么向量b等于
( )
【解析】选A.设b=(x,y),由新定义及a+b=a?b,可得(2+x,y-4)=(2x,-4y),
所以向量b=
.
2.在平行四边形ABCD中,E和F分别是边CD和BC的中点.若
其中
λ,μ∈R,求λ+μ的值.
【解析】选择
作为平面向量的一组基底,
则
又
【方法技巧】
(1)向量的线性运算主要是运用它们的运算法则、运算律,解决三点共线、两线段平行、线段相等、求点或向量的坐标等问题,而理解相关概念,用基底或用坐标表示向量是基础.
(2)向量是一个有“形”的几何量,因此在研究向量的有关问题时,一定要结合图形进行分析判断求解,特别是平行四边形法则和三角形法则的应用.
题组训练二 平面向量数量积的运算?
1.已知a=(2,-1),a+2b=(6,3),若b·c=14,|c|=5,则向量c的坐标为________.?
【解析】因为2b=(a+2b)-a=(6,3)-(2,-1)=(4,4),
所以b=(2,2).设c=(x,y),
则由题可知
解得
所以c=(3,4)或c=(4,3).
答案:(3,4)或(4,3)
2.已知|a|=1,|b|=
.
(1)若a∥b,求a·b.
(2)若a,b的夹角为60°,求|a+b|.
(3)若(2a-b)⊥b,求a与b的夹角.
【解析】(1)若a∥b,则a与b的夹角为0或π.
所以a·b=|a||b|cos
0=1×
×1=
或a·b=|a||b|·cos
π=-
.
(2)因为|a+b|2=a2+2a·b+b2=|a|2+2|a||b|cos
60
°+|b|2=1+2×1×
×
+2=3+
,
所以|a+b|=
(3)设a与b的夹角为θ.若(2a-b)⊥b,则(2a-b)·b=0,
即2a·b-b2=0,
所以2|a||b|cos
θ-|b|2=0,
即2×
cos
θ-2=0,
所以cos
θ=
又0≤θ≤π,所以θ=
【方法技巧】向量数量积的两种运算方法
(1)当已知向量的模和夹角时,可利用定义法求解,即a·b=|a|·|b|cos
(2)当已知向量的坐标时,可利用坐标法求解,即若a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2.
运用两向量的数量积解决长度、夹角、垂直等问题,解题时应灵活选择相应公式求解.
题组训练三 平面向量的平行与垂直?
1.已知A(-2,1),B(6,-3),C(0,5),则△ABC的形状是
( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
【解析】选A.因为
=(8,-4),
=(2,4),
所以
·
=8×2+(-4)×4=0,
所以
⊥
,所以∠BAC=90°,
故△ABC是直角三角形.
2.已知向量
与
的夹角为120°,且|
|=3,|
|=2.若
且
则实数λ的值为________.?
【解析】由
知
=0,
即
=(λ
)·(
)
=(λ-1)
=(λ-1)×3×2×
-λ×9+4=0,解得λ=
.
答案:
【方法技巧】
1.证明共线问题常用的方法
(1)向量a,b(a≠0)共线?存在唯一实数λ,使b=λa.
(2)向量a=(x1,y1),b=(x2,y2)共线?x1y2-x2y1=0.
(3)向量a与b共线?存在不全为零的实数λ1,λ2,使λ1a+λ2b=0.
2.证明平面向量垂直问题的常用方法
a⊥b?a·b=0?x1x2+y1y2=0,
其中a=(x1,y1),b=(x2,y2),且a,b为非零向量.
题组训练四 平面向量的模、夹角?
1.设|a|=|b|=1,|3a-2b|=3,则|3a+b|的值为________.?
【解析】方法一:因为|3a-2b|=3,
所以9a2-12a·b+4b2=9.
又因为|a|=|b|=1,所以a·b=
.
所以|3a+b|2=(3a+b)2
=9a2+6a·b+b2
=9+6×
+1=12.
所以|3a+b|=2
.
方法二:设a=(x1,y1),b=(x2,y2).
因为|a|=|b|=1,
所以
因为3a-2b=(3x1-2x2,3y1-2y2),
所以|3a-2b|=
所以x1x2+y1y2=
.
所以|3a+b|=
答案:2
2.已知平面内三点A(1,0),B(0,1),C(2,5),求:
(1)|2
|.
(2)
与
夹角的余弦值.
(3)与
垂直的单位向量的坐标.
【解析】(1)由题意可得,
=(-1,1),
=(1,5),
所以2
=(-1,7),
所以|2
|=
(2)设
与
的夹角为θ,
则cos
θ=
(3)设与
垂直的单位向量的坐标为(x,y),因为
·(x,y)=(2,4)·(x,y)
=2x+4y=0,且x2+y2=1,
所以要求的向量的坐标为
【方法技巧】
1.夹角问题
求向量a,b夹角θ的步骤:
(1)求|a|,|b|,a·b;
(2)求cos
θ=
(夹角公式);
(3)结合θ的范围[0,π]确定θ的大小.因此求向量的夹角先转化为求向量夹
角的余弦值,再结合夹角的范围确定夹角的大小.
2.有关向量的模长问题
(1)若a=(x,y),则|a|2=x2+y2,或|a|=
(2)若向量a无坐标,则利用平方法,即|a|2=a2;
|a±b|2=a2±2a·b+b2.
题组训练五 平面向量在几何和物理方面的应用?
1.点P在平面上做匀速直线运动,速度v=(4,-3),设开始时点P的坐标为(-10,10),则5秒后点P的坐标为(速度单位:m/s,长度单位:m)( )
A.(-2,4)
B.(-30,25)
C.(10,-5)
D.(5,-10)
【解析】选C.5秒后点P的坐标为(-10,10)+5(4,-3)=(10,-5).
2.如图所示,P是正方形ABCD的对角线BD上一点,四边形PECF是矩形,求证:
(1)PA=EF.
(2)PA⊥EF.
【证明】(1)建立如图所示的平面直角坐标系,设正方形的边长为1,|
|=λ,
则A(0,1),
因为
所以
故PA=EF.
(2)因为
故PA⊥EF.
【方法技巧】
(1)向量的加减运算遵循平行四边形法则或三角形法则,数乘运算和线段平行之间、数量积运算和垂直、夹角、距离问题之间联系密切,因此用向量方法可以解决平面几何中的相关问题.
(2)利用平面向量解决几何问题的关键是恰当地引入向量,通过向量运算,解释几何性质.
(3)物理应用:速度、位移、力、功.
