上海市实验高中2020-2021学年高一下学期期中考试数学试题 Word版含答案
文档属性
| 名称 | 上海市实验高中2020-2021学年高一下学期期中考试数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-23 15:53:07 | ||
图片预览



文档简介
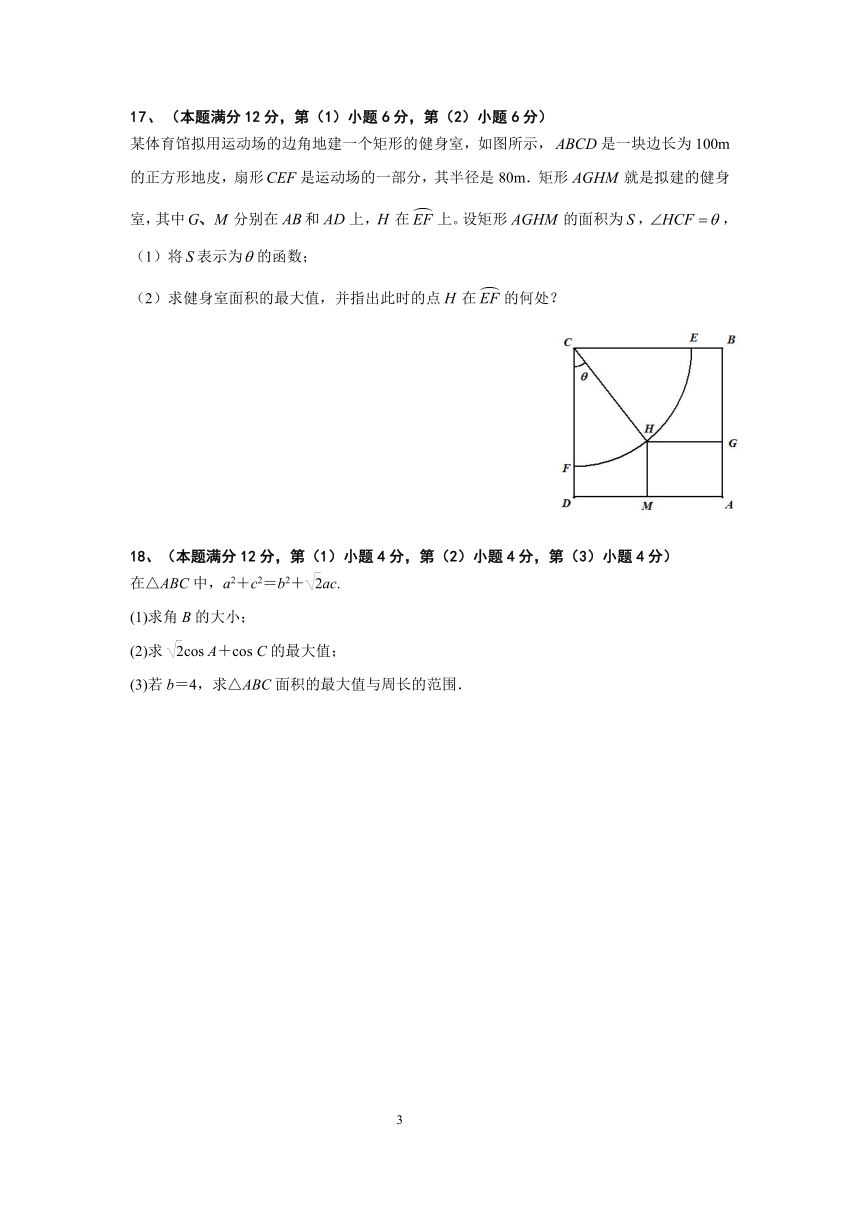
上海市实验学校2020-2021学年度第二学期期中考试
高一年级 数学试卷
填空题(本大题满分40分,共有10题,只要求直接填写结果,每题填对得4分,否则一律得零分)
1.终边在轴上的角的全体用集合表示是 .
2.已知扇形的弧长和半径都是,则扇形的面积是 .
3.已知角的终边落在函数的图象上,则 .
4.可以写成的形式,其中,则 .
5.在中,已知,则角A 的正弦值为 .
6.已知. 则的值为 .
7.已知函数,其中. 在一个周期内,当时,函数取得最大值;当时,函数取得最小值. 该函数的解析式为 .
8.已知函数既存在最大值,又存在最小值,则的值
为 .
9.如图所示,在中,,AC=6,BC=8,D为AC的中点,点E在BC上,分别连接BD、AE,交点为F,若,则CE= .
10.若,则函数的值域为 .
二、选择题(本大题满分16分,共有4题,每题都给出四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,否则一律得零分。)
11.如果,那么的值恒等于 ( )
(A). (B). (C). (D).
12. 的一个充要条件是 ( )
(A). (B). (C). (D).
13.函数 ( )
(A)是奇函数,也是周期函数. (B)是奇函数,不是周期函数.
(C)是偶函数,也是周期函数.(D)是偶函数,不是周期函数.
14.设函数,其中,已知在区间内有且只有4个零点,则下列的值中满足条件的是 ( )
(A) (B) (C) (D)
三、解答题(本大题满分44分,共有4题,解答下列各题必须写出必要的步骤)
15、(本题满分10分)
已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边过点P.
①求sinα的值;
②若角β满足sin(α+β)=,求cos β的值.
16、(本题满分10分)
求函数的定义域、值域及单调增区间.
17、(本题满分12分,第(1)小题6分,第(2)小题6分)
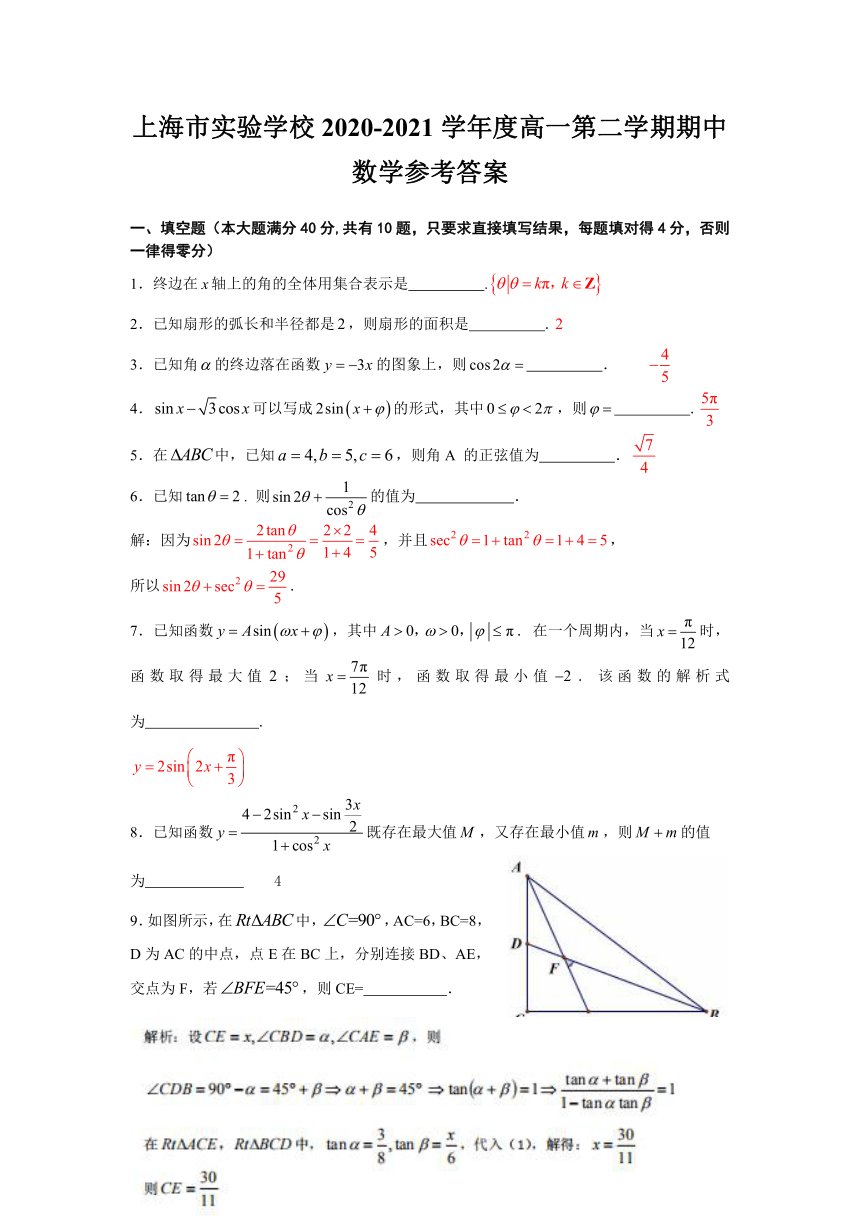
某体育馆拟用运动场的边角地建一个矩形的健身室,如图所示,是一块边长为100m的正方形地皮,扇形是运动场的一部分,其半径是80m.矩形就是拟建的健身室,其中分别在和上,在上。设矩形的面积为,,
(1)将表示为的函数;
(2)求健身室面积的最大值,并指出此时的点在的何处?
18、(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分)
在△ABC中,a2+c2=b2+ac.
(1)求角B的大小;
(2)求cos A+cos C的最大值;
(3)若b=4,求△ABC面积的最大值与周长的范围.
四、附加题
19、(本题满分10分)
设x≥y≥z≥,且x+y+z=,求乘积cosx siny cosz的最大值和最小值.
20、(本题满分10分)
求实数a的取值范围,使得对任意实数x和任意θ∈[0,],
恒有(x+3+2sinθcosθ)2+(x+asinθ+acosθ)2≥.
上海市实验学校2020-2021学年度高一第二学期期中数学参考答案
一、填空题(本大题满分40分,共有10题,只要求直接填写结果,每题填对得4分,否则一律得零分)
1.终边在轴上的角的全体用集合表示是 .
2.已知扇形的弧长和半径都是,则扇形的面积是 .
3.已知角的终边落在函数的图象上,则 .
4.可以写成的形式,其中,则 .
5.在中,已知,则角A 的正弦值为 .
6.已知. 则的值为 .
解:因为,并且,
所以.
7.已知函数,其中. 在一个周期内,当时,函数取得最大值;当时,函数取得最小值. 该函数的解析式为 .
8.已知函数既存在最大值,又存在最小值,则的值
为 4
9.如图所示,在中,,AC=6,BC=8,D为AC的中点,点E在BC上,分别连接BD、AE,交点为F,若,则CE= .
10.若,则函数的值域为 .
解:是奇函数,则求出最大值即可知最小值
令,则
,当时,k>0,此时
从而,所以函数的值域为
二、选择题(本大题满分16分,共有4题,每题都给出四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,否则一律得零分。)
11.如果,那么的值恒等于 ( C )
(A). (B). (C). (D).
12. 的一个充要条件是 ( A )
(A). (B). (C). (D).
13.函数( D )
(A)是奇函数,也是周期函数. (B)是奇函数,不是周期函数.
(C)是偶函数,也是周期函数.(D)是偶函数,不是周期函数.
14.设函数,其中,已知在区间内有且只有4个零点,则下列的值中满足条件的是( )
A. B. C. D.
三、解答题(本大题满分44分,共有4题,解答下列各题必须写出必要的步骤)
15.已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边过点P.
①求sinα的值;
②若角β满足sin(α+β)=,求cos β的值.
解:①由角α的终边过点P得sin α=-,
②由角α的终边过点P得cos α=-,
由sin(α+β)=得cos(α+β)=±.
由β=(α+β)-α得cos β=cos(α+β)cos α+sin(α+β)sin α,
所以cos β=-或cos β=.
16.求函数的定义域、值域及单调增区间.
解:由得已知函数的定义域为.
已知函数可化为.
因为,所以.
此时,. 所以,已知函数的值域为.
单调增区间为:
17.某体育馆拟用运动场的边角地建一个矩形的健身室,如图所示,是一块边长为100m的正方形地皮,扇形是运动场的一部分,其半径是80m.矩形就是拟建的健身室,其中分别在和上,在上。设矩形的面积为,,
(1)将表示为的函数;(5分)
(2)求健身室面积的最大值,并指出此时的点在的何处?
解:
(1)延长交于,,
整理得:
(2)设, 则,
当时,,
此时,,
当在的端点或处时,健身室面积最大,最大面积为2000平方米.
18.在△ABC中,a2+c2=b2+ac.
(1)求角B的大小;
(2)求cos A+cos C的最大值;
(3)若b=4,求△ABC面积的最大值与周长的范围.
【解】 (1)由余弦定理及题设得
cos B===. 又0(2)由(1)知A+C=,则
cos A+cos C=cos A+cos=cos A-cos A+sin A
=cos A+sin A=cos.
因为0(3)由题意知
a2+c2-ac=16,由基本不等式得16≥(2-)ac.
所以ac≤=8(2+),当且仅当a=c=2时取等号.
所以S△ABC=acsin B≤×8(2+)×=4(+1),
即当a=c=2时,S△ABC的最大值为4(+1).
又由a2+c2-ac=16,得(a+c)2-(2+)ac=16.
由均值不等式≥知ac≤(a+c)2,当且仅当a=c时取等号,
所以≤(a+c)2,
所以(a+c)2≤32(2+),
所以a+c≤4,
当且仅当a=c=2时,取等号.
又a+c>b=4,所以a+b+c>2b,
所以8四、附加题:
19.设x≥y≥z≥,且x+y+z=,求乘积cosx siny cosz的最大值和最小值.
解:由于x≥y≥z≥,故≤x≤-×2=.
∴ cosx siny cosz=cosx×[sin(y+z)+sin(y-z)]=cos2x+cosxsin(y-z)≥cos2=.即最小值.
(由于≤x≤,y≥z,故cosxsin(y-z)≥0),当y=z=,x=时,cosx siny cosz=.
∵ cosx siny cosz=cosz×[sin(x+y)-sin(x-y)]=cos2z-coszsin(x-y).
由于sin(x-y)≥0,cosz>0,故cosx siny cosz≤cos2z=cos2=(1+cos)=.
当x= y=,z=时取得最大值. ∴ 最大值,最小值.
20.求实数a的取值范围,使得对任意实数x和任意θ∈[0,],恒有
(x+3+2sinθcosθ)2+(x+asinθ+acosθ)2≥.
解:令sinθ+cosθ=u,则2sinθcosθ=u2-1,当θ∈[0,]时,u∈[1,].
并记f(x)= (x+3+2sinθcosθ)2+(x+asinθ+acosθ)2.
∴ f(x)=(x+2+u2)2+(x+au)2=2x2+2(u2+au+2)x+(u2+2)2+(au)2
=2[x+(u2+au+2)]2+(u2-au+2)2.
∴ x=-(u2+au+2)时,f(x)取得最小值(u2-au+2)2.
∴ u2-au+2≥,或u2-au+2≤-.
∴ a≤u+,或a≥u+.当u∈[1,]时,u+∈[,];u+∈[,].
∴ a≤或a≥.
10
高一年级 数学试卷
填空题(本大题满分40分,共有10题,只要求直接填写结果,每题填对得4分,否则一律得零分)
1.终边在轴上的角的全体用集合表示是 .
2.已知扇形的弧长和半径都是,则扇形的面积是 .
3.已知角的终边落在函数的图象上,则 .
4.可以写成的形式,其中,则 .
5.在中,已知,则角A 的正弦值为 .
6.已知. 则的值为 .
7.已知函数,其中. 在一个周期内,当时,函数取得最大值;当时,函数取得最小值. 该函数的解析式为 .
8.已知函数既存在最大值,又存在最小值,则的值
为 .
9.如图所示,在中,,AC=6,BC=8,D为AC的中点,点E在BC上,分别连接BD、AE,交点为F,若,则CE= .
10.若,则函数的值域为 .
二、选择题(本大题满分16分,共有4题,每题都给出四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,否则一律得零分。)
11.如果,那么的值恒等于 ( )
(A). (B). (C). (D).
12. 的一个充要条件是 ( )
(A). (B). (C). (D).
13.函数 ( )
(A)是奇函数,也是周期函数. (B)是奇函数,不是周期函数.
(C)是偶函数,也是周期函数.(D)是偶函数,不是周期函数.
14.设函数,其中,已知在区间内有且只有4个零点,则下列的值中满足条件的是 ( )
(A) (B) (C) (D)
三、解答题(本大题满分44分,共有4题,解答下列各题必须写出必要的步骤)
15、(本题满分10分)
已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边过点P.
①求sinα的值;
②若角β满足sin(α+β)=,求cos β的值.
16、(本题满分10分)
求函数的定义域、值域及单调增区间.
17、(本题满分12分,第(1)小题6分,第(2)小题6分)
某体育馆拟用运动场的边角地建一个矩形的健身室,如图所示,是一块边长为100m的正方形地皮,扇形是运动场的一部分,其半径是80m.矩形就是拟建的健身室,其中分别在和上,在上。设矩形的面积为,,
(1)将表示为的函数;
(2)求健身室面积的最大值,并指出此时的点在的何处?
18、(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分)
在△ABC中,a2+c2=b2+ac.
(1)求角B的大小;
(2)求cos A+cos C的最大值;
(3)若b=4,求△ABC面积的最大值与周长的范围.
四、附加题
19、(本题满分10分)
设x≥y≥z≥,且x+y+z=,求乘积cosx siny cosz的最大值和最小值.
20、(本题满分10分)
求实数a的取值范围,使得对任意实数x和任意θ∈[0,],
恒有(x+3+2sinθcosθ)2+(x+asinθ+acosθ)2≥.
上海市实验学校2020-2021学年度高一第二学期期中数学参考答案
一、填空题(本大题满分40分,共有10题,只要求直接填写结果,每题填对得4分,否则一律得零分)
1.终边在轴上的角的全体用集合表示是 .
2.已知扇形的弧长和半径都是,则扇形的面积是 .
3.已知角的终边落在函数的图象上,则 .
4.可以写成的形式,其中,则 .
5.在中,已知,则角A 的正弦值为 .
6.已知. 则的值为 .
解:因为,并且,
所以.
7.已知函数,其中. 在一个周期内,当时,函数取得最大值;当时,函数取得最小值. 该函数的解析式为 .
8.已知函数既存在最大值,又存在最小值,则的值
为 4
9.如图所示,在中,,AC=6,BC=8,D为AC的中点,点E在BC上,分别连接BD、AE,交点为F,若,则CE= .
10.若,则函数的值域为 .
解:是奇函数,则求出最大值即可知最小值
令,则
,当时,k>0,此时
从而,所以函数的值域为
二、选择题(本大题满分16分,共有4题,每题都给出四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,否则一律得零分。)
11.如果,那么的值恒等于 ( C )
(A). (B). (C). (D).
12. 的一个充要条件是 ( A )
(A). (B). (C). (D).
13.函数( D )
(A)是奇函数,也是周期函数. (B)是奇函数,不是周期函数.
(C)是偶函数,也是周期函数.(D)是偶函数,不是周期函数.
14.设函数,其中,已知在区间内有且只有4个零点,则下列的值中满足条件的是( )
A. B. C. D.
三、解答题(本大题满分44分,共有4题,解答下列各题必须写出必要的步骤)
15.已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边过点P.
①求sinα的值;
②若角β满足sin(α+β)=,求cos β的值.
解:①由角α的终边过点P得sin α=-,
②由角α的终边过点P得cos α=-,
由sin(α+β)=得cos(α+β)=±.
由β=(α+β)-α得cos β=cos(α+β)cos α+sin(α+β)sin α,
所以cos β=-或cos β=.
16.求函数的定义域、值域及单调增区间.
解:由得已知函数的定义域为.
已知函数可化为.
因为,所以.
此时,. 所以,已知函数的值域为.
单调增区间为:
17.某体育馆拟用运动场的边角地建一个矩形的健身室,如图所示,是一块边长为100m的正方形地皮,扇形是运动场的一部分,其半径是80m.矩形就是拟建的健身室,其中分别在和上,在上。设矩形的面积为,,
(1)将表示为的函数;(5分)
(2)求健身室面积的最大值,并指出此时的点在的何处?
解:
(1)延长交于,,
整理得:
(2)设, 则,
当时,,
此时,,
当在的端点或处时,健身室面积最大,最大面积为2000平方米.
18.在△ABC中,a2+c2=b2+ac.
(1)求角B的大小;
(2)求cos A+cos C的最大值;
(3)若b=4,求△ABC面积的最大值与周长的范围.
【解】 (1)由余弦定理及题设得
cos B===. 又0
cos A+cos C=cos A+cos=cos A-cos A+sin A
=cos A+sin A=cos.
因为0
a2+c2-ac=16,由基本不等式得16≥(2-)ac.
所以ac≤=8(2+),当且仅当a=c=2时取等号.
所以S△ABC=acsin B≤×8(2+)×=4(+1),
即当a=c=2时,S△ABC的最大值为4(+1).
又由a2+c2-ac=16,得(a+c)2-(2+)ac=16.
由均值不等式≥知ac≤(a+c)2,当且仅当a=c时取等号,
所以≤(a+c)2,
所以(a+c)2≤32(2+),
所以a+c≤4,
当且仅当a=c=2时,取等号.
又a+c>b=4,所以a+b+c>2b,
所以8
19.设x≥y≥z≥,且x+y+z=,求乘积cosx siny cosz的最大值和最小值.
解:由于x≥y≥z≥,故≤x≤-×2=.
∴ cosx siny cosz=cosx×[sin(y+z)+sin(y-z)]=cos2x+cosxsin(y-z)≥cos2=.即最小值.
(由于≤x≤,y≥z,故cosxsin(y-z)≥0),当y=z=,x=时,cosx siny cosz=.
∵ cosx siny cosz=cosz×[sin(x+y)-sin(x-y)]=cos2z-coszsin(x-y).
由于sin(x-y)≥0,cosz>0,故cosx siny cosz≤cos2z=cos2=(1+cos)=.
当x= y=,z=时取得最大值. ∴ 最大值,最小值.
20.求实数a的取值范围,使得对任意实数x和任意θ∈[0,],恒有
(x+3+2sinθcosθ)2+(x+asinθ+acosθ)2≥.
解:令sinθ+cosθ=u,则2sinθcosθ=u2-1,当θ∈[0,]时,u∈[1,].
并记f(x)= (x+3+2sinθcosθ)2+(x+asinθ+acosθ)2.
∴ f(x)=(x+2+u2)2+(x+au)2=2x2+2(u2+au+2)x+(u2+2)2+(au)2
=2[x+(u2+au+2)]2+(u2-au+2)2.
∴ x=-(u2+au+2)时,f(x)取得最小值(u2-au+2)2.
∴ u2-au+2≥,或u2-au+2≤-.
∴ a≤u+,或a≥u+.当u∈[1,]时,u+∈[,];u+∈[,].
∴ a≤或a≥.
10
同课章节目录
