勾股定理学案(3节)
图片预览


文档简介
勾股定理(1)学案
教学目标
1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2.培养在实际生活中发现问题总结规律的意识和能力。
重点:勾股定理的内容及证明。难点:勾股定理的证明。
学习过程:
一.探究新知
1 以等腰直角三角形两直角边为边长的小正方形的面积和以斜边为边长的大正方形的面积之间有什么关系?
A的面积 B的面积 C的面积
图1-1
图1-2
A、B、C三个正方形的面积关系结论:
2.那么一般的直角三角形是否也有这样的特点呢?
填表:
A的面积 B的面积 C的面积
图1-3
图1-4
A、B、C三个正方形的面积关系结论:
。
3、对于任意的直角三角形也有这个性质吗?
由上面的几个例子我们猜想:
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 + =
4、利用面积相等证明猜想
已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。求证:a2+b2=c2。
证明一:如图所示
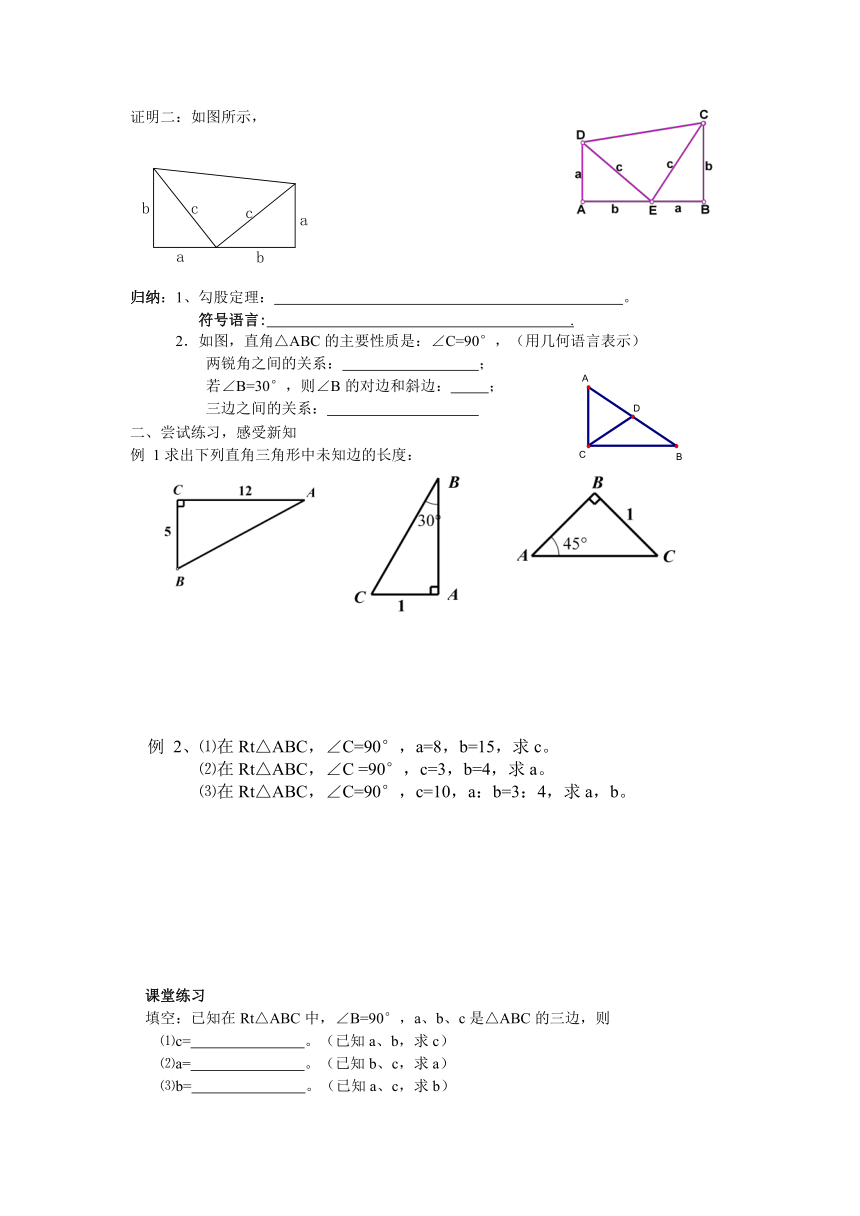
证明二:如图所示,
归纳:1、勾股定理: 。
符号语言: .
2.如图,直角△ABC的主要性质是:∠C=90°,(用几何语言表示)
两锐角之间的关系: ;
若∠B=30°,则∠B的对边和斜边: ;
三边之间的关系:
二、尝试练习,感受新知
例 1求出下列直角三角形中未知边的长度:
例 2、⑴在Rt△ABC,∠C=90°,a=8,b=15,求c。
⑵在Rt△ABC,∠C =90°,c=3,b=4,求a。
⑶在Rt△ABC,∠C=90°,c=10,a:b=3:4,求a,b。
课堂练习
填空:已知在Rt△ABC中,∠B=90°,a、b、c是△ABC的三边,则
⑴c= 。(已知a、b,求c)
⑵a= 。(已知b、c,求a)
⑶b= 。(已知a、c,求b)
18.1 勾股定理(2)学案
教学目标1.会用勾股定理解决简单的实际问题。2.树立数形结合的思想。
能利用勾股定理,根据已知直角三角形的两边长求第三条边长;并在数轴上表示无理数。
2、体会数与形的密切联系,增强应用意识,提高运用勾股定理解决问题的能力。
复习
勾股定理内容: 。
符号语言及变形: 。
应用举例
在Rt△ABC,∠C=90°
⑴已知a=b=5,求c。
⑵已知a:b=1:2,c=5, 求a。
⑶已知b=15,∠A=30°,求a,c。
⑷已知两边长分别为5和12,求第三边。
已知:如图,在△ABC中,AD是BC边上的高,∠C=60°,AB=,AC=4,求BC的长。
已知:如图,△ABC中,AC=4,∠A =45°,∠B=60°,求线段BC的长。
已知:如图,△ABC中,AB=15, BC=14,AC=13,求△ABC的面积
课堂练习
1 .△ABC中,AB=10,∠C=90°∠A=30°,则AC= 。
2、三角形两直角边长分别为4、6,则斜边上的高为 。
3、已知:如图,四边形ABCD中,AD∥BC,AD⊥DC, AB⊥AC,∠B=60°,
CD=1cm,求BC的长。
4.已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=,
求(1)AB的长;(2)S△ABC。
18.1 勾股定理(3)学案
教学目标1.会用勾股定理解决简单的实际问题。
2.树立数形结合的思想。
例习题分析
例1:一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
例2如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
例3、有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少 (π的值取3)
练习:
1.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是 米。
2.如图,山坡上两株树木之间的坡面距离是4米,则这两株树之间的垂直距离是
米,水平距离是 米。
3、一棵树高8米,如图,在B点处折断,树顶距树根4米远,折断处离地面有 米。
2题图 3题图 4题图
4、如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 m。
思考.已知长方体的长为2cm、宽为1cm、高为4cm,一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是多少
1.探究:我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?
2.分析:如果能画出长为_______的线段,就能在数轴上画出表示的点。容易知道,长为的线段是两条直角边都为______的直角边的斜边。长为的线段能是直角边为正整数的直角三角形的斜边吗?
利用勾股定理,可以发现,长为的线段是直角边为正整数_____、 ______的直角三角形的斜边。
3.作法:在数轴上找到点A,使OA=_____,作直线垂直于OA,在上取点B,使AB=_____,以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示的点。
4.在数轴上画出表示的点?(尺规作图)
下面就请同学们在数轴上画出表示的点.
生:步骤如下:
1.在数轴上找到点A,使OA=3;
2.作直线L垂直于OA,在L上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交于点C,则点C即为表示的点.
活动3
练习:在数轴上作出表示的点.
A
B
C
A
B
C
图1-1
图1-2
A
B
C
图1-3
A
B
C
图1-4
B
A
B
A
C
Dˊ
A
B
C
D
Aˊ
Bˊ
Cˊ
教学目标
1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2.培养在实际生活中发现问题总结规律的意识和能力。
重点:勾股定理的内容及证明。难点:勾股定理的证明。
学习过程:
一.探究新知
1 以等腰直角三角形两直角边为边长的小正方形的面积和以斜边为边长的大正方形的面积之间有什么关系?
A的面积 B的面积 C的面积
图1-1
图1-2
A、B、C三个正方形的面积关系结论:
2.那么一般的直角三角形是否也有这样的特点呢?
填表:
A的面积 B的面积 C的面积
图1-3
图1-4
A、B、C三个正方形的面积关系结论:
。
3、对于任意的直角三角形也有这个性质吗?
由上面的几个例子我们猜想:
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 + =
4、利用面积相等证明猜想
已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。求证:a2+b2=c2。
证明一:如图所示
证明二:如图所示,
归纳:1、勾股定理: 。
符号语言: .
2.如图,直角△ABC的主要性质是:∠C=90°,(用几何语言表示)
两锐角之间的关系: ;
若∠B=30°,则∠B的对边和斜边: ;
三边之间的关系:
二、尝试练习,感受新知
例 1求出下列直角三角形中未知边的长度:
例 2、⑴在Rt△ABC,∠C=90°,a=8,b=15,求c。
⑵在Rt△ABC,∠C =90°,c=3,b=4,求a。
⑶在Rt△ABC,∠C=90°,c=10,a:b=3:4,求a,b。
课堂练习
填空:已知在Rt△ABC中,∠B=90°,a、b、c是△ABC的三边,则
⑴c= 。(已知a、b,求c)
⑵a= 。(已知b、c,求a)
⑶b= 。(已知a、c,求b)
18.1 勾股定理(2)学案
教学目标1.会用勾股定理解决简单的实际问题。2.树立数形结合的思想。
能利用勾股定理,根据已知直角三角形的两边长求第三条边长;并在数轴上表示无理数。
2、体会数与形的密切联系,增强应用意识,提高运用勾股定理解决问题的能力。
复习
勾股定理内容: 。
符号语言及变形: 。
应用举例
在Rt△ABC,∠C=90°
⑴已知a=b=5,求c。
⑵已知a:b=1:2,c=5, 求a。
⑶已知b=15,∠A=30°,求a,c。
⑷已知两边长分别为5和12,求第三边。
已知:如图,在△ABC中,AD是BC边上的高,∠C=60°,AB=,AC=4,求BC的长。
已知:如图,△ABC中,AC=4,∠A =45°,∠B=60°,求线段BC的长。
已知:如图,△ABC中,AB=15, BC=14,AC=13,求△ABC的面积
课堂练习
1 .△ABC中,AB=10,∠C=90°∠A=30°,则AC= 。
2、三角形两直角边长分别为4、6,则斜边上的高为 。
3、已知:如图,四边形ABCD中,AD∥BC,AD⊥DC, AB⊥AC,∠B=60°,
CD=1cm,求BC的长。
4.已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=,
求(1)AB的长;(2)S△ABC。
18.1 勾股定理(3)学案
教学目标1.会用勾股定理解决简单的实际问题。
2.树立数形结合的思想。
例习题分析
例1:一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
例2如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
例3、有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少 (π的值取3)
练习:
1.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是 米。
2.如图,山坡上两株树木之间的坡面距离是4米,则这两株树之间的垂直距离是
米,水平距离是 米。
3、一棵树高8米,如图,在B点处折断,树顶距树根4米远,折断处离地面有 米。
2题图 3题图 4题图
4、如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 m。
思考.已知长方体的长为2cm、宽为1cm、高为4cm,一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是多少
1.探究:我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?
2.分析:如果能画出长为_______的线段,就能在数轴上画出表示的点。容易知道,长为的线段是两条直角边都为______的直角边的斜边。长为的线段能是直角边为正整数的直角三角形的斜边吗?
利用勾股定理,可以发现,长为的线段是直角边为正整数_____、 ______的直角三角形的斜边。
3.作法:在数轴上找到点A,使OA=_____,作直线垂直于OA,在上取点B,使AB=_____,以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示的点。
4.在数轴上画出表示的点?(尺规作图)
下面就请同学们在数轴上画出表示的点.
生:步骤如下:
1.在数轴上找到点A,使OA=3;
2.作直线L垂直于OA,在L上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交于点C,则点C即为表示的点.
活动3
练习:在数轴上作出表示的点.
A
B
C
A
B
C
图1-1
图1-2
A
B
C
图1-3
A
B
C
图1-4
B
A
B
A
C
Dˊ
A
B
C
D
Aˊ
Bˊ
Cˊ
