2020~2021学年八年级数学人教版下册第18章平行四边形练习试卷(Word版含答案)
文档属性
| 名称 | 2020~2021学年八年级数学人教版下册第18章平行四边形练习试卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 229.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-23 00:00:00 | ||
图片预览

文档简介
第18章检测卷
一、选择
1.下列图形中,是轴对称图形且对称轴最多的是( )
A.矩形 B.平行四边形 C.菱形 D.正方形
2.有下列说法:①四边相等的四边形一定是菱形;②顺次连接矩形各边中点形成的四边形一定是正方形;③对角线相等的四边形一定是矩形;④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分.其中正确的个数是( )
A.4 B.3 C.2 D.1
3.菱形的两条对角线长分别是6 cm和8 cm,则菱形的边长是( )
A.10 cm B.7 cm C.5 cm D.4 cm
4.在四边形ABCD中,对角线AC,BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
5.如图,在△ABC中,AB=AC=5,D是BC上一点,DE∥AB,交AC于点E,DF∥AC,交AB于点F,则四边形AFDE的周长是( )
A.5 B.10 C.15 D.20
6.如图,在□ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G, ∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE.下列结论错误的是( )
A.BO=OH B.DF=CE C.DH=CG D.AB=AE
7.如图,在菱形ABCD中,∠A=110°,E,F分别是边AB,BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
A.35° B.45° C.50° D.55°
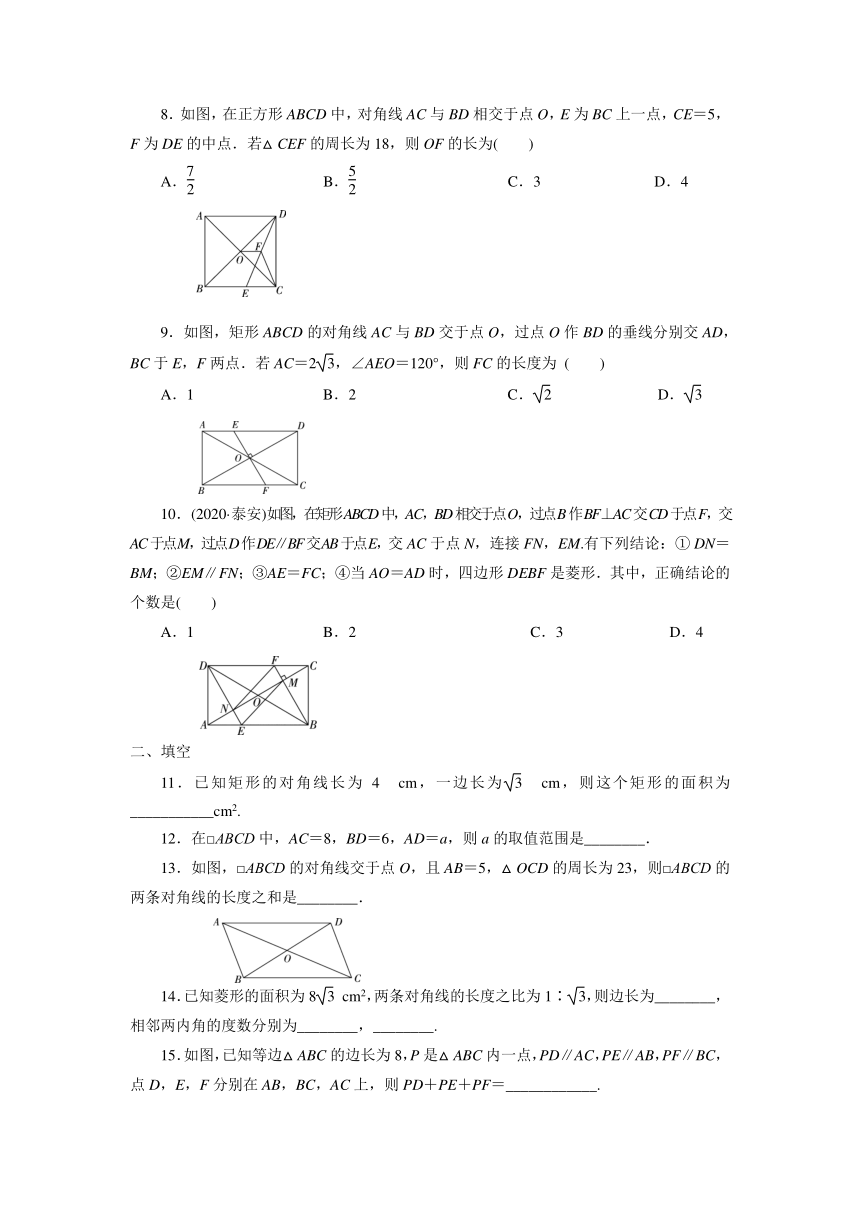
8.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为( )
A. B. C.3 D.4
9.如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2,∠AEO=120°,则FC的长度为 ( )
A.1 B.2 C. D.
10.(2020·泰安)如图,在矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD于点F,交AC于点M,过点D作DE∥BF交AB于点E,交AC于点N,连接FN,EM.有下列结论:① DN=BM;②EM∥FN;③AE=FC;④当AO=AD时,四边形DEBF是菱形.其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空
11.已知矩形的对角线长为4 cm,一边长为 cm,则这个矩形的面积为___________cm2.
12.在□ABCD中,AC=8,BD=6,AD=a,则a的取值范围是________.
13.如图,□ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则□ABCD的两条对角线的长度之和是________.
14.已知菱形的面积为8 cm2,两条对角线的长度之比为1∶,则边长为________,相邻两内角的度数分别为________,________.
15.如图,已知等边△ABC的边长为8,P是△ABC内一点,PD∥AC,PE∥AB,PF∥BC,点D,E,F分别在AB,BC,AC上,则PD+PE+PF=____________.
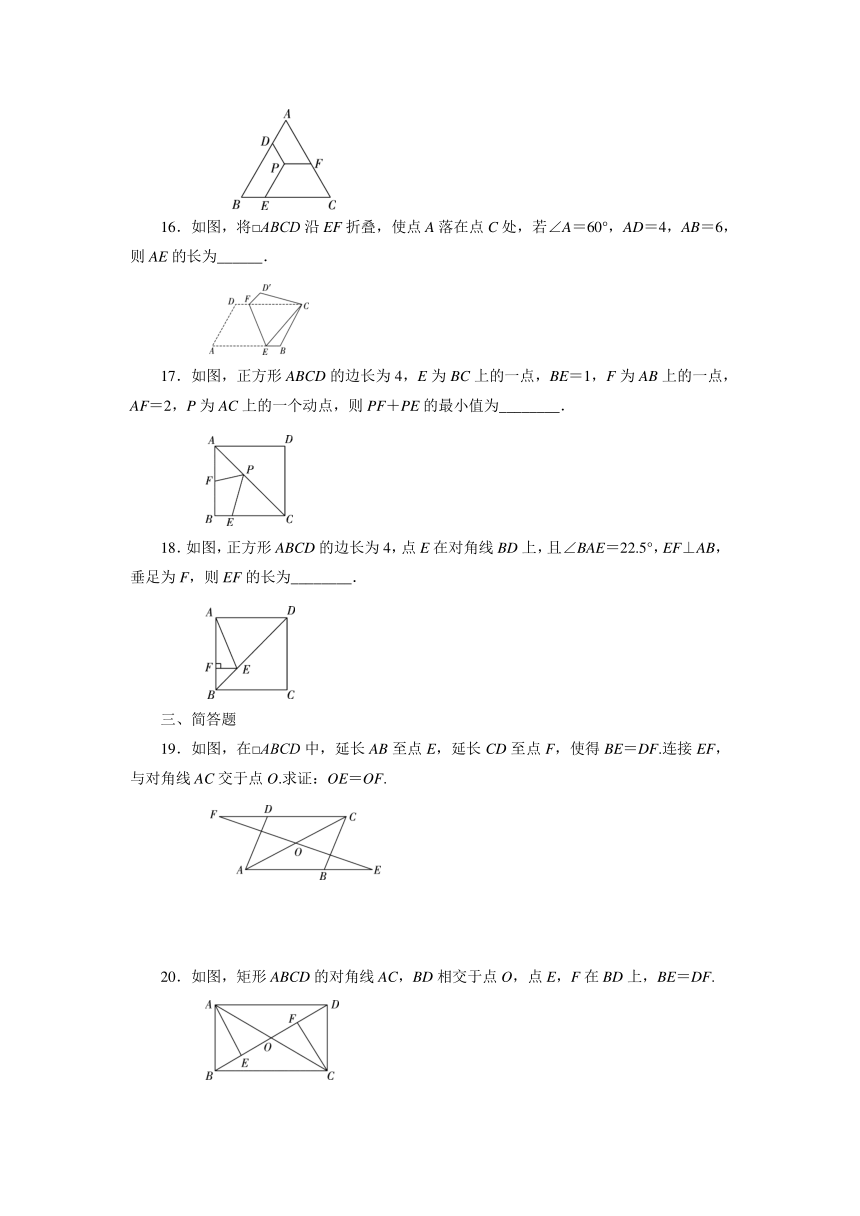
16.如图,将□ABCD沿EF折叠,使点A落在点C处,若∠A=60°,AD=4,AB=6,则AE的长为______.
17.如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上的一个动点,则PF+PE的最小值为________.
18.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为________.
三、简答题
19.如图,在□ABCD中,延长AB至点E,延长CD至点F,使得BE=DF.连接EF,与对角线AC交于点O.求证:OE=OF.
20.如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
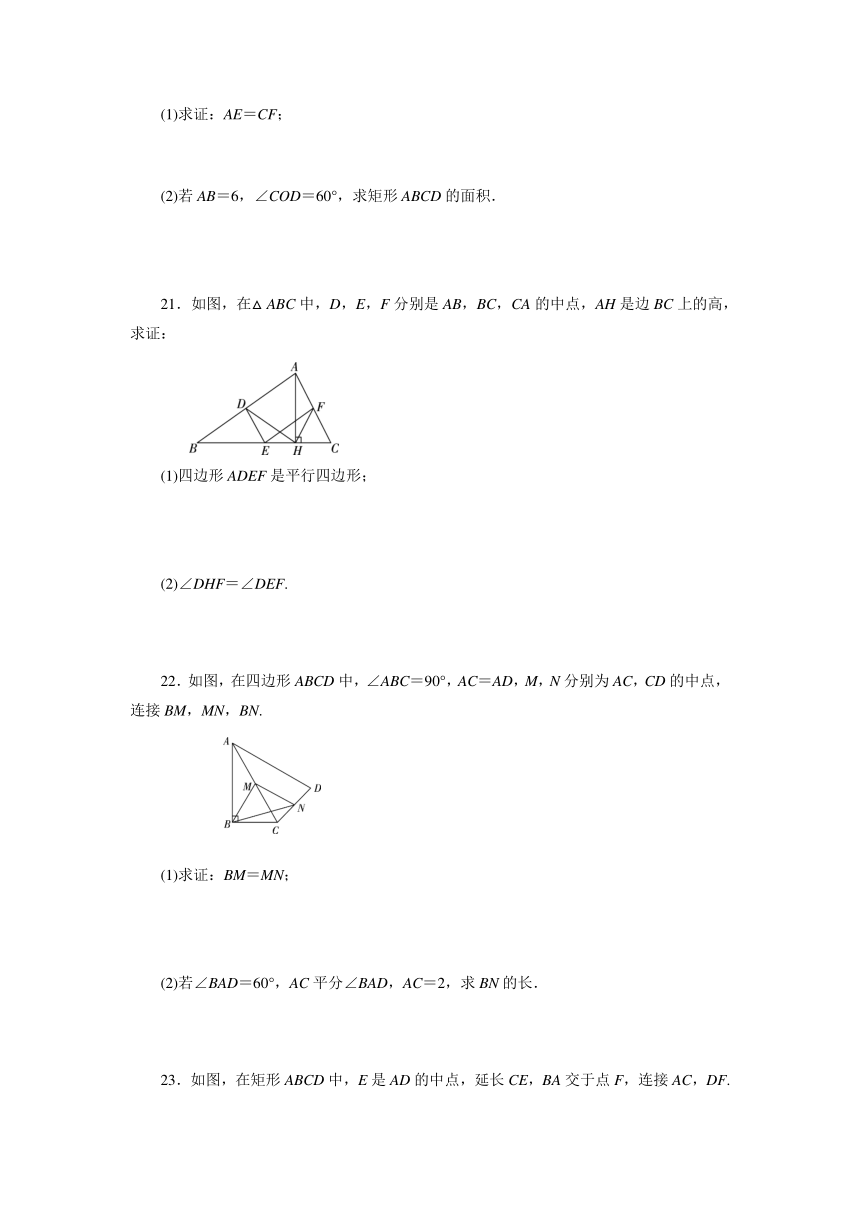
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.
21.如图,在△ABC中,D,E,F分别是AB,BC,CA的中点,AH是边BC上的高,求证:
(1)四边形ADEF是平行四边形;
(2)∠DHF=∠DEF.
22.如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)若∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
23.如图,在矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.
24.如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2,点H是BD上的一个动点,求HG+HC的最小值.
答案
1-5 DCDBB 6-10 DDAAD 11. 12. 1
4 cm 60° 120° 15. 8 16. 17. 18. 4-2
证明:连接AF,CE,∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC.
又∵BE=DF,∴AE=FC.
又∵AE∥CF,∴四边形AECF是平行四边形,∴OE=OF.
20.(1)证明:∵四边形ABCD是矩形,∴OA=OC,OB=OD.
∵BE=DF,∴OE=OF.
在△AOE和△COF中,
∴△AOE≌△COF,∴AE=CF.
(2)解:∵OA=OC,OB=OD,AC=BD,∴OA=OB.
∵∠AOB=∠COD=60°,∴△AOB是等边三角形,
∴OA=AB=6,∴AC=2OA=12.
在Rt△ABC中,BC==6,
∴矩形ABCD的面积为AB·BC=6×6=36.
21.(1)证明:∵D,E分别是AB,BC的中点,
∴DE∥AC,同理,得EF∥AB,
∴四边形ADEF是平行四边形.
(2)解:∵四边形ADEF是平行四边形,∴∠DAF=∠DEF.
∵在Rt△AHB中,D是AB的中点,∴DH=AB=AD,
∴∠DAH=∠DHA,同理,得∠FAH=∠FHA,
∴∠DAH+∠FAH=∠DHA+∠FHA,即∠DAF=∠DHF,
∴∠DHF=∠DEF.
22.(1)证明:在△CAD中,∵M,N分别是AC,CD的中点,
∴MN∥AD且MN=AD.
在Rt△ABC中,∵M是AC的中点,∠ABC=90°,
∴BM=AC.
∵AC=AD,∴MN=BM.
(2)解:∵∠BAD=60°且AC平分∠BAD,
∴∠BAC=∠DAC=30°.
由(1)知,BM=AC=AM=MC,
∴∠BAM=∠ABM,
∴∠BMC=∠BAM+∠ABM=2∠BAM=60°.
∵MN∥AD,∴∠NMC=∠DAC=30°,
∴∠BMN=∠BMC+∠NMC=90°,
∴BN2=BM2+MN2,而由(1)知,MN=BM=AC=×2=1,∴BN=.
23.(1)∵MN∥AD,∴∠NMC=∠DAC=30°,
∴∠BMN=∠BMC+∠NMC=90°,
∴BN2=BM2+MN2,而由(1)知,MN=BM=AC=×2=1,∴BN=.
(2)解:BC=2CD.理由如下:
因为CF平分∠BCD,所以∠DCE=45°.
因为∠CDE=90°,所以△CDE是等腰直角三角形,
所以CD=DE.
因为E是AD的中点,所以AD=2CD.
因为AD=BC,所以BC=2CD.
24.(1)解:四边形EBGD是菱形.理由:
∵EG垂直平分BD,
∴DF=BF,EB=ED,GB=GD,∴∠EBD=∠EDB.
∵BD是△ABC的角平分线,
∴∠EBD=∠DBC,∴∠EDF=∠GBF.
在△EFD和△GFB中,
∴△EFD≌△GFB,∴ED=BG,∴BE=ED=DG=GB,
∴四边形EBGD是菱形.
(2)解:如答图,连接EC交BD于点H,连接HG,此时HG+HC最小,作EM⊥BC于点M,DN⊥BC于点N.
在Rt△EBM中,∵∠EMB=90°,∠EBM=30°,EB=ED=2,
∴EM=BE=.
由(1)知四边形EBGD是菱形,∴DE∥BC,
∵EM⊥BC,DN⊥BC,
∴EM∥DN,EM=DN=,MN=DE=2.
在Rt△DNC中,∵∠DNC=90°,∠DCN=45°,
∴∠NDC=∠NCD=45°,
∴DN=NC=,∴MC=3.
在Rt△EMC中,∵∠EMC=90°,EM=,MC=3,
∴EC===10.
∵HG+HC=EH+HC=EC,∴HG+HC的最小值为10.
一、选择
1.下列图形中,是轴对称图形且对称轴最多的是( )
A.矩形 B.平行四边形 C.菱形 D.正方形
2.有下列说法:①四边相等的四边形一定是菱形;②顺次连接矩形各边中点形成的四边形一定是正方形;③对角线相等的四边形一定是矩形;④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分.其中正确的个数是( )
A.4 B.3 C.2 D.1
3.菱形的两条对角线长分别是6 cm和8 cm,则菱形的边长是( )
A.10 cm B.7 cm C.5 cm D.4 cm
4.在四边形ABCD中,对角线AC,BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
5.如图,在△ABC中,AB=AC=5,D是BC上一点,DE∥AB,交AC于点E,DF∥AC,交AB于点F,则四边形AFDE的周长是( )
A.5 B.10 C.15 D.20
6.如图,在□ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G, ∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE.下列结论错误的是( )
A.BO=OH B.DF=CE C.DH=CG D.AB=AE
7.如图,在菱形ABCD中,∠A=110°,E,F分别是边AB,BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
A.35° B.45° C.50° D.55°
8.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为( )
A. B. C.3 D.4
9.如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2,∠AEO=120°,则FC的长度为 ( )
A.1 B.2 C. D.
10.(2020·泰安)如图,在矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD于点F,交AC于点M,过点D作DE∥BF交AB于点E,交AC于点N,连接FN,EM.有下列结论:① DN=BM;②EM∥FN;③AE=FC;④当AO=AD时,四边形DEBF是菱形.其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空
11.已知矩形的对角线长为4 cm,一边长为 cm,则这个矩形的面积为___________cm2.
12.在□ABCD中,AC=8,BD=6,AD=a,则a的取值范围是________.
13.如图,□ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则□ABCD的两条对角线的长度之和是________.
14.已知菱形的面积为8 cm2,两条对角线的长度之比为1∶,则边长为________,相邻两内角的度数分别为________,________.
15.如图,已知等边△ABC的边长为8,P是△ABC内一点,PD∥AC,PE∥AB,PF∥BC,点D,E,F分别在AB,BC,AC上,则PD+PE+PF=____________.
16.如图,将□ABCD沿EF折叠,使点A落在点C处,若∠A=60°,AD=4,AB=6,则AE的长为______.
17.如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上的一个动点,则PF+PE的最小值为________.
18.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为________.
三、简答题
19.如图,在□ABCD中,延长AB至点E,延长CD至点F,使得BE=DF.连接EF,与对角线AC交于点O.求证:OE=OF.
20.如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.
21.如图,在△ABC中,D,E,F分别是AB,BC,CA的中点,AH是边BC上的高,求证:
(1)四边形ADEF是平行四边形;
(2)∠DHF=∠DEF.
22.如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)若∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
23.如图,在矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.
24.如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2,点H是BD上的一个动点,求HG+HC的最小值.
答案
1-5 DCDBB 6-10 DDAAD 11. 12. 1
4 cm 60° 120° 15. 8 16. 17. 18. 4-2
证明:连接AF,CE,∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC.
又∵BE=DF,∴AE=FC.
又∵AE∥CF,∴四边形AECF是平行四边形,∴OE=OF.
20.(1)证明:∵四边形ABCD是矩形,∴OA=OC,OB=OD.
∵BE=DF,∴OE=OF.
在△AOE和△COF中,
∴△AOE≌△COF,∴AE=CF.
(2)解:∵OA=OC,OB=OD,AC=BD,∴OA=OB.
∵∠AOB=∠COD=60°,∴△AOB是等边三角形,
∴OA=AB=6,∴AC=2OA=12.
在Rt△ABC中,BC==6,
∴矩形ABCD的面积为AB·BC=6×6=36.
21.(1)证明:∵D,E分别是AB,BC的中点,
∴DE∥AC,同理,得EF∥AB,
∴四边形ADEF是平行四边形.
(2)解:∵四边形ADEF是平行四边形,∴∠DAF=∠DEF.
∵在Rt△AHB中,D是AB的中点,∴DH=AB=AD,
∴∠DAH=∠DHA,同理,得∠FAH=∠FHA,
∴∠DAH+∠FAH=∠DHA+∠FHA,即∠DAF=∠DHF,
∴∠DHF=∠DEF.
22.(1)证明:在△CAD中,∵M,N分别是AC,CD的中点,
∴MN∥AD且MN=AD.
在Rt△ABC中,∵M是AC的中点,∠ABC=90°,
∴BM=AC.
∵AC=AD,∴MN=BM.
(2)解:∵∠BAD=60°且AC平分∠BAD,
∴∠BAC=∠DAC=30°.
由(1)知,BM=AC=AM=MC,
∴∠BAM=∠ABM,
∴∠BMC=∠BAM+∠ABM=2∠BAM=60°.
∵MN∥AD,∴∠NMC=∠DAC=30°,
∴∠BMN=∠BMC+∠NMC=90°,
∴BN2=BM2+MN2,而由(1)知,MN=BM=AC=×2=1,∴BN=.
23.(1)∵MN∥AD,∴∠NMC=∠DAC=30°,
∴∠BMN=∠BMC+∠NMC=90°,
∴BN2=BM2+MN2,而由(1)知,MN=BM=AC=×2=1,∴BN=.
(2)解:BC=2CD.理由如下:
因为CF平分∠BCD,所以∠DCE=45°.
因为∠CDE=90°,所以△CDE是等腰直角三角形,
所以CD=DE.
因为E是AD的中点,所以AD=2CD.
因为AD=BC,所以BC=2CD.
24.(1)解:四边形EBGD是菱形.理由:
∵EG垂直平分BD,
∴DF=BF,EB=ED,GB=GD,∴∠EBD=∠EDB.
∵BD是△ABC的角平分线,
∴∠EBD=∠DBC,∴∠EDF=∠GBF.
在△EFD和△GFB中,
∴△EFD≌△GFB,∴ED=BG,∴BE=ED=DG=GB,
∴四边形EBGD是菱形.
(2)解:如答图,连接EC交BD于点H,连接HG,此时HG+HC最小,作EM⊥BC于点M,DN⊥BC于点N.
在Rt△EBM中,∵∠EMB=90°,∠EBM=30°,EB=ED=2,
∴EM=BE=.
由(1)知四边形EBGD是菱形,∴DE∥BC,
∵EM⊥BC,DN⊥BC,
∴EM∥DN,EM=DN=,MN=DE=2.
在Rt△DNC中,∵∠DNC=90°,∠DCN=45°,
∴∠NDC=∠NCD=45°,
∴DN=NC=,∴MC=3.
在Rt△EMC中,∵∠EMC=90°,EM=,MC=3,
∴EC===10.
∵HG+HC=EH+HC=EC,∴HG+HC的最小值为10.
