2020—2021学年冀教版九年级数学上册第二十五章 图形的相似 测试卷(word版含答案)
文档属性
| 名称 | 2020—2021学年冀教版九年级数学上册第二十五章 图形的相似 测试卷(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 216.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-23 00:00:00 | ||
图片预览



文档简介
第二十五章
图形的相似
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.如果2a=5b,那么下列比例式中正确的是( )
A.=
B.=
C.=
D.=
2.在下列各组线段中,不成比例的是( )
A.a=3,b=6,c=2,d=4
B.a=1,b=2,c=2,d=4
C.a=4,b=6,c=5,d=10
D.a=1,b=,c=,d=
3.已知△ABC与△DEF相似,且相似比为1∶4,则△ABC与△DEF的面积比为( )
A.1∶2
B.1∶3
C.1∶4
D.1∶16
4.佳佳在家里写作业时,作业不小心被墨水污染了其中一部分(如图),则污染的部分是( )
(第4题)
A.DF
B.AC
C.EF
D.CF
5.如图,在△ABC中,点D,E分别在边AB,AC上,下列条件中不能判定△ABC∽△AED的是( )
A.∠AED=∠B
B.∠ADE=∠C
C.=
D.=
(第5题)
(第6题)
6.如图,在平行四边形ABCD中,
EF∥AB交AD于点E,交DB于点F,DE?EA=3?4,EF=3,则CD的长为( )
A.4
B.7
C.3
D.12
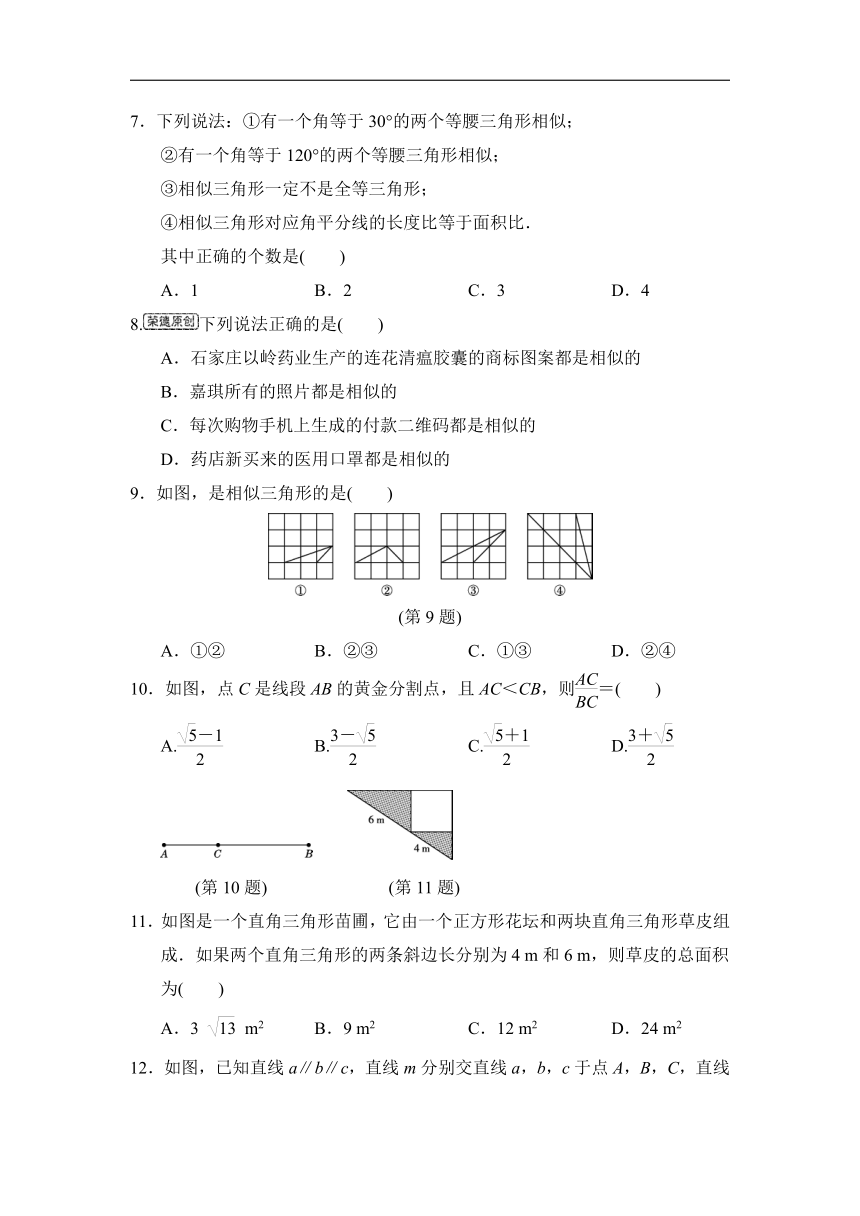
7.下列说法:①有一个角等于30°的两个等腰三角形相似;
②有一个角等于120°的两个等腰三角形相似;
③相似三角形一定不是全等三角形;
④相似三角形对应角平分线的长度比等于面积比.
其中正确的个数是( )
A.1
B.2
C.3
D.4
8.下列说法正确的是( )
A.石家庄以岭药业生产的连花清瘟胶囊的商标图案都是相似的
B.嘉琪所有的照片都是相似的
C.每次购物手机上生成的付款二维码都是相似的
D.药店新买来的医用口罩都是相似的
9.如图,是相似三角形的是( )
(第9题)
A.①②
B.②③
C.①③
D.②④
10.如图,点C是线段AB的黄金分割点,且AC<CB,则=( )
A.
B.
C.
D.
(第10题)
(第11题)
11.如图是一个直角三角形苗圃,它由一个正方形花坛和两块直角三角形草皮组成.如果两个直角三角形的两条斜边长分别为4
m和6
m,则草皮的总面积为( )
A.3
m2
B.9
m2
C.12
m2
D.24
m2
12.如图,已知直线a∥b∥c,直线m分别交直线a,b,c于点A,B,C,直线n分别交直线a,b,c于点D,E,F.若AB=3,AD=BC=5,则的值应该( )
A.等于
B.小于
C.大于
D.不能确定
(第12题)
(第13题)
13.如图,在平面直角坐标系中,点E(-4,2),点F(-1,-1),以O为位似中心,将△EFO缩小为原来的,则点E的对应点E′的坐标为( )
A.(2,-1)或(-2,1)
B.(8,-4)或(-8,4)
C.(2,-1)
D.(8,-4)
14.如图,AD为△ABC的中线,AE?EF?FD=4∶3∶1,则AG?GH?HC等于( )
A.4∶5∶3
B.3∶4∶2
C.2∶3∶1
D.1∶1∶1
(第14题)
(第15题)
15.如图,AB=4,射线BM和线段AB互相垂直,D为线段AB上一点,点E在射线BM上,且2BE=DB,作EF⊥DE,EF=DE,连接AF并延长交射线BM于点C,设BE=x,BC=y,则( )
A.y=
B.y=
C.y=
D.y=
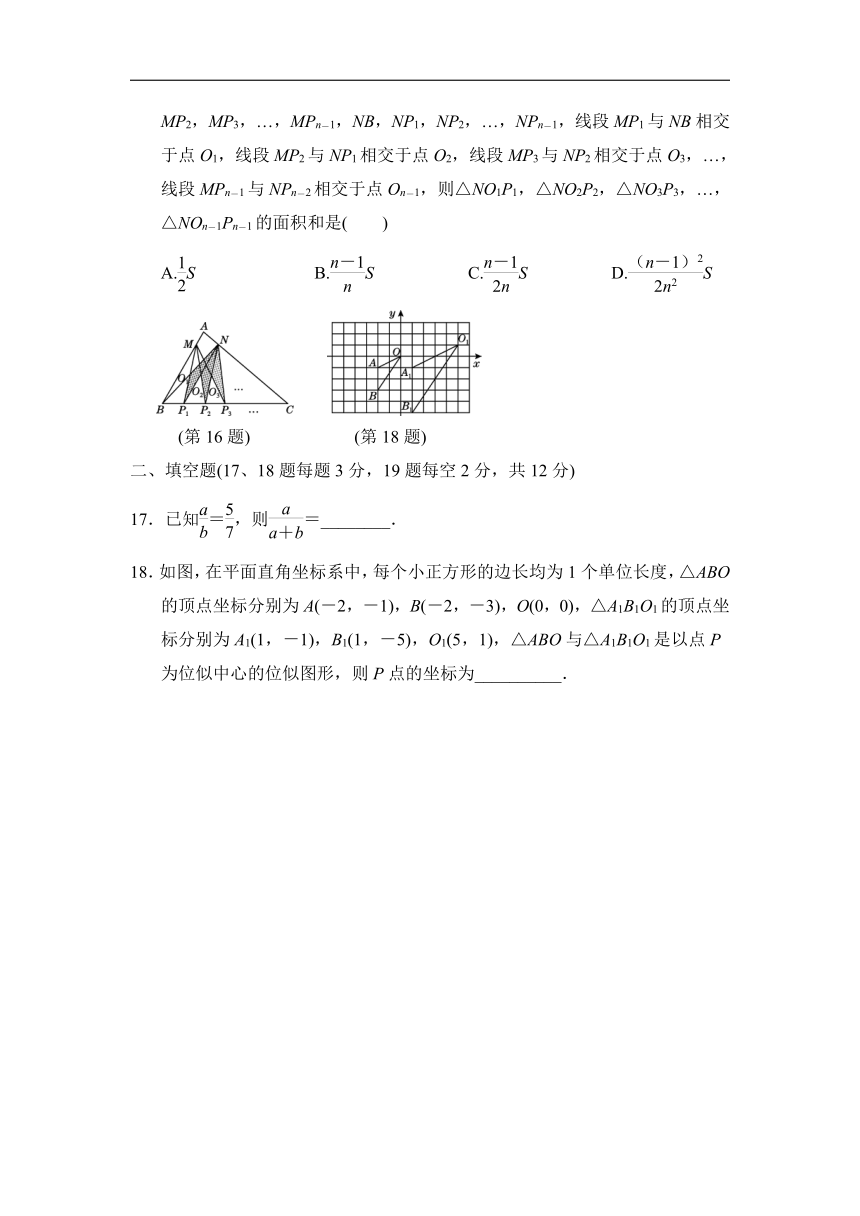
16.如图,△ABC的面积为S.点P1,P2,P3,…,Pn-1是边BC的n等分点(n≥3,且n为整数),点M,N分别在边AB,AC上,且==,连接MP1,MP2,MP3,…,MPn-1,NB,NP1,NP2,…,NPn-1,线段MP1与NB相交于点O1,线段MP2与NP1相交于点O2,线段MP3与NP2相交于点O3,…,线段MPn-1与NPn-2相交于点On-1,则△NO1P1,△NO2P2,△NO3P3,…,△NOn-1Pn-1的面积和是( )
A.S
B.S
C.S
D.S
(第16题)
(第18题)
二、填空题(17、18题每题3分,19题每空2分,共12分)
17.已知=,则=________.
18.如图,在平面直角坐标系中,每个小正方形的边长均为1个单位长度,△ABO的顶点坐标分别为A(-2,-1),B(-2,-3),O(0,0),△A1B1O1的顶点坐标分别为A1(1,-1),B1(1,-5),O1(5,1),△ABO与△A1B1O1是以点P为位似中心的位似图形,则P点的坐标为__________.
(第19题)
19.如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上.在F点观测A点后,沿FN方向走到M点,观测C点发现∠1=∠2.测得EF=15米,FM=2米,MN=8米,∠ANE=45°,则点B到河岸l的距离为________米,场地的边AB为________米,BC为________米.
三、解答题(20、21题每题8分,22、23题每题9分,24、25题每题10分,26题12分,共66分)
20.如图,△ABC在方格纸(小正方形的边长均为1)中.
(1)请在方格纸上建立平面直角坐标系,使A(3,4),C(7,3),并写出点B的坐标;
(2)以原点O为位似中心,位似比为2,在第一象限内将△ABC放大,画出放大后的位似图形△A′B′C′;
(3)计算△A′B′C′的面积S.
(第20题)
21.如图,在Rt△ABC中,∠BAC=90°,AB=AC,E,D分别是BC,AC上的点,且∠AED=45°.
(第21题)
(1)求证:△ABE∽△ECD;
(2)若AB=4,BE=,求CD的长.
22.如图,两车从路段AB两端同时出发,沿平行路线行驶(即AC∥BD),CE和DF的长分别表示两车到路段AB的距离.
(第22题)
(1)如果两车行驶速度不相同,求证:△ACE∽△BDF;
(2)添加一个条件,使△ACE≌△BDF,请说明理由.
23.如图,要从一块直角三角形的白铁皮余料ABC上截出一块矩形白铁皮EFGH.已知∠A=90°,AB=16
cm,AC=12
cm,要使截出的矩形的长与宽的比为2∶1,且较长边在BC上,点E,F分别在AB,AC上,则所截矩形的长和宽各是多少?
(第23题)
24.如图,在△ABC中,AB=10
cm,BC=20
cm,点P从点A开始沿AB边以2
cm/s的速度向点B移动,点Q从点B开始沿BC边以4
cm/s的速度向点C移动.如果点P,Q分别从A,B同时出发,问经过多久,△PBQ与△ABC相似?
(第24题)
25.如图,在△ABC中,∠C=90°,∠A=30°,BC=1,将另外一个含30°角的△EDF的30°角的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直.
(1)设AD=x,CF=y,求y与x之间的函数表达式,并直接写出函数自变量的取值范围;
(2)如果△CEF与△DEF相似,求AD的长.
(第25题)
26.如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在其右侧作正方形CDEF,连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.
(1)求的值.
(2)用含t的代数式表示△OAB的面积.
(3)是否存在点B,使以B,E,F为顶点的三角形与△OEF相似?若存在,请求出所有满足要求的B点的坐标;若不存在,请说明理由.
(第26题)
答案
一、1.C 2.C 3.D 4.C 5.D 6.B
7.A 8.A 9.C 10.A 11.C 12.C
13.A
14.B 【点拨】如图,过点D作DN∥AC,分别交BG,BH于点N,M,
∴易得=,=.
∵AE∶EF∶FD=4∶3∶1,
∴===1,===,∴DN=AG,DM=AH.
∵AD是△ABC的中线,
∴点D是BC的中点,
又∵DN∥AC,
∴点N是BG的中点,点M是BH的中点,
∴DN=CG,DM=CH,
∴AG=CG,CH=AH.
∵AG+CG=AC,CH+AH=AC,
∴AG=AC,CH=AC,
∴GH=AC-AG-CH=AC-AC-AC=AC,∴AG∶GH∶HC=AC∶AC∶AC=3∶4∶2.
(第14题)
15.A 【点拨】过点F作FG⊥BC于G,
∵∠DBE=∠DEF=90°,
∴∠BDE+∠BED=∠BED+∠FEG=90°,∴∠BDE=∠FEG.
又∵∠DBE=∠EGF=90°,
∴△DBE∽△EGF.∴==.
∵EF=DE,2BE=DB,BE=x,
∴FG=BE=x,EG=DB=x.
∵AB⊥BM,FG⊥BM,
∴FG∥AB,∴△CFG∽△CAB.
∴=.
∴=,整理得y=.
16.D 【点拨】连接MN,
∵==,∠A=∠A,
∴△AMN∽△ABC.
∴==,∠AMN=∠ABC.
∴MN∥BC.
∵点P1,P2,P3,…,Pn-1是边BC的n等分点,∴MN=BP1=P1P2=P2P3=…=Pn-1C.
∴四边形MNP1B,四边形MNP2P1,四边形MNP3P2,…,四边形MNPn-1Pn-2都是平行四边形.
易知S△BCN=S,S△MNB=S,
∴S△BP1O1=S△P1P2O2=S△P3P2O3=…=S△Pn-2Pn-1On-1=S.
∴S阴=S△NBC-(n-1)·S△BP1O1-S△NPn-1C=S-(n-1)·S-S=S.
二、17. 18.(-5,-1)
19.10;15
;20
【点拨】∵AE⊥l,BF⊥l,∠ANE=45°,
∴△ANE和△BNF都是等腰直角三角形,∴AE=EN,BF=FN.
∵EF=15米,FM=2米,MN=8米,
∴AE=EN=15+2+8=25(米),
BF=FN=2+8=10(米).
∴AN=25
米,BN=10
米,
∴AB=AN-BN=15
米.
如图,过C作CH⊥l于H,过B作PQ∥l交AE于点P,交CH于点Q,
∴AE∥CH∥BF,
∴易得四边形PEHQ和四边形PEFB是矩形,
∴PE=BF=QH=10米,PB=EF=15米,BQ=FH,
∵∠1=∠2,∠AEF=∠CHM=90°,
∴△AEF∽△CHM,
∴===,
∴设MH=3x米,CH=5x米,∴CQ=(5x-10)米,BQ=FH=(3x+2)米,
∵∠APB=∠ABC=∠CQB=90°,
∴∠ABP+∠PAB=∠ABP+∠CBQ=90°,∴∠PAB=∠CBQ,
∴△APB∽△BQC,∴=,
∴=,∴x=6,
∴BQ=CQ=20米,∴BC=20
米.
(第19题)
三、20.解:(1)建立平面直角坐标系如图所示.点B的坐标为(3,2).
(第20题)
(2)如图所示.
(3)△A′B′C′的面积S=×4×8=16.
21.(1)证明:在Rt△ABC中,∠BAC=90°,AB=AC,∴∠B=∠C=45°.
∵∠AEC=∠B+∠BAE=∠AED+∠CED,∠AED=45°,∴∠BAE=∠CED.∴△ABE∽△ECD.
(2)解:在Rt△ABC中,∠BAC=90°,AB=AC=4,∴BC=4
.
∵BE=,∴EC=3
.
∵△ABE∽△ECD,
∴=,即=,
解得CD=.
22.(1)证明:∵AC∥BD,∴∠A=∠B,
∵CE⊥AB,DF⊥AB,
∴∠CEA=∠DFB=90°,
∴△ACE∽△BDF.
(2)解:添加的条件为两车等速行驶.
理由:∵AC∥BD,∴∠A=∠B.
∵CE⊥AB,DF⊥AB,
∴∠CEA=∠DFB=90°.
∵两车等速同时行驶,∴AC=BD.
在△ACE和△BDF中,
∴△ACE≌△BDF.
23.解:过点A作AN⊥BC交EF于点M,交BC于点N.
∵∠BAC=90°,
∴∠BNA=∠BAC,BC==20
cm.
又∵∠B=∠B,
∴△ABN∽△CBA.∴=.
∴AN==
cm.
∵四边形EFGH是矩形,
∴EF∥HG.
∴∠AEF=∠B,∠AFE=∠C.
∴△AEF∽△ABC.∴=.
设FG=x
cm,则MN=x
cm,EF=2x
cm.∴=,
解得x=.∴2x=.
答:所截矩形的长是cm,宽是
cm.
24.解:设经过t
s,△PBQ与△ABC相似.
由题意得AP=2t
cm,BQ=4t
cm,BP=(10-2t)cm.
当△PBQ∽△ABC时,有=,
即=,解得t=2.5;
当△QBP∽△ABC时,有=,
即=,解得t=1.
综上所述,经过2.5
s或1
s,△PBQ与△ABC相似.
25.解:(1)∵∠EDF=30°,ED⊥AB于点D,∴∠FDB=60°.
∵∠C=90°,∠A=30°,∴∠B=60°.
∴△BDF是等边三角形.∴BD=BF.∵BC=1,∠A=30°,∴AB=2,
∴2-x=1-y,∴y=x-1.
自变量的取值范围是1≤x≤.
(2)①如图①,当△CEF∽△EDF时,
=,∠CEF=∠EDF=30°.
∵CF=y,∴EF=2y.
∵△BDF是等边三角形,
∴DF=BF=1-y.
∴=.解得y=.
∵AD=x,y=x-1,
∴AD=1+=;
(第25题)
②如图②,当△CEF∽△FED时,
=,∠CFE=∠FDE=30°.
∴CE=EF.∴=,
解得y=,∴AD=1+=.
∴AD的长为或.
26.解:(1)∵A(2,2),∴∠AOD=45°.
∴△OCD是等腰直角三角形.
∵OD=t,∴正方形CDEF的边长为t.
∴OE=OD+DE=t+t=2t.
∴==.
(2)∵A(2,2),∴OA=2
.
∵OD=t,∴OC=t.
∴AC=OA-OC=2
-t.
∵四边形CDEF是正方形,
∴CF∥OB.∴△ACF∽△AOB.
∴=,即=.
解得OB=.
∴易得S△OAB=(0<t<2).
(3)存在.
要使△BEF与△OEF相似,
∵∠FEO=∠FEB=90°,
∴只要=或=即可,
即=或=.
解得BE=2t或BE=t.
①当BE=2t时,BO=4t,
∴=4t.解得t=0(舍去)或t=.∴B(6,0).
②当BE=t时,若B在E的左侧,
则OB=OE-EB=2t-t=t,
∴=t.解得t=0(舍去)或t=.∴B(1,0);
若B在E的右侧,则OB=OE+EB=2t+t=t,∴=t.
解得t=0(舍去)或t=.∴B(3,0).
综上所述,B点的坐标为(6,0)或(1,0)或(3,0).
图形的相似
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.如果2a=5b,那么下列比例式中正确的是( )
A.=
B.=
C.=
D.=
2.在下列各组线段中,不成比例的是( )
A.a=3,b=6,c=2,d=4
B.a=1,b=2,c=2,d=4
C.a=4,b=6,c=5,d=10
D.a=1,b=,c=,d=
3.已知△ABC与△DEF相似,且相似比为1∶4,则△ABC与△DEF的面积比为( )
A.1∶2
B.1∶3
C.1∶4
D.1∶16
4.佳佳在家里写作业时,作业不小心被墨水污染了其中一部分(如图),则污染的部分是( )
(第4题)
A.DF
B.AC
C.EF
D.CF
5.如图,在△ABC中,点D,E分别在边AB,AC上,下列条件中不能判定△ABC∽△AED的是( )
A.∠AED=∠B
B.∠ADE=∠C
C.=
D.=
(第5题)
(第6题)
6.如图,在平行四边形ABCD中,
EF∥AB交AD于点E,交DB于点F,DE?EA=3?4,EF=3,则CD的长为( )
A.4
B.7
C.3
D.12
7.下列说法:①有一个角等于30°的两个等腰三角形相似;
②有一个角等于120°的两个等腰三角形相似;
③相似三角形一定不是全等三角形;
④相似三角形对应角平分线的长度比等于面积比.
其中正确的个数是( )
A.1
B.2
C.3
D.4
8.下列说法正确的是( )
A.石家庄以岭药业生产的连花清瘟胶囊的商标图案都是相似的
B.嘉琪所有的照片都是相似的
C.每次购物手机上生成的付款二维码都是相似的
D.药店新买来的医用口罩都是相似的
9.如图,是相似三角形的是( )
(第9题)
A.①②
B.②③
C.①③
D.②④
10.如图,点C是线段AB的黄金分割点,且AC<CB,则=( )
A.
B.
C.
D.
(第10题)
(第11题)
11.如图是一个直角三角形苗圃,它由一个正方形花坛和两块直角三角形草皮组成.如果两个直角三角形的两条斜边长分别为4
m和6
m,则草皮的总面积为( )
A.3
m2
B.9
m2
C.12
m2
D.24
m2
12.如图,已知直线a∥b∥c,直线m分别交直线a,b,c于点A,B,C,直线n分别交直线a,b,c于点D,E,F.若AB=3,AD=BC=5,则的值应该( )
A.等于
B.小于
C.大于
D.不能确定
(第12题)
(第13题)
13.如图,在平面直角坐标系中,点E(-4,2),点F(-1,-1),以O为位似中心,将△EFO缩小为原来的,则点E的对应点E′的坐标为( )
A.(2,-1)或(-2,1)
B.(8,-4)或(-8,4)
C.(2,-1)
D.(8,-4)
14.如图,AD为△ABC的中线,AE?EF?FD=4∶3∶1,则AG?GH?HC等于( )
A.4∶5∶3
B.3∶4∶2
C.2∶3∶1
D.1∶1∶1
(第14题)
(第15题)
15.如图,AB=4,射线BM和线段AB互相垂直,D为线段AB上一点,点E在射线BM上,且2BE=DB,作EF⊥DE,EF=DE,连接AF并延长交射线BM于点C,设BE=x,BC=y,则( )
A.y=
B.y=
C.y=
D.y=
16.如图,△ABC的面积为S.点P1,P2,P3,…,Pn-1是边BC的n等分点(n≥3,且n为整数),点M,N分别在边AB,AC上,且==,连接MP1,MP2,MP3,…,MPn-1,NB,NP1,NP2,…,NPn-1,线段MP1与NB相交于点O1,线段MP2与NP1相交于点O2,线段MP3与NP2相交于点O3,…,线段MPn-1与NPn-2相交于点On-1,则△NO1P1,△NO2P2,△NO3P3,…,△NOn-1Pn-1的面积和是( )
A.S
B.S
C.S
D.S
(第16题)
(第18题)
二、填空题(17、18题每题3分,19题每空2分,共12分)
17.已知=,则=________.
18.如图,在平面直角坐标系中,每个小正方形的边长均为1个单位长度,△ABO的顶点坐标分别为A(-2,-1),B(-2,-3),O(0,0),△A1B1O1的顶点坐标分别为A1(1,-1),B1(1,-5),O1(5,1),△ABO与△A1B1O1是以点P为位似中心的位似图形,则P点的坐标为__________.
(第19题)
19.如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上.在F点观测A点后,沿FN方向走到M点,观测C点发现∠1=∠2.测得EF=15米,FM=2米,MN=8米,∠ANE=45°,则点B到河岸l的距离为________米,场地的边AB为________米,BC为________米.
三、解答题(20、21题每题8分,22、23题每题9分,24、25题每题10分,26题12分,共66分)
20.如图,△ABC在方格纸(小正方形的边长均为1)中.
(1)请在方格纸上建立平面直角坐标系,使A(3,4),C(7,3),并写出点B的坐标;
(2)以原点O为位似中心,位似比为2,在第一象限内将△ABC放大,画出放大后的位似图形△A′B′C′;
(3)计算△A′B′C′的面积S.
(第20题)
21.如图,在Rt△ABC中,∠BAC=90°,AB=AC,E,D分别是BC,AC上的点,且∠AED=45°.
(第21题)
(1)求证:△ABE∽△ECD;
(2)若AB=4,BE=,求CD的长.
22.如图,两车从路段AB两端同时出发,沿平行路线行驶(即AC∥BD),CE和DF的长分别表示两车到路段AB的距离.
(第22题)
(1)如果两车行驶速度不相同,求证:△ACE∽△BDF;
(2)添加一个条件,使△ACE≌△BDF,请说明理由.
23.如图,要从一块直角三角形的白铁皮余料ABC上截出一块矩形白铁皮EFGH.已知∠A=90°,AB=16
cm,AC=12
cm,要使截出的矩形的长与宽的比为2∶1,且较长边在BC上,点E,F分别在AB,AC上,则所截矩形的长和宽各是多少?
(第23题)
24.如图,在△ABC中,AB=10
cm,BC=20
cm,点P从点A开始沿AB边以2
cm/s的速度向点B移动,点Q从点B开始沿BC边以4
cm/s的速度向点C移动.如果点P,Q分别从A,B同时出发,问经过多久,△PBQ与△ABC相似?
(第24题)
25.如图,在△ABC中,∠C=90°,∠A=30°,BC=1,将另外一个含30°角的△EDF的30°角的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直.
(1)设AD=x,CF=y,求y与x之间的函数表达式,并直接写出函数自变量的取值范围;
(2)如果△CEF与△DEF相似,求AD的长.
(第25题)
26.如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在其右侧作正方形CDEF,连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.
(1)求的值.
(2)用含t的代数式表示△OAB的面积.
(3)是否存在点B,使以B,E,F为顶点的三角形与△OEF相似?若存在,请求出所有满足要求的B点的坐标;若不存在,请说明理由.
(第26题)
答案
一、1.C 2.C 3.D 4.C 5.D 6.B
7.A 8.A 9.C 10.A 11.C 12.C
13.A
14.B 【点拨】如图,过点D作DN∥AC,分别交BG,BH于点N,M,
∴易得=,=.
∵AE∶EF∶FD=4∶3∶1,
∴===1,===,∴DN=AG,DM=AH.
∵AD是△ABC的中线,
∴点D是BC的中点,
又∵DN∥AC,
∴点N是BG的中点,点M是BH的中点,
∴DN=CG,DM=CH,
∴AG=CG,CH=AH.
∵AG+CG=AC,CH+AH=AC,
∴AG=AC,CH=AC,
∴GH=AC-AG-CH=AC-AC-AC=AC,∴AG∶GH∶HC=AC∶AC∶AC=3∶4∶2.
(第14题)
15.A 【点拨】过点F作FG⊥BC于G,
∵∠DBE=∠DEF=90°,
∴∠BDE+∠BED=∠BED+∠FEG=90°,∴∠BDE=∠FEG.
又∵∠DBE=∠EGF=90°,
∴△DBE∽△EGF.∴==.
∵EF=DE,2BE=DB,BE=x,
∴FG=BE=x,EG=DB=x.
∵AB⊥BM,FG⊥BM,
∴FG∥AB,∴△CFG∽△CAB.
∴=.
∴=,整理得y=.
16.D 【点拨】连接MN,
∵==,∠A=∠A,
∴△AMN∽△ABC.
∴==,∠AMN=∠ABC.
∴MN∥BC.
∵点P1,P2,P3,…,Pn-1是边BC的n等分点,∴MN=BP1=P1P2=P2P3=…=Pn-1C.
∴四边形MNP1B,四边形MNP2P1,四边形MNP3P2,…,四边形MNPn-1Pn-2都是平行四边形.
易知S△BCN=S,S△MNB=S,
∴S△BP1O1=S△P1P2O2=S△P3P2O3=…=S△Pn-2Pn-1On-1=S.
∴S阴=S△NBC-(n-1)·S△BP1O1-S△NPn-1C=S-(n-1)·S-S=S.
二、17. 18.(-5,-1)
19.10;15
;20
【点拨】∵AE⊥l,BF⊥l,∠ANE=45°,
∴△ANE和△BNF都是等腰直角三角形,∴AE=EN,BF=FN.
∵EF=15米,FM=2米,MN=8米,
∴AE=EN=15+2+8=25(米),
BF=FN=2+8=10(米).
∴AN=25
米,BN=10
米,
∴AB=AN-BN=15
米.
如图,过C作CH⊥l于H,过B作PQ∥l交AE于点P,交CH于点Q,
∴AE∥CH∥BF,
∴易得四边形PEHQ和四边形PEFB是矩形,
∴PE=BF=QH=10米,PB=EF=15米,BQ=FH,
∵∠1=∠2,∠AEF=∠CHM=90°,
∴△AEF∽△CHM,
∴===,
∴设MH=3x米,CH=5x米,∴CQ=(5x-10)米,BQ=FH=(3x+2)米,
∵∠APB=∠ABC=∠CQB=90°,
∴∠ABP+∠PAB=∠ABP+∠CBQ=90°,∴∠PAB=∠CBQ,
∴△APB∽△BQC,∴=,
∴=,∴x=6,
∴BQ=CQ=20米,∴BC=20
米.
(第19题)
三、20.解:(1)建立平面直角坐标系如图所示.点B的坐标为(3,2).
(第20题)
(2)如图所示.
(3)△A′B′C′的面积S=×4×8=16.
21.(1)证明:在Rt△ABC中,∠BAC=90°,AB=AC,∴∠B=∠C=45°.
∵∠AEC=∠B+∠BAE=∠AED+∠CED,∠AED=45°,∴∠BAE=∠CED.∴△ABE∽△ECD.
(2)解:在Rt△ABC中,∠BAC=90°,AB=AC=4,∴BC=4
.
∵BE=,∴EC=3
.
∵△ABE∽△ECD,
∴=,即=,
解得CD=.
22.(1)证明:∵AC∥BD,∴∠A=∠B,
∵CE⊥AB,DF⊥AB,
∴∠CEA=∠DFB=90°,
∴△ACE∽△BDF.
(2)解:添加的条件为两车等速行驶.
理由:∵AC∥BD,∴∠A=∠B.
∵CE⊥AB,DF⊥AB,
∴∠CEA=∠DFB=90°.
∵两车等速同时行驶,∴AC=BD.
在△ACE和△BDF中,
∴△ACE≌△BDF.
23.解:过点A作AN⊥BC交EF于点M,交BC于点N.
∵∠BAC=90°,
∴∠BNA=∠BAC,BC==20
cm.
又∵∠B=∠B,
∴△ABN∽△CBA.∴=.
∴AN==
cm.
∵四边形EFGH是矩形,
∴EF∥HG.
∴∠AEF=∠B,∠AFE=∠C.
∴△AEF∽△ABC.∴=.
设FG=x
cm,则MN=x
cm,EF=2x
cm.∴=,
解得x=.∴2x=.
答:所截矩形的长是cm,宽是
cm.
24.解:设经过t
s,△PBQ与△ABC相似.
由题意得AP=2t
cm,BQ=4t
cm,BP=(10-2t)cm.
当△PBQ∽△ABC时,有=,
即=,解得t=2.5;
当△QBP∽△ABC时,有=,
即=,解得t=1.
综上所述,经过2.5
s或1
s,△PBQ与△ABC相似.
25.解:(1)∵∠EDF=30°,ED⊥AB于点D,∴∠FDB=60°.
∵∠C=90°,∠A=30°,∴∠B=60°.
∴△BDF是等边三角形.∴BD=BF.∵BC=1,∠A=30°,∴AB=2,
∴2-x=1-y,∴y=x-1.
自变量的取值范围是1≤x≤.
(2)①如图①,当△CEF∽△EDF时,
=,∠CEF=∠EDF=30°.
∵CF=y,∴EF=2y.
∵△BDF是等边三角形,
∴DF=BF=1-y.
∴=.解得y=.
∵AD=x,y=x-1,
∴AD=1+=;
(第25题)
②如图②,当△CEF∽△FED时,
=,∠CFE=∠FDE=30°.
∴CE=EF.∴=,
解得y=,∴AD=1+=.
∴AD的长为或.
26.解:(1)∵A(2,2),∴∠AOD=45°.
∴△OCD是等腰直角三角形.
∵OD=t,∴正方形CDEF的边长为t.
∴OE=OD+DE=t+t=2t.
∴==.
(2)∵A(2,2),∴OA=2
.
∵OD=t,∴OC=t.
∴AC=OA-OC=2
-t.
∵四边形CDEF是正方形,
∴CF∥OB.∴△ACF∽△AOB.
∴=,即=.
解得OB=.
∴易得S△OAB=(0<t<2).
(3)存在.
要使△BEF与△OEF相似,
∵∠FEO=∠FEB=90°,
∴只要=或=即可,
即=或=.
解得BE=2t或BE=t.
①当BE=2t时,BO=4t,
∴=4t.解得t=0(舍去)或t=.∴B(6,0).
②当BE=t时,若B在E的左侧,
则OB=OE-EB=2t-t=t,
∴=t.解得t=0(舍去)或t=.∴B(1,0);
若B在E的右侧,则OB=OE+EB=2t+t=t,∴=t.
解得t=0(舍去)或t=.∴B(3,0).
综上所述,B点的坐标为(6,0)或(1,0)或(3,0).
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
