2020-2021学年苏科版七年级数学下册11.4解一元一次不等式(1)培优训练(机构)(word解析版)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册11.4解一元一次不等式(1)培优训练(机构)(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 609.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 10:15:50 | ||
图片预览




文档简介
11.4解一元一次不等式(1)-苏科版七年级数学下册
培优训练
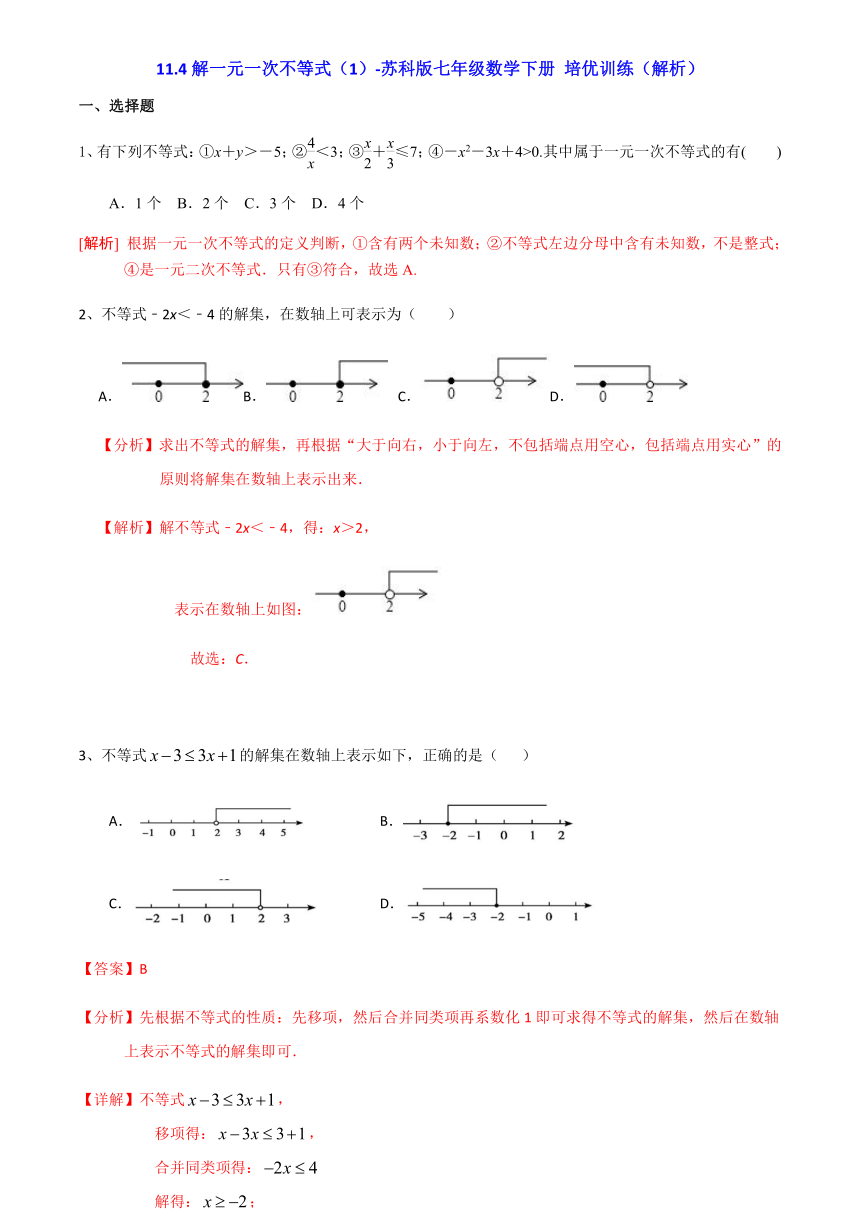
一、选择题
1、有下列不等式:①x+y>-5;②<3;③+≤7;④-x2-3x+4>0.其中属于一元一次不等式的有( )
A.1个
B.2个
C.3个
D.4个
2、不等式﹣2x<﹣4的解集,在数轴上可表示为( )
A.B.
C.D.
3、不等式的解集在数轴上表示如下,正确的是(
)
A.
B.
C.
D.
4、不等式x+1≥2x-1的解集在数轴上的表示为( )
A.
B.
C,
D.
5、如果不等式ax>1的解集是x<,那么( )
A.a≥0
B.a≤0
C.a>0
D.a<0
6、一元一次不等式的解集在数轴上表示为(
)
A.B.C.
D.
7、若2x+1为非负数,则x的取值范围是( )
A.x≥1
B.x≥-
C.x>1
D.x>-
8、已知(k+3)x|k|﹣2+5<k﹣4是关于x的一元一次不等式,则不等式的解集是( )
A.x<1
B.x<﹣1
C.x<2
D.x>﹣1
9、阅读理解:我们把称作二阶行列式,规定它的运算法则为=ad-bc,
例如=1×4-3×2=-2.如果>3,那么x的取值范围是( )
A.x>2
B.x<-2
C.x>6
D.x<-6
10、若方程组
的解满足3x-4y>0,则k的取值范围是( )
A.k>1
B.k<1
C.k>-1
D.k<-1
二、填空题
11、若3xm-1-2>1是关于x的一元一次不等式,则m=________.
12、已知(k-3)x|k|-2+5<k-4是关于x的一元一次不等式,求k的值=__________.
13、不等式2ax>3a的两边都除以2a,写出不等式的解集:
(1)当a>0时,得____________;
(2)当a<0时,得____________.
14、已知代数式-4x+5,当x________时,它的值是正数;当x________时,它的值是负数;
当x________时,它的值不小于2;
当x________时,它的值不大于1.
15、已知关于x的不等式x-a<1的解集如图所示,则a的值为________.
16、已知关于x的不等式2x﹣a>﹣3的解集是x>1,则a的值为
.
17、关于x的不等式2x-a≤-3的解集如图所示,则a的值是______
.
18、若方程2x=4的解使关于x的一元一次不等式xA.a>3
B.a>-3
C.a<3
D.a<-3
19、定义一种新运算“?”,其运算规则为:a?b=-2a+3b.如:1?5=-2×1+3×5=13.
则不等式x?4<0的解集为________.
20、不等式10﹣5x≥0的所有非负整数解的积为 .
三、解答题
21、解下列不等式,并把解集表示在数轴上.
(1)x+2<1;
(2)2x-3≥0;
(3)4x-622、解下列不等式,并把它们的解集在数轴上表示出来.
(1)6a+8<7a-6;
(2)8-2x≥5x-6.
23、已知关于x的方程5x-10k=20的解是非负数,求k的取值范围.
24、定义新运算:对于任意有理数a,b,都有a?b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算.例如:2?5=2×(2-5)+1=2×(-3)+1=-6+1=-5.
(1)求(-2)?3的值;
(2)若3?x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.
25、(1)已知关于x,y的方程组的解满足不等式x+y>3,求a的取值范围.
(2)已知关于x,y的方程组的解满足不等式x+y<3,求a的取值范围.
26、已知关于x的方程3(x-2a)+2=2x-a+1的解不适合不等式2x-10>8a,求a的取值范围.
11.4解一元一次不等式(1)-苏科版七年级数学下册
培优训练(解析)
一、选择题
1、有下列不等式:①x+y>-5;②<3;③+≤7;④-x2-3x+4>0.其中属于一元一次不等式的有( )
A.1个
B.2个
C.3个
D.4个
[解析]
根据一元一次不等式的定义判断,①含有两个未知数;②不等式左边分母中含有未知数,不是整式;④是一元二次不等式.只有③符合,故选A.
2、不等式﹣2x<﹣4的解集,在数轴上可表示为( )
A.B.
C.D.
【分析】求出不等式的解集,再根据“大于向右,小于向左,不包括端点用空心,包括端点用实心”的原则将解集在数轴上表示出来.
【解析】解不等式﹣2x<﹣4,得:x>2,
表示在数轴上如图:
故选:C.
3、不等式的解集在数轴上表示如下,正确的是(
)
A.
B.
C.
D.
【答案】B
【分析】先根据不等式的性质:先移项,然后合并同类项再系数化1即可求得不等式的解集,然后在数轴上表示不等式的解集即可.
【详解】不等式,
移项得:,
合并同类项得:
解得:;
在数轴上表示为:
故选:B.
4、不等式x+1≥2x-1的解集在数轴上的表示为( )
A.
B.
C,
D.
[解析]
由x+1≥2x-1得x-2x≥-1-1,则
-x≥-2,从而x≤2.故选B.
5、如果不等式ax>1的解集是x<,那么( )
A.a≥0
B.a≤0
C.a>0
D.a<0
[解析]
根据不等式的基本性质解答,由于不等号的方向发生了改变,所以可判定a为负数.
故选D.
6、一元一次不等式的解集在数轴上表示为(
)
A.B.C.
D.
【答案】B
【分析】先求出不等式的解集,再在数轴上表示出不等式的解集即可.
【详解】-3x-1>2,
-3x>2+1,
-3x>3,
x<-1,
在数轴上表示为:,
故选B.
7、若2x+1为非负数,则x的取值范围是( )
A.x≥1
B.x≥-
C.x>1
D.x>-
[解析]
由题意得2x+1≥0,解得x≥-,故选B.
8、已知(k+3)x|k|﹣2+5<k﹣4是关于x的一元一次不等式,则不等式的解集是( )
A.x<1
B.x<﹣1
C.x<2
D.x>﹣1
【分析】先根据一元一次不等式的概念得出k的值,代入不等式,解之可得.
【解析】∵(k+3)x|k|﹣2+5<k﹣4是关于x的一元一次不等式,
∴k+3≠0且|k|﹣2=1,
解得k=3,
则不等式为6x+5<3﹣4,
解得x<﹣1,
故选:B.
9、阅读理解:我们把称作二阶行列式,规定它的运算法则为=ad-bc,
例如=1×4-3×2=-2.如果>3,那么x的取值范围是( )
A.x>2
B.x<-2
C.x>6
D.x<-6
[解析]
由题意可得2x-(3-x)>3,解得x>2.故选A.
10、若方程组
的解满足3x-4y>0,则k的取值范围是( )
A.k>1
B.k<1
C.k>-1
D.k<-1
[解析]
①-②,得3x-4y=1-k,
由3x-4y>0,得1-k>0,解得k<1.
故选B.
二、填空题
11、若3xm-1-2>1是关于x的一元一次不等式,则m=________.
[答案]
2
[解析]
根据一元一次不等式的概念,知m-1=1,解得m=2.
12、已知(k-3)x|k|-2+5<k-4是关于x的一元一次不等式,求k的值=__________.
解:根据一元一次不等式的定义,有|k|-2=1,且k-3≠0,因此k=-3.
13、不等式2ax>3a的两边都除以2a,写出不等式的解集:
(1)当a>0时,得____________;
(2)当a<0时,得____________.
答案:(1)x> (2)x< [解析]
依据不等式的基本性质2,要注意a的正负.
14、已知代数式-4x+5,当x________时,它的值是正数;当x________时,它的值是负数;
当x________时,它的值不小于2;
当x________时,它的值不大于1.
答案:< > ≤ ≥1
[解析]
根据题意列出不等式,再解不等式.
-4x+5>0,x<;
-4x+5<0,x>;
-4x+52,x≤;
-4x+51,x≥1
15、已知关于x的不等式x-a<1的解集如图所示,则a的值为________.
[答案]
1
[解析]
由图可知x<2.因为解不等式x-a<1得x<1+a,所以1+a=2,解得a=1.
16、已知关于x的不等式2x﹣a>﹣3的解集是x>1,则a的值为
.
【分析】根据解一元一次不等式的方法和题意,可以求得a的值,本题得以解决.
【解析】由2x﹣a>﹣3,得x,
∵不等式2x﹣a>﹣3的解集是x>1,
∴=1,
解得,a=5,
故答案为:5.
17、关于x的不等式2x-a≤-3的解集如图所示,则a的值是______
.
【答案】1
【分析】首先用a表示出不等式的解集,然后解出a.
【详解】∵2x-a≤-3,
∴x≤,
∵x≤-1,
∴a=1.
故答案为1.
18、若方程2x=4的解使关于x的一元一次不等式xA.a>3
B.a>-3
C.a<3
D.a<-3
[解析]
由2x=4,得x=2,将x=2代入x-3.
故选B.
19、定义一种新运算“?”,其运算规则为:a?b=-2a+3b.如:1?5=-2×1+3×5=13.
则不等式x?4<0的解集为________.
[答案]
x>6
[解析]
根据题意,得x?4=-2x+3×4=-2x+12.因为x?4<0,所以-2x+12<0,解得x>6.
20、不等式10﹣5x≥0的所有非负整数解的积为 .
【分析】先求出不等式的解集,再求出不等式的非负整数解,即可得出答案.
【解析】10﹣5x≥0,
﹣5x≥﹣10,
x≤2,
所以不等式的非负整数解为0,1,2,
0×1×2=0,
故答案为:0.
三、解答题
21、解下列不等式,并把解集表示在数轴上.
(1)x+2<1;
(2)2x-3≥0;
(3)4x-6[解析]
(1)不等式两边都减去2;(2)不等式两边都加上3,然后两边都除以2,不等号的方向不变;
(3)不等式两边都减去(x-6),然后两边都除以3,不等号的方向不变.
解:(1)根据不等式的基本性质1,在不等式的两边都减去2,不等号的方向不变,得
x+2-2<1-2,即x<-1,
这个不等式的解集在数轴上的表示如图所示:
(2)根据不等式的基本性质1,在不等式的两边都加上3,得2x-3+3≥0+3,即2x≥3,
根据不等式的基本性质2,不等式的两边同时除以2,不等号的方向不变,得x≥,
这个不等式的解集在数轴上的表示如图所示:
(3)根据不等式的基本性质1,在不等式的两边都减去(x-6),得
4x-6-(x-6)根据不等式的基本性质2,不等式的两边同时除以3,不等号的方向不变,得x<2,
这个不等式的解集在数轴上的表示如图所示:
22、解下列不等式,并把它们的解集在数轴上表示出来.
(1)6a+8<7a-6;
(2)8-2x≥5x-6.
解:(1)移项,得6a-7a<-6-8,
合并同类项,得-a<-14,
系数化为1,得a>14.
在数轴上表示解集如下:
(2)移项,得-2x-5x≥-6-8,
合并同类项,得-7x≥-14,
系数化为1,得x≤2.
在数轴上表示解集如下:
23、已知关于x的方程5x-10k=20的解是非负数,求k的取值范围.
[解析]
先解关于x的方程,用含k的代数式表示方程的解,再由x是非负数这一条件列出不等式,从而确定k的取值范围.
解:解方程5x-10k=20,得x=2k+4.
因为x是非负数,所以2k+4≥0.
不等式两边都减去4,得2k≥-4,
不等式两边都除以2,得k≥-2.
所以k的取值范围是k≥-2.
24、定义新运算:对于任意有理数a,b,都有a?b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算.例如:2?5=2×(2-5)+1=2×(-3)+1=-6+1=-5.
(1)求(-2)?3的值;
(2)若3?x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.
解:(1)(-2)?3=-2×(-2-3)+1=-2×(-5)+1=10+1=11.
(2)∵3?x<13,∴3(3-x)+1<13,
∴9-3x+1<13,即-3x<3,∴x>-1.
在数轴上表示如图所示:
25、(1)已知关于x,y的方程组的解满足不等式x+y>3,求a的取值范围.
(2)已知关于x,y的方程组的解满足不等式x+y<3,求a的取值范围.
解:(1)
①+②,得3x=6a+3,即x=2a+1.
将x=2a+1代入①,得2a+1-y=3a+3,解得y=-a-2.
所以方程组的解为
因为方程组的解满足不等式x+y>3,
所以2a+1+(-a-2)>3,
解得a>4.
(2)
①+②,得3x=6a+3,解得x=2a+1.
将x=2a+1代入①,得y=2a-2.
因为x+y<3,所以2a+1+2a-2<3,
即4a<4,
所以a<1.
26、已知关于x的方程3(x-2a)+2=2x-a+1的解不适合不等式2x-10>8a,求a的取值范围.
解:方程3(x-2a)+2=2x-a+1的解为x=5a-1,
不等式2x-10>8a的解集是x>4a+5.
根据题意,得5a-1≤4a+5,
∴
培优训练
一、选择题
1、有下列不等式:①x+y>-5;②<3;③+≤7;④-x2-3x+4>0.其中属于一元一次不等式的有( )
A.1个
B.2个
C.3个
D.4个
2、不等式﹣2x<﹣4的解集,在数轴上可表示为( )
A.B.
C.D.
3、不等式的解集在数轴上表示如下,正确的是(
)
A.
B.
C.
D.
4、不等式x+1≥2x-1的解集在数轴上的表示为( )
A.
B.
C,
D.
5、如果不等式ax>1的解集是x<,那么( )
A.a≥0
B.a≤0
C.a>0
D.a<0
6、一元一次不等式的解集在数轴上表示为(
)
A.B.C.
D.
7、若2x+1为非负数,则x的取值范围是( )
A.x≥1
B.x≥-
C.x>1
D.x>-
8、已知(k+3)x|k|﹣2+5<k﹣4是关于x的一元一次不等式,则不等式的解集是( )
A.x<1
B.x<﹣1
C.x<2
D.x>﹣1
9、阅读理解:我们把称作二阶行列式,规定它的运算法则为=ad-bc,
例如=1×4-3×2=-2.如果>3,那么x的取值范围是( )
A.x>2
B.x<-2
C.x>6
D.x<-6
10、若方程组
的解满足3x-4y>0,则k的取值范围是( )
A.k>1
B.k<1
C.k>-1
D.k<-1
二、填空题
11、若3xm-1-2>1是关于x的一元一次不等式,则m=________.
12、已知(k-3)x|k|-2+5<k-4是关于x的一元一次不等式,求k的值=__________.
13、不等式2ax>3a的两边都除以2a,写出不等式的解集:
(1)当a>0时,得____________;
(2)当a<0时,得____________.
14、已知代数式-4x+5,当x________时,它的值是正数;当x________时,它的值是负数;
当x________时,它的值不小于2;
当x________时,它的值不大于1.
15、已知关于x的不等式x-a<1的解集如图所示,则a的值为________.
16、已知关于x的不等式2x﹣a>﹣3的解集是x>1,则a的值为
.
17、关于x的不等式2x-a≤-3的解集如图所示,则a的值是______
.
18、若方程2x=4的解使关于x的一元一次不等式x
B.a>-3
C.a<3
D.a<-3
19、定义一种新运算“?”,其运算规则为:a?b=-2a+3b.如:1?5=-2×1+3×5=13.
则不等式x?4<0的解集为________.
20、不等式10﹣5x≥0的所有非负整数解的积为 .
三、解答题
21、解下列不等式,并把解集表示在数轴上.
(1)x+2<1;
(2)2x-3≥0;
(3)4x-6
(1)6a+8<7a-6;
(2)8-2x≥5x-6.
23、已知关于x的方程5x-10k=20的解是非负数,求k的取值范围.
24、定义新运算:对于任意有理数a,b,都有a?b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算.例如:2?5=2×(2-5)+1=2×(-3)+1=-6+1=-5.
(1)求(-2)?3的值;
(2)若3?x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.
25、(1)已知关于x,y的方程组的解满足不等式x+y>3,求a的取值范围.
(2)已知关于x,y的方程组的解满足不等式x+y<3,求a的取值范围.
26、已知关于x的方程3(x-2a)+2=2x-a+1的解不适合不等式2x-10>8a,求a的取值范围.
11.4解一元一次不等式(1)-苏科版七年级数学下册
培优训练(解析)
一、选择题
1、有下列不等式:①x+y>-5;②<3;③+≤7;④-x2-3x+4>0.其中属于一元一次不等式的有( )
A.1个
B.2个
C.3个
D.4个
[解析]
根据一元一次不等式的定义判断,①含有两个未知数;②不等式左边分母中含有未知数,不是整式;④是一元二次不等式.只有③符合,故选A.
2、不等式﹣2x<﹣4的解集,在数轴上可表示为( )
A.B.
C.D.
【分析】求出不等式的解集,再根据“大于向右,小于向左,不包括端点用空心,包括端点用实心”的原则将解集在数轴上表示出来.
【解析】解不等式﹣2x<﹣4,得:x>2,
表示在数轴上如图:
故选:C.
3、不等式的解集在数轴上表示如下,正确的是(
)
A.
B.
C.
D.
【答案】B
【分析】先根据不等式的性质:先移项,然后合并同类项再系数化1即可求得不等式的解集,然后在数轴上表示不等式的解集即可.
【详解】不等式,
移项得:,
合并同类项得:
解得:;
在数轴上表示为:
故选:B.
4、不等式x+1≥2x-1的解集在数轴上的表示为( )
A.
B.
C,
D.
[解析]
由x+1≥2x-1得x-2x≥-1-1,则
-x≥-2,从而x≤2.故选B.
5、如果不等式ax>1的解集是x<,那么( )
A.a≥0
B.a≤0
C.a>0
D.a<0
[解析]
根据不等式的基本性质解答,由于不等号的方向发生了改变,所以可判定a为负数.
故选D.
6、一元一次不等式的解集在数轴上表示为(
)
A.B.C.
D.
【答案】B
【分析】先求出不等式的解集,再在数轴上表示出不等式的解集即可.
【详解】-3x-1>2,
-3x>2+1,
-3x>3,
x<-1,
在数轴上表示为:,
故选B.
7、若2x+1为非负数,则x的取值范围是( )
A.x≥1
B.x≥-
C.x>1
D.x>-
[解析]
由题意得2x+1≥0,解得x≥-,故选B.
8、已知(k+3)x|k|﹣2+5<k﹣4是关于x的一元一次不等式,则不等式的解集是( )
A.x<1
B.x<﹣1
C.x<2
D.x>﹣1
【分析】先根据一元一次不等式的概念得出k的值,代入不等式,解之可得.
【解析】∵(k+3)x|k|﹣2+5<k﹣4是关于x的一元一次不等式,
∴k+3≠0且|k|﹣2=1,
解得k=3,
则不等式为6x+5<3﹣4,
解得x<﹣1,
故选:B.
9、阅读理解:我们把称作二阶行列式,规定它的运算法则为=ad-bc,
例如=1×4-3×2=-2.如果>3,那么x的取值范围是( )
A.x>2
B.x<-2
C.x>6
D.x<-6
[解析]
由题意可得2x-(3-x)>3,解得x>2.故选A.
10、若方程组
的解满足3x-4y>0,则k的取值范围是( )
A.k>1
B.k<1
C.k>-1
D.k<-1
[解析]
①-②,得3x-4y=1-k,
由3x-4y>0,得1-k>0,解得k<1.
故选B.
二、填空题
11、若3xm-1-2>1是关于x的一元一次不等式,则m=________.
[答案]
2
[解析]
根据一元一次不等式的概念,知m-1=1,解得m=2.
12、已知(k-3)x|k|-2+5<k-4是关于x的一元一次不等式,求k的值=__________.
解:根据一元一次不等式的定义,有|k|-2=1,且k-3≠0,因此k=-3.
13、不等式2ax>3a的两边都除以2a,写出不等式的解集:
(1)当a>0时,得____________;
(2)当a<0时,得____________.
答案:(1)x> (2)x< [解析]
依据不等式的基本性质2,要注意a的正负.
14、已知代数式-4x+5,当x________时,它的值是正数;当x________时,它的值是负数;
当x________时,它的值不小于2;
当x________时,它的值不大于1.
答案:< > ≤ ≥1
[解析]
根据题意列出不等式,再解不等式.
-4x+5>0,x<;
-4x+5<0,x>;
-4x+52,x≤;
-4x+51,x≥1
15、已知关于x的不等式x-a<1的解集如图所示,则a的值为________.
[答案]
1
[解析]
由图可知x<2.因为解不等式x-a<1得x<1+a,所以1+a=2,解得a=1.
16、已知关于x的不等式2x﹣a>﹣3的解集是x>1,则a的值为
.
【分析】根据解一元一次不等式的方法和题意,可以求得a的值,本题得以解决.
【解析】由2x﹣a>﹣3,得x,
∵不等式2x﹣a>﹣3的解集是x>1,
∴=1,
解得,a=5,
故答案为:5.
17、关于x的不等式2x-a≤-3的解集如图所示,则a的值是______
.
【答案】1
【分析】首先用a表示出不等式的解集,然后解出a.
【详解】∵2x-a≤-3,
∴x≤,
∵x≤-1,
∴a=1.
故答案为1.
18、若方程2x=4的解使关于x的一元一次不等式x
B.a>-3
C.a<3
D.a<-3
[解析]
由2x=4,得x=2,将x=2代入x
故选B.
19、定义一种新运算“?”,其运算规则为:a?b=-2a+3b.如:1?5=-2×1+3×5=13.
则不等式x?4<0的解集为________.
[答案]
x>6
[解析]
根据题意,得x?4=-2x+3×4=-2x+12.因为x?4<0,所以-2x+12<0,解得x>6.
20、不等式10﹣5x≥0的所有非负整数解的积为 .
【分析】先求出不等式的解集,再求出不等式的非负整数解,即可得出答案.
【解析】10﹣5x≥0,
﹣5x≥﹣10,
x≤2,
所以不等式的非负整数解为0,1,2,
0×1×2=0,
故答案为:0.
三、解答题
21、解下列不等式,并把解集表示在数轴上.
(1)x+2<1;
(2)2x-3≥0;
(3)4x-6
(1)不等式两边都减去2;(2)不等式两边都加上3,然后两边都除以2,不等号的方向不变;
(3)不等式两边都减去(x-6),然后两边都除以3,不等号的方向不变.
解:(1)根据不等式的基本性质1,在不等式的两边都减去2,不等号的方向不变,得
x+2-2<1-2,即x<-1,
这个不等式的解集在数轴上的表示如图所示:
(2)根据不等式的基本性质1,在不等式的两边都加上3,得2x-3+3≥0+3,即2x≥3,
根据不等式的基本性质2,不等式的两边同时除以2,不等号的方向不变,得x≥,
这个不等式的解集在数轴上的表示如图所示:
(3)根据不等式的基本性质1,在不等式的两边都减去(x-6),得
4x-6-(x-6)
这个不等式的解集在数轴上的表示如图所示:
22、解下列不等式,并把它们的解集在数轴上表示出来.
(1)6a+8<7a-6;
(2)8-2x≥5x-6.
解:(1)移项,得6a-7a<-6-8,
合并同类项,得-a<-14,
系数化为1,得a>14.
在数轴上表示解集如下:
(2)移项,得-2x-5x≥-6-8,
合并同类项,得-7x≥-14,
系数化为1,得x≤2.
在数轴上表示解集如下:
23、已知关于x的方程5x-10k=20的解是非负数,求k的取值范围.
[解析]
先解关于x的方程,用含k的代数式表示方程的解,再由x是非负数这一条件列出不等式,从而确定k的取值范围.
解:解方程5x-10k=20,得x=2k+4.
因为x是非负数,所以2k+4≥0.
不等式两边都减去4,得2k≥-4,
不等式两边都除以2,得k≥-2.
所以k的取值范围是k≥-2.
24、定义新运算:对于任意有理数a,b,都有a?b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算.例如:2?5=2×(2-5)+1=2×(-3)+1=-6+1=-5.
(1)求(-2)?3的值;
(2)若3?x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.
解:(1)(-2)?3=-2×(-2-3)+1=-2×(-5)+1=10+1=11.
(2)∵3?x<13,∴3(3-x)+1<13,
∴9-3x+1<13,即-3x<3,∴x>-1.
在数轴上表示如图所示:
25、(1)已知关于x,y的方程组的解满足不等式x+y>3,求a的取值范围.
(2)已知关于x,y的方程组的解满足不等式x+y<3,求a的取值范围.
解:(1)
①+②,得3x=6a+3,即x=2a+1.
将x=2a+1代入①,得2a+1-y=3a+3,解得y=-a-2.
所以方程组的解为
因为方程组的解满足不等式x+y>3,
所以2a+1+(-a-2)>3,
解得a>4.
(2)
①+②,得3x=6a+3,解得x=2a+1.
将x=2a+1代入①,得y=2a-2.
因为x+y<3,所以2a+1+2a-2<3,
即4a<4,
所以a<1.
26、已知关于x的方程3(x-2a)+2=2x-a+1的解不适合不等式2x-10>8a,求a的取值范围.
解:方程3(x-2a)+2=2x-a+1的解为x=5a-1,
不等式2x-10>8a的解集是x>4a+5.
根据题意,得5a-1≤4a+5,
∴
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
