2020-2021学年七年级数学人教版(五四制)下册第18章全等三角形单元练习(word解析版)
文档属性
| 名称 | 2020-2021学年七年级数学人教版(五四制)下册第18章全等三角形单元练习(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 262.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 00:00:00 | ||
图片预览


文档简介
第18章
全等三角形
一、选择题(本题共计8小题,每题3分,共计24分,)
1.不能判定两个直角三角形全等的条件是( )
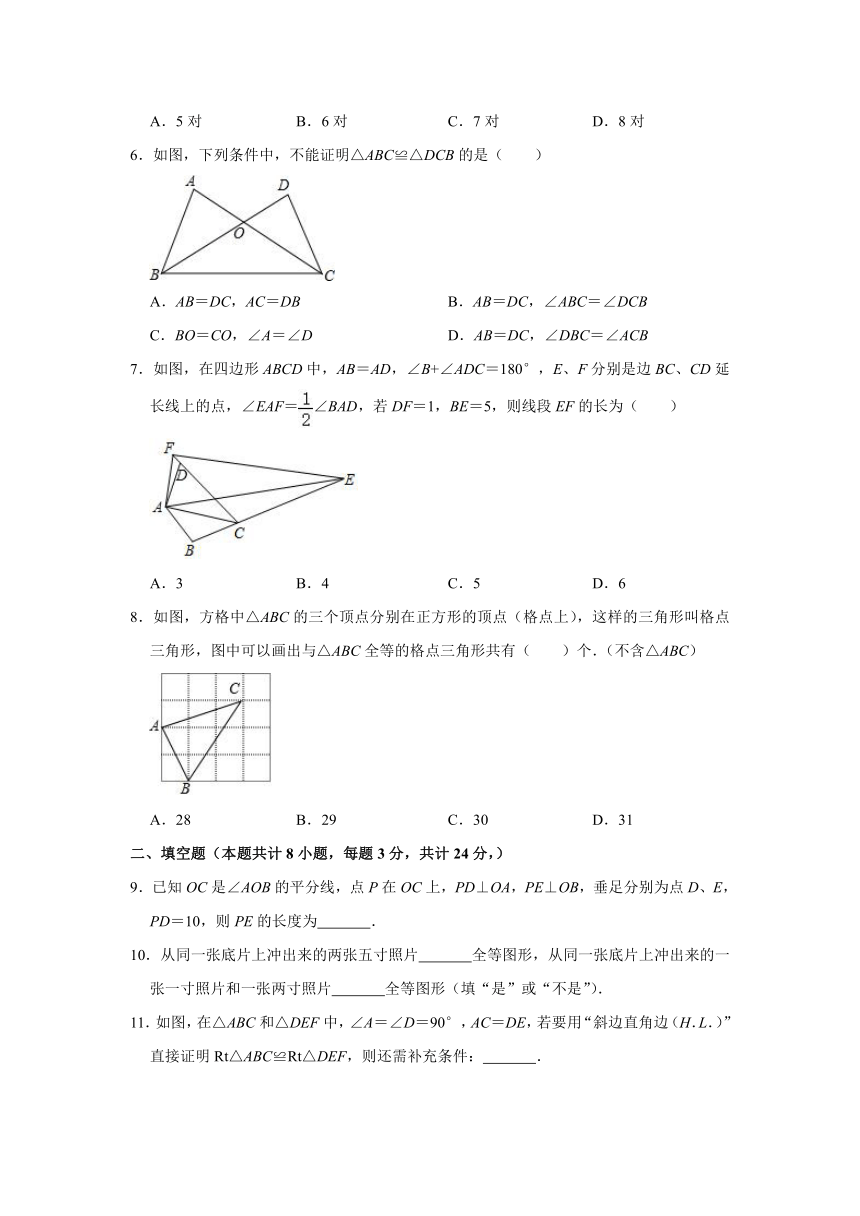
A.两个锐角对应相等
B.两条直角边对应相等
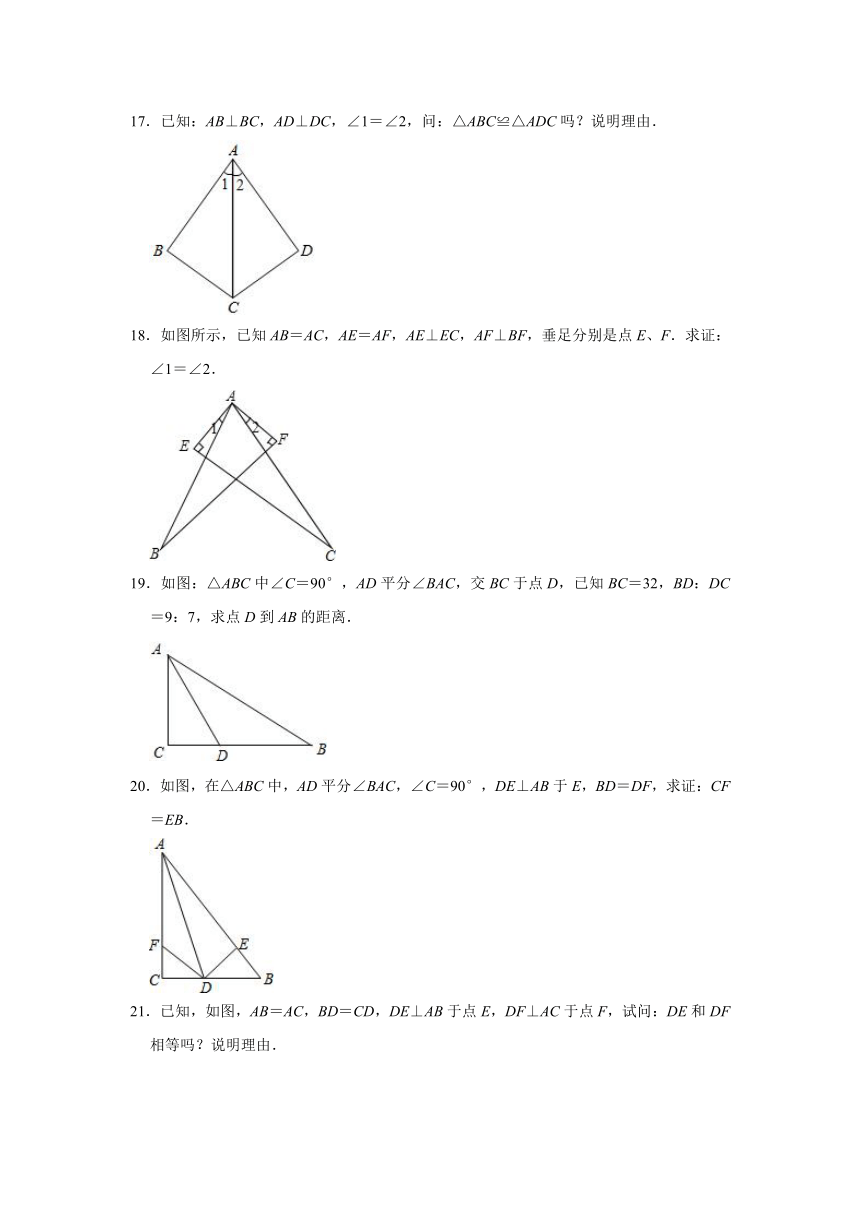
C.斜边和一锐角对应相等
D.斜边和一条直角边对应相等
2.如图,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,则DE的长等于( )
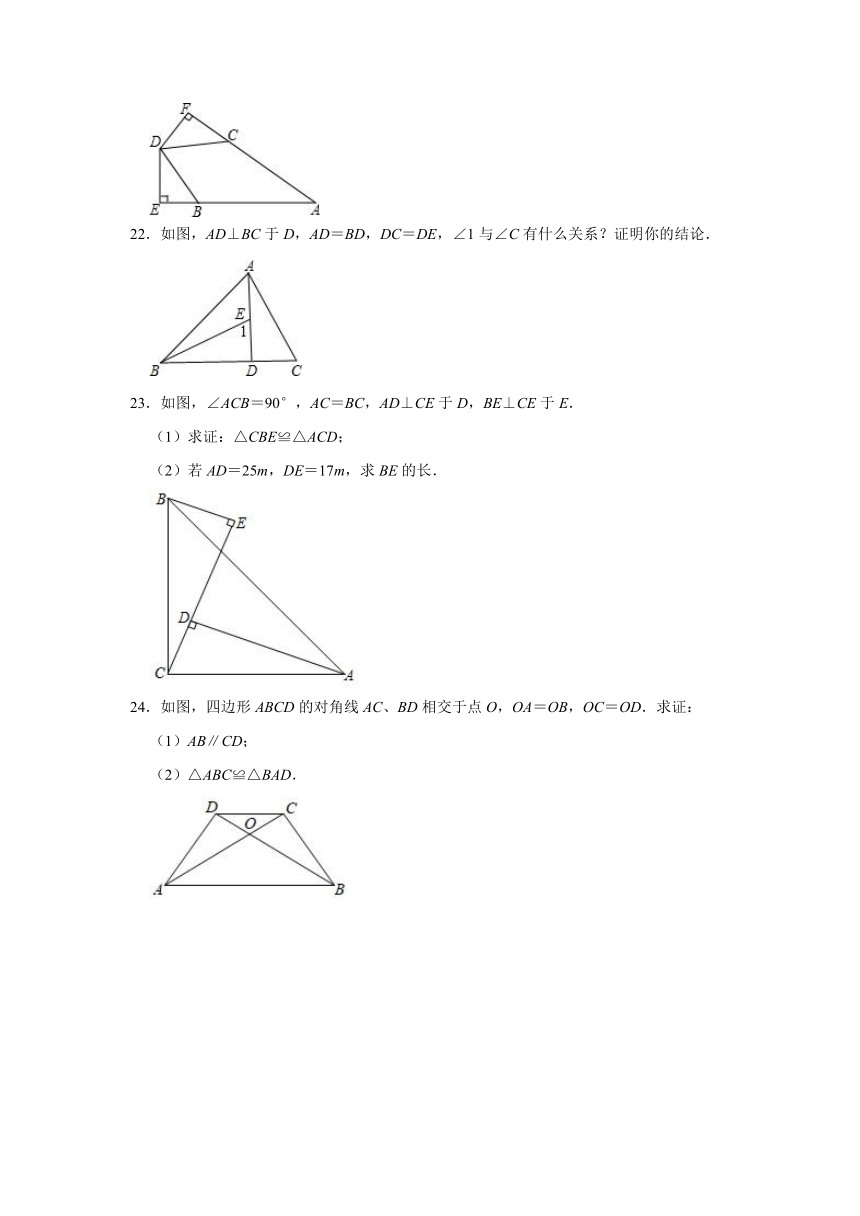
A.DC
B.BC
C.AB
D.AE+AC
3.如图,P是△ABC的三条角平分线的交点,连接PA、PB、PC,若△PAB、△PBC、△PAC的面积分别为S1、S2、S3,则S1( )S2+S3.
A.>
B.=
C.<
D.无法确定
4.下列条件不能证明两个直角三角形全等的是( )
A.斜边和一直角边对应相等
B.一直角边和一角对应相等
C.两条直角边对应相等
D.斜边和一锐角对应相等
5.如图,已知,AC∥BD,AB∥CD,AD与BC交于点O,AE⊥BC于点E,DF⊥BC于点F,那么图中全等的三角形有( )
A.5对
B.6对
C.7对
D.8对
6.如图,下列条件中,不能证明△ABC≌△DCB的是( )
A.AB=DC,AC=DB
B.AB=DC,∠ABC=∠DCB
C.BO=CO,∠A=∠D
D.AB=DC,∠DBC=∠ACB
7.如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,∠EAF=∠BAD,若DF=1,BE=5,则线段EF的长为( )
A.3
B.4
C.5
D.6
8.如图,方格中△ABC的三个顶点分别在正方形的顶点(格点上),这样的三角形叫格点三角形,图中可以画出与△ABC全等的格点三角形共有( )个.(不含△ABC)
A.28
B.29
C.30
D.31
二、填空题(本题共计8小题,每题3分,共计24分,)
9.已知OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为点D、E,PD=10,则PE的长度为
.
10.从同一张底片上冲出来的两张五寸照片
全等图形,从同一张底片上冲出来的一张一寸照片和一张两寸照片
全等图形(填“是”或“不是”).
11.如图,在△ABC和△DEF中,∠A=∠D=90°,AC=DE,若要用“斜边直角边(H.L.)”直接证明Rt△ABC≌Rt△DEF,则还需补充条件:
.
12.如图,△ABC≌△EDF,DF=BC,AB=ED,AF=20,EC=10,则AE的长是
.
13.如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=12cm,BD=8cm,则点D到AB的距离为
cm.
14.如图,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,只添加一个条件使△ABE≌△ACD,添加的条件是:
.
15.如图,已知AC=BD,要使△ABC≌△DCB,只需增加的一个条件是
.
16.如图,∠B=∠E=90°,AC=DF,BF=EC,则除条件以外,相等的线段还有
.
三、解答题(本题共计8小题,共计72分,)
17.已知:AB⊥BC,AD⊥DC,∠1=∠2,问:△ABC≌△ADC吗?说明理由.
18.如图所示,已知AB=AC,AE=AF,AE⊥EC,AF⊥BF,垂足分别是点E、F.求证:∠1=∠2.
19.如图:△ABC中∠C=90°,AD平分∠BAC,交BC于点D,已知BC=32,BD:DC=9:7,求点D到AB的距离.
20.如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于E,BD=DF,求证:CF=EB.
21.已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,试问:DE和DF相等吗?说明理由.
22.如图,AD⊥BC于D,AD=BD,DC=DE,∠1与∠C有什么关系?证明你的结论.
23.如图,∠ACB=90°,AC=BC,AD⊥CE于D,BE⊥CE于E.
(1)求证:△CBE≌△ACD;
(2)若AD=25m,DE=17m,求BE的长.
24.如图,四边形ABCD的对角线AC、BD相交于点O,OA=OB,OC=OD.求证:
(1)AB∥CD;
(2)△ABC≌△BAD.
参考答案与试题解析
一、选择题(本题共计8小题,每题3分,共计24分,)
1.不能判定两个直角三角形全等的条件是( )
A.两个锐角对应相等
B.两条直角边对应相等
C.斜边和一锐角对应相等
D.斜边和一条直角边对应相等
【分析】直角三角形全等的判定方法:HL,SAS,ASA,SSS,AAS,做题时要结合已知条件与全等的判定方法逐一验证.
【解答】解:A、全等三角形的判定必须有边的参与,故本选项错误,符合题意;
B、符合判定SAS,故本选项正确,不符合题意;
C、符合判定AAS,故本选项正确,不符合题意;
D、符合判定HL,故本选项正确,不符合题意.
故选:A.
2.如图,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,则DE的长等于( )
A.DC
B.BC
C.AB
D.AE+AC
【分析】通过角的计算可得出∠B=∠D、∠BCA=∠DCE,再结合AC=CE即可证出△ABC≌△EDC(AAS),由此即可得出DE=BA,此题得解.
【解答】解:∵∠1=∠2,∠AFD=∠CFB,∠1+∠AFD+∠D=180°=∠2+∠CFB+∠B,
∴∠B=∠D.
∵∠2=∠3,∠DCE=∠DCA+∠3,∠BCA=∠2+∠DCA,
∴∠BCA=∠DCE.
在△ABC和△EDC中,,
∴△ABC≌△EDC(AAS),
∴DE=BA.
故选:C.
3.如图,P是△ABC的三条角平分线的交点,连接PA、PB、PC,若△PAB、△PBC、△PAC的面积分别为S1、S2、S3,则S1( )S2+S3.
A.>
B.=
C.<
D.无法确定
【分析】过P点作PD⊥AB于D,PE⊥AC于E,PF⊥BC于F,如图,利用角平分线的性质得到PD=PE=PF,再利用三角形面积公式得到S1=?AB?PD,S2=?BC?PF,S3=?AC?PE,然后根据三角形三边的关系求解.
【解答】解:过P点作PD⊥AB于D,PE⊥AC于E,PF⊥BC于F,如图,
∵P是△ABC的三条角平分线的交点,
∴PD=PE=PF,
∵S1=?AB?PD,S2=?BC?PF,S3=?AC?PE,
∴S2+S3=?(AC+BC)?PD,
∵AB<AC+BC,
∴S1<S2+S3.
故选:C.
4.下列条件不能证明两个直角三角形全等的是( )
A.斜边和一直角边对应相等
B.一直角边和一角对应相等
C.两条直角边对应相等
D.斜边和一锐角对应相等
【分析】此题需用排除法,对各个选项进行分析从而确定答案.
【解答】A、符合HL,正确;
B、仅知道一条直角边和一角也不能确定确定其它各边的长,从而不能判定两直角三角形相等,错误;
C、知道两直角边,可以求得第三边.从而利用SSS,正确;
D、知道斜边和一锐角,可以推出另一角的度数.从而可以确定其它边,正确.
故选:B.
5.如图,已知,AC∥BD,AB∥CD,AD与BC交于点O,AE⊥BC于点E,DF⊥BC于点F,那么图中全等的三角形有( )
A.5对
B.6对
C.7对
D.8对
【分析】根据能完全重合的三角形是全等三角形,可得答案.
【解答】解:AB∥CD,AC∥BD,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,
那么图中全等的三角形有:△ACE≌△DBF,△AEO≌△DFO,△ACO≌△DBF,△AOB≌△DOC,△AEB≌△DFC,△ACB≌△DBC,△ACD≌△DBA,共有7对,
故选:C.
6.如图,下列条件中,不能证明△ABC≌△DCB的是( )
A.AB=DC,AC=DB
B.AB=DC,∠ABC=∠DCB
C.BO=CO,∠A=∠D
D.AB=DC,∠DBC=∠ACB
【分析】本题要判定△ABC≌△DCB,已知BC是公共边,具备了一组边对应相等.所以由全等三角形的判定定理作出正确的判断即可.
【解答】解:根据题意知,BC边为公共边.
A、由“SSS”可以判定△ABC≌△DCB,故本选项错误;
B、由“SAS”可以判定△ABC≌△DCB,故本选项错误;
C、由BO=CO可以推知∠ACB=∠DBC,则由“AAS”可以判定△ABC≌△DCB,故本选项错误;
D、由“SSA”不能判定△ABC≌△DCB,故本选项正确.
故选:D.
7.如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,∠EAF=∠BAD,若DF=1,BE=5,则线段EF的长为( )
A.3
B.4
C.5
D.6
【分析】根据全等三角形的判定和性质解答.
【解答】解:在BE上截取BG=DF,
∵∠B+∠ADC=180°,∠ADC+∠ADF=180°,
∴∠B=∠ADF,
在△ADF与△ABG中
,
∴△ADF≌△ABG(SAS),
∴AG=AF,∠FAD=∠GAB,
∵∠EAF=∠BAD,
∴∠FAE=∠GAE,
在△AEG与△AEF中
,
∴△AEG≌△AEF(SAS)
∴EF=EG=BE﹣BG=BE﹣DF=4.
故选:B.
8.如图,方格中△ABC的三个顶点分别在正方形的顶点(格点上),这样的三角形叫格点三角形,图中可以画出与△ABC全等的格点三角形共有( )个.(不含△ABC)
A.28
B.29
C.30
D.31
【分析】当点B在下面时,根据平移,对称,可得与△ABC全等的三角形有8个,包括△ABC,当点B在其它3条边上时,有3×8=24(个)三角形与△ABC全等,由此即可判断.
【解答】解:当点B在下面时,根据平移,对称,可得与△ABC全等的三角形有8个,包括△ABC,
当点B在其它3条边上时,有3×8=24(个)三角形与△ABC全等,
∴一共有:8+24﹣1=31(个)三角形与△ABC全等,
故选:D.
二、填空题(本题共计8小题,每题3分,共计24分,)
9.已知OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为点D、E,PD=10,则PE的长度为 10 .
【分析】根据角平分线上的点到角的两边距离相等可得PE=PD.
【解答】解:∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PE=PD=10.
故答案为:10.
10.从同一张底片上冲出来的两张五寸照片 是 全等图形,从同一张底片上冲出来的一张一寸照片和一张两寸照片 不是 全等图形(填“是”或“不是”).
【分析】根据能够完全重合的两个图形叫做全等形,图形重合的是全等形,不重合的不是全等形,进行判断.
【解答】解:由全等形的概念可知:从同一张底片上冲出来的两张五寸照片是全等图形,
由同一张底片冲洗出来的一寸照片和二寸照片,大小不一样,所以不是全等图形.
故答案为:是,不是.
11.如图,在△ABC和△DEF中,∠A=∠D=90°,AC=DE,若要用“斜边直角边(H.L.)”直接证明Rt△ABC≌Rt△DEF,则还需补充条件: BC=EF .
【分析】此题是一道开放型题目,根据直角三角形的全等判定解答即可.
【解答】解:在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
故答案为:BC=EF
12.如图,△ABC≌△EDF,DF=BC,AB=ED,AF=20,EC=10,则AE的长是 5 .
【分析】根据全等三角形对应边相等可得AC=EF,然后求出AE=CF,代入数据计算即可得解.
【解答】解:∵△ABC≌△EDF,
∴AC=EF,
∴AC﹣CE=EF﹣CE,
即AE=CF,
∵AF=20,EC=10,
∴AE=×(20﹣10)=5.
故答案为:5.
13.如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=12cm,BD=8cm,则点D到AB的距离为 4 cm.
【分析】先过点D作DE⊥AB于点E,根据BC=12cm,BD=8cm求出DC的长,由∠C=90°可知,DC⊥AC,再根据AD平分∠BAC可得出DE=DC,故可得出结论.
【解答】解:先过点D作DE⊥AB于点E,
∵BC=12cm,BD=8cm,
∴DC=12﹣8=4cm,
∵∠C=90°,
∴DC⊥AC,
∵AD平分∠BAC,
∴DE=DC=4cm.
故答案为:4.
14.如图,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,只添加一个条件使△ABE≌△ACD,添加的条件是: ∠B=∠C .
【分析】添加条件是∠B=∠C,根据全等三角形的判定定理ASA推出即可,此题是一道开放型的题目,答案不唯一.
【解答】解:∠B=∠C,
理由是:∵在△ABE和△ACD中
∴△ABE≌△ACD(ASA),
故答案为:∠B=∠C.
15.如图,已知AC=BD,要使△ABC≌△DCB,只需增加的一个条件是 ∠ACB=∠DBC(或AB=CD) .
【分析】要使△ABC≌△DCB,根据三角形全等的判定方法添加适合的条件即可.
【解答】解:∵AC=BD,BC=BC,
∴可添加∠ACB=∠DBC或AB=CD分别利用SAS,SSS判定△ABC≌△DCB.
故答案为:∠ACB=∠DBC(或AB=CD).
16.如图,∠B=∠E=90°,AC=DF,BF=EC,则除条件以外,相等的线段还有 AB=DE,BC=EF,BF=CE. .
【分析】利用HL定理证明△ABC≌△DEF,然后根据全等三角形的对应边相等即可解答.
【解答】解:在直角△ABC和直角△DEF中,
,
∴△ABC≌△DEF,
∴AB=DE,BC=EF,则BF=CE.
故答案是:AB=DE,BC=EF,BF=CE.
三、解答题(本题共计8小题,共计72分,)
17.已知:AB⊥BC,AD⊥DC,∠1=∠2,问:△ABC≌△ADC吗?说明理由.
【分析】根据全等三角形的判定定理AAS进行证明.
【解答】解:△ABC≌△ADC.理由如下:
∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°.
在△ABC与△ADC中,
,
∴△ABC≌△ADC(AAS).
18.如图所示,已知AB=AC,AE=AF,AE⊥EC,AF⊥BF,垂足分别是点E、F.求证:∠1=∠2.
【分析】根据HL证明Rt△AEC与Rt△AFB全等,再利用等式的性质解答即可.
【解答】证明:∵AE⊥EC,AF⊥BF,
∴△AEC是Rt△,△AFB是Rt△,
在Rt△AEC与Rt△AFB中,
,
∴Rt△AEC≌Rt△AFB(HL),
∴∠EAC=∠FAB,
∴∠EAC﹣∠BAC=∠FAB﹣∠BAC,
即∠1=∠2.
19.如图:△ABC中∠C=90°,AD平分∠BAC,交BC于点D,已知BC=32,BD:DC=9:7,求点D到AB的距离.
【分析】先由BC=32,BD:DC=9:7计算出DC=14,再由∠C=90°,得到点D到AC的距离等于14,然后根据角平分线的性质求解.
【解答】解:∵BC=32,BD:DC=9:7,
∴DC=14,
∵∠C=90°,
∴点D到AC的距离等于14,
∵AD平分∠BAC,
∴点D到AB的距离等于14.
20.如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于E,BD=DF,求证:CF=EB.
【分析】根据角平分线的性质“角平分线上的点到角的两边的距离相等”,可得点D到AB的距离=点D到AC的距离即DE=CD,再根据HL证明Rt△CDF≌Rt△EBD,从而得出CF=EB.
【解答】证明:∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在△CDF与△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
21.已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,试问:DE和DF相等吗?说明理由.
【分析】连接AD,易证△ACD≌△ABD,根据全等三角形对应角相等的性质可得∠EAD=∠FAD,再根据∠AED=∠AFD,AD=AD,即可证明△ADE≌△ADF,根据全等三角形对应边相等的性质可得DE=DF.
【解答】证明:
连接AD,在△ACD和△ABD中,,
∴ACD≌△ABD(SSS),
∵DE⊥AE,DF⊥AF,
∴∠AED=∠AFD=90°,
∴在△ADE和△ADF中,,
∴△ADE≌△ADF,
∴DE=DF.
22.如图,AD⊥BC于D,AD=BD,DC=DE,∠1与∠C有什么关系?证明你的结论.
【分析】相等,可通过证明三角形BED和ACD全等来实现,已知了一组直角和两组对应边相等因此可证得两三角形全等,也就得出了∠C=∠1的结论.
【解答】解:∠C=∠1,理由如下:
∵AD⊥BC,
∴∠ADC=∠BDE=90°.
又∵DC=DE,AD=BD,
∴△ADC≌△BDE.
∴∠C=∠1.
23.如图,∠ACB=90°,AC=BC,AD⊥CE于D,BE⊥CE于E.
(1)求证:△CBE≌△ACD;
(2)若AD=25m,DE=17m,求BE的长.
【分析】(1)先证∠CBE=∠ACD,再由AAS证明△CBE≌△ACD即可;
(2)根据全等三角形的性质得出BE=CD,CE=AD=25m,即可推出答案.
【解答】(1)证明:∵AD⊥CE于D,BE⊥CE于E,
∴∠E=∠CDA=∠ACB=90°,
∴∠BCE+∠ACD=90°,∠BCE+∠CBE=90°,
∴∠CBE=∠ACD,
在△CBE和△ACD中,
,
∴△CBE≌△ACD(AAS);
(2)解:∵△CBE≌△ACD,
∴BE=CD,AD=CE=AD=25m,
∴BE=CD=CE﹣DE=25﹣17=8(m),
即BE的长为8m.
24.如图,四边形ABCD的对角线AC、BD相交于点O,OA=OB,OC=OD.求证:
(1)AB∥CD;
(2)△ABC≌△BAD.
【分析】(1)根据等腰三角形的性质得出∠OAB=∠OBA,∠OCD=∠ODC,求出∠OAB=∠OCD,根据平行线的判定推出即可;
(2)求出AC=BD,根据SAS推出即可.
【解答】(1)证明:∵OA=OB,OC=OD,
∴∠OAB=∠OBA,∠OCD=∠ODC,
∵∠COD=∠AOB,∠OAB+∠OBA+∠AOB=180°,∠OCD+∠ODC+∠COD=180°,
∴∠OAB=∠OBA=∠OCD=∠ODC,
即∠OAB=∠OCD,
∴AB∥CD;
(2)∵OA=OB,OC=OD,
∴AC=BD,
在△ABC和△BAD中,
,
∴△ABC≌△BAD(SAS).
全等三角形
一、选择题(本题共计8小题,每题3分,共计24分,)
1.不能判定两个直角三角形全等的条件是( )
A.两个锐角对应相等
B.两条直角边对应相等
C.斜边和一锐角对应相等
D.斜边和一条直角边对应相等
2.如图,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,则DE的长等于( )
A.DC
B.BC
C.AB
D.AE+AC
3.如图,P是△ABC的三条角平分线的交点,连接PA、PB、PC,若△PAB、△PBC、△PAC的面积分别为S1、S2、S3,则S1( )S2+S3.
A.>
B.=
C.<
D.无法确定
4.下列条件不能证明两个直角三角形全等的是( )
A.斜边和一直角边对应相等
B.一直角边和一角对应相等
C.两条直角边对应相等
D.斜边和一锐角对应相等
5.如图,已知,AC∥BD,AB∥CD,AD与BC交于点O,AE⊥BC于点E,DF⊥BC于点F,那么图中全等的三角形有( )
A.5对
B.6对
C.7对
D.8对
6.如图,下列条件中,不能证明△ABC≌△DCB的是( )
A.AB=DC,AC=DB
B.AB=DC,∠ABC=∠DCB
C.BO=CO,∠A=∠D
D.AB=DC,∠DBC=∠ACB
7.如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,∠EAF=∠BAD,若DF=1,BE=5,则线段EF的长为( )
A.3
B.4
C.5
D.6
8.如图,方格中△ABC的三个顶点分别在正方形的顶点(格点上),这样的三角形叫格点三角形,图中可以画出与△ABC全等的格点三角形共有( )个.(不含△ABC)
A.28
B.29
C.30
D.31
二、填空题(本题共计8小题,每题3分,共计24分,)
9.已知OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为点D、E,PD=10,则PE的长度为
.
10.从同一张底片上冲出来的两张五寸照片
全等图形,从同一张底片上冲出来的一张一寸照片和一张两寸照片
全等图形(填“是”或“不是”).
11.如图,在△ABC和△DEF中,∠A=∠D=90°,AC=DE,若要用“斜边直角边(H.L.)”直接证明Rt△ABC≌Rt△DEF,则还需补充条件:
.
12.如图,△ABC≌△EDF,DF=BC,AB=ED,AF=20,EC=10,则AE的长是
.
13.如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=12cm,BD=8cm,则点D到AB的距离为
cm.
14.如图,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,只添加一个条件使△ABE≌△ACD,添加的条件是:
.
15.如图,已知AC=BD,要使△ABC≌△DCB,只需增加的一个条件是
.
16.如图,∠B=∠E=90°,AC=DF,BF=EC,则除条件以外,相等的线段还有
.
三、解答题(本题共计8小题,共计72分,)
17.已知:AB⊥BC,AD⊥DC,∠1=∠2,问:△ABC≌△ADC吗?说明理由.
18.如图所示,已知AB=AC,AE=AF,AE⊥EC,AF⊥BF,垂足分别是点E、F.求证:∠1=∠2.
19.如图:△ABC中∠C=90°,AD平分∠BAC,交BC于点D,已知BC=32,BD:DC=9:7,求点D到AB的距离.
20.如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于E,BD=DF,求证:CF=EB.
21.已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,试问:DE和DF相等吗?说明理由.
22.如图,AD⊥BC于D,AD=BD,DC=DE,∠1与∠C有什么关系?证明你的结论.
23.如图,∠ACB=90°,AC=BC,AD⊥CE于D,BE⊥CE于E.
(1)求证:△CBE≌△ACD;
(2)若AD=25m,DE=17m,求BE的长.
24.如图,四边形ABCD的对角线AC、BD相交于点O,OA=OB,OC=OD.求证:
(1)AB∥CD;
(2)△ABC≌△BAD.
参考答案与试题解析
一、选择题(本题共计8小题,每题3分,共计24分,)
1.不能判定两个直角三角形全等的条件是( )
A.两个锐角对应相等
B.两条直角边对应相等
C.斜边和一锐角对应相等
D.斜边和一条直角边对应相等
【分析】直角三角形全等的判定方法:HL,SAS,ASA,SSS,AAS,做题时要结合已知条件与全等的判定方法逐一验证.
【解答】解:A、全等三角形的判定必须有边的参与,故本选项错误,符合题意;
B、符合判定SAS,故本选项正确,不符合题意;
C、符合判定AAS,故本选项正确,不符合题意;
D、符合判定HL,故本选项正确,不符合题意.
故选:A.
2.如图,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,则DE的长等于( )
A.DC
B.BC
C.AB
D.AE+AC
【分析】通过角的计算可得出∠B=∠D、∠BCA=∠DCE,再结合AC=CE即可证出△ABC≌△EDC(AAS),由此即可得出DE=BA,此题得解.
【解答】解:∵∠1=∠2,∠AFD=∠CFB,∠1+∠AFD+∠D=180°=∠2+∠CFB+∠B,
∴∠B=∠D.
∵∠2=∠3,∠DCE=∠DCA+∠3,∠BCA=∠2+∠DCA,
∴∠BCA=∠DCE.
在△ABC和△EDC中,,
∴△ABC≌△EDC(AAS),
∴DE=BA.
故选:C.
3.如图,P是△ABC的三条角平分线的交点,连接PA、PB、PC,若△PAB、△PBC、△PAC的面积分别为S1、S2、S3,则S1( )S2+S3.
A.>
B.=
C.<
D.无法确定
【分析】过P点作PD⊥AB于D,PE⊥AC于E,PF⊥BC于F,如图,利用角平分线的性质得到PD=PE=PF,再利用三角形面积公式得到S1=?AB?PD,S2=?BC?PF,S3=?AC?PE,然后根据三角形三边的关系求解.
【解答】解:过P点作PD⊥AB于D,PE⊥AC于E,PF⊥BC于F,如图,
∵P是△ABC的三条角平分线的交点,
∴PD=PE=PF,
∵S1=?AB?PD,S2=?BC?PF,S3=?AC?PE,
∴S2+S3=?(AC+BC)?PD,
∵AB<AC+BC,
∴S1<S2+S3.
故选:C.
4.下列条件不能证明两个直角三角形全等的是( )
A.斜边和一直角边对应相等
B.一直角边和一角对应相等
C.两条直角边对应相等
D.斜边和一锐角对应相等
【分析】此题需用排除法,对各个选项进行分析从而确定答案.
【解答】A、符合HL,正确;
B、仅知道一条直角边和一角也不能确定确定其它各边的长,从而不能判定两直角三角形相等,错误;
C、知道两直角边,可以求得第三边.从而利用SSS,正确;
D、知道斜边和一锐角,可以推出另一角的度数.从而可以确定其它边,正确.
故选:B.
5.如图,已知,AC∥BD,AB∥CD,AD与BC交于点O,AE⊥BC于点E,DF⊥BC于点F,那么图中全等的三角形有( )
A.5对
B.6对
C.7对
D.8对
【分析】根据能完全重合的三角形是全等三角形,可得答案.
【解答】解:AB∥CD,AC∥BD,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,
那么图中全等的三角形有:△ACE≌△DBF,△AEO≌△DFO,△ACO≌△DBF,△AOB≌△DOC,△AEB≌△DFC,△ACB≌△DBC,△ACD≌△DBA,共有7对,
故选:C.
6.如图,下列条件中,不能证明△ABC≌△DCB的是( )
A.AB=DC,AC=DB
B.AB=DC,∠ABC=∠DCB
C.BO=CO,∠A=∠D
D.AB=DC,∠DBC=∠ACB
【分析】本题要判定△ABC≌△DCB,已知BC是公共边,具备了一组边对应相等.所以由全等三角形的判定定理作出正确的判断即可.
【解答】解:根据题意知,BC边为公共边.
A、由“SSS”可以判定△ABC≌△DCB,故本选项错误;
B、由“SAS”可以判定△ABC≌△DCB,故本选项错误;
C、由BO=CO可以推知∠ACB=∠DBC,则由“AAS”可以判定△ABC≌△DCB,故本选项错误;
D、由“SSA”不能判定△ABC≌△DCB,故本选项正确.
故选:D.
7.如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,∠EAF=∠BAD,若DF=1,BE=5,则线段EF的长为( )
A.3
B.4
C.5
D.6
【分析】根据全等三角形的判定和性质解答.
【解答】解:在BE上截取BG=DF,
∵∠B+∠ADC=180°,∠ADC+∠ADF=180°,
∴∠B=∠ADF,
在△ADF与△ABG中
,
∴△ADF≌△ABG(SAS),
∴AG=AF,∠FAD=∠GAB,
∵∠EAF=∠BAD,
∴∠FAE=∠GAE,
在△AEG与△AEF中
,
∴△AEG≌△AEF(SAS)
∴EF=EG=BE﹣BG=BE﹣DF=4.
故选:B.
8.如图,方格中△ABC的三个顶点分别在正方形的顶点(格点上),这样的三角形叫格点三角形,图中可以画出与△ABC全等的格点三角形共有( )个.(不含△ABC)
A.28
B.29
C.30
D.31
【分析】当点B在下面时,根据平移,对称,可得与△ABC全等的三角形有8个,包括△ABC,当点B在其它3条边上时,有3×8=24(个)三角形与△ABC全等,由此即可判断.
【解答】解:当点B在下面时,根据平移,对称,可得与△ABC全等的三角形有8个,包括△ABC,
当点B在其它3条边上时,有3×8=24(个)三角形与△ABC全等,
∴一共有:8+24﹣1=31(个)三角形与△ABC全等,
故选:D.
二、填空题(本题共计8小题,每题3分,共计24分,)
9.已知OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为点D、E,PD=10,则PE的长度为 10 .
【分析】根据角平分线上的点到角的两边距离相等可得PE=PD.
【解答】解:∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PE=PD=10.
故答案为:10.
10.从同一张底片上冲出来的两张五寸照片 是 全等图形,从同一张底片上冲出来的一张一寸照片和一张两寸照片 不是 全等图形(填“是”或“不是”).
【分析】根据能够完全重合的两个图形叫做全等形,图形重合的是全等形,不重合的不是全等形,进行判断.
【解答】解:由全等形的概念可知:从同一张底片上冲出来的两张五寸照片是全等图形,
由同一张底片冲洗出来的一寸照片和二寸照片,大小不一样,所以不是全等图形.
故答案为:是,不是.
11.如图,在△ABC和△DEF中,∠A=∠D=90°,AC=DE,若要用“斜边直角边(H.L.)”直接证明Rt△ABC≌Rt△DEF,则还需补充条件: BC=EF .
【分析】此题是一道开放型题目,根据直角三角形的全等判定解答即可.
【解答】解:在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
故答案为:BC=EF
12.如图,△ABC≌△EDF,DF=BC,AB=ED,AF=20,EC=10,则AE的长是 5 .
【分析】根据全等三角形对应边相等可得AC=EF,然后求出AE=CF,代入数据计算即可得解.
【解答】解:∵△ABC≌△EDF,
∴AC=EF,
∴AC﹣CE=EF﹣CE,
即AE=CF,
∵AF=20,EC=10,
∴AE=×(20﹣10)=5.
故答案为:5.
13.如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=12cm,BD=8cm,则点D到AB的距离为 4 cm.
【分析】先过点D作DE⊥AB于点E,根据BC=12cm,BD=8cm求出DC的长,由∠C=90°可知,DC⊥AC,再根据AD平分∠BAC可得出DE=DC,故可得出结论.
【解答】解:先过点D作DE⊥AB于点E,
∵BC=12cm,BD=8cm,
∴DC=12﹣8=4cm,
∵∠C=90°,
∴DC⊥AC,
∵AD平分∠BAC,
∴DE=DC=4cm.
故答案为:4.
14.如图,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,只添加一个条件使△ABE≌△ACD,添加的条件是: ∠B=∠C .
【分析】添加条件是∠B=∠C,根据全等三角形的判定定理ASA推出即可,此题是一道开放型的题目,答案不唯一.
【解答】解:∠B=∠C,
理由是:∵在△ABE和△ACD中
∴△ABE≌△ACD(ASA),
故答案为:∠B=∠C.
15.如图,已知AC=BD,要使△ABC≌△DCB,只需增加的一个条件是 ∠ACB=∠DBC(或AB=CD) .
【分析】要使△ABC≌△DCB,根据三角形全等的判定方法添加适合的条件即可.
【解答】解:∵AC=BD,BC=BC,
∴可添加∠ACB=∠DBC或AB=CD分别利用SAS,SSS判定△ABC≌△DCB.
故答案为:∠ACB=∠DBC(或AB=CD).
16.如图,∠B=∠E=90°,AC=DF,BF=EC,则除条件以外,相等的线段还有 AB=DE,BC=EF,BF=CE. .
【分析】利用HL定理证明△ABC≌△DEF,然后根据全等三角形的对应边相等即可解答.
【解答】解:在直角△ABC和直角△DEF中,
,
∴△ABC≌△DEF,
∴AB=DE,BC=EF,则BF=CE.
故答案是:AB=DE,BC=EF,BF=CE.
三、解答题(本题共计8小题,共计72分,)
17.已知:AB⊥BC,AD⊥DC,∠1=∠2,问:△ABC≌△ADC吗?说明理由.
【分析】根据全等三角形的判定定理AAS进行证明.
【解答】解:△ABC≌△ADC.理由如下:
∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°.
在△ABC与△ADC中,
,
∴△ABC≌△ADC(AAS).
18.如图所示,已知AB=AC,AE=AF,AE⊥EC,AF⊥BF,垂足分别是点E、F.求证:∠1=∠2.
【分析】根据HL证明Rt△AEC与Rt△AFB全等,再利用等式的性质解答即可.
【解答】证明:∵AE⊥EC,AF⊥BF,
∴△AEC是Rt△,△AFB是Rt△,
在Rt△AEC与Rt△AFB中,
,
∴Rt△AEC≌Rt△AFB(HL),
∴∠EAC=∠FAB,
∴∠EAC﹣∠BAC=∠FAB﹣∠BAC,
即∠1=∠2.
19.如图:△ABC中∠C=90°,AD平分∠BAC,交BC于点D,已知BC=32,BD:DC=9:7,求点D到AB的距离.
【分析】先由BC=32,BD:DC=9:7计算出DC=14,再由∠C=90°,得到点D到AC的距离等于14,然后根据角平分线的性质求解.
【解答】解:∵BC=32,BD:DC=9:7,
∴DC=14,
∵∠C=90°,
∴点D到AC的距离等于14,
∵AD平分∠BAC,
∴点D到AB的距离等于14.
20.如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于E,BD=DF,求证:CF=EB.
【分析】根据角平分线的性质“角平分线上的点到角的两边的距离相等”,可得点D到AB的距离=点D到AC的距离即DE=CD,再根据HL证明Rt△CDF≌Rt△EBD,从而得出CF=EB.
【解答】证明:∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在△CDF与△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
21.已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,试问:DE和DF相等吗?说明理由.
【分析】连接AD,易证△ACD≌△ABD,根据全等三角形对应角相等的性质可得∠EAD=∠FAD,再根据∠AED=∠AFD,AD=AD,即可证明△ADE≌△ADF,根据全等三角形对应边相等的性质可得DE=DF.
【解答】证明:
连接AD,在△ACD和△ABD中,,
∴ACD≌△ABD(SSS),
∵DE⊥AE,DF⊥AF,
∴∠AED=∠AFD=90°,
∴在△ADE和△ADF中,,
∴△ADE≌△ADF,
∴DE=DF.
22.如图,AD⊥BC于D,AD=BD,DC=DE,∠1与∠C有什么关系?证明你的结论.
【分析】相等,可通过证明三角形BED和ACD全等来实现,已知了一组直角和两组对应边相等因此可证得两三角形全等,也就得出了∠C=∠1的结论.
【解答】解:∠C=∠1,理由如下:
∵AD⊥BC,
∴∠ADC=∠BDE=90°.
又∵DC=DE,AD=BD,
∴△ADC≌△BDE.
∴∠C=∠1.
23.如图,∠ACB=90°,AC=BC,AD⊥CE于D,BE⊥CE于E.
(1)求证:△CBE≌△ACD;
(2)若AD=25m,DE=17m,求BE的长.
【分析】(1)先证∠CBE=∠ACD,再由AAS证明△CBE≌△ACD即可;
(2)根据全等三角形的性质得出BE=CD,CE=AD=25m,即可推出答案.
【解答】(1)证明:∵AD⊥CE于D,BE⊥CE于E,
∴∠E=∠CDA=∠ACB=90°,
∴∠BCE+∠ACD=90°,∠BCE+∠CBE=90°,
∴∠CBE=∠ACD,
在△CBE和△ACD中,
,
∴△CBE≌△ACD(AAS);
(2)解:∵△CBE≌△ACD,
∴BE=CD,AD=CE=AD=25m,
∴BE=CD=CE﹣DE=25﹣17=8(m),
即BE的长为8m.
24.如图,四边形ABCD的对角线AC、BD相交于点O,OA=OB,OC=OD.求证:
(1)AB∥CD;
(2)△ABC≌△BAD.
【分析】(1)根据等腰三角形的性质得出∠OAB=∠OBA,∠OCD=∠ODC,求出∠OAB=∠OCD,根据平行线的判定推出即可;
(2)求出AC=BD,根据SAS推出即可.
【解答】(1)证明:∵OA=OB,OC=OD,
∴∠OAB=∠OBA,∠OCD=∠ODC,
∵∠COD=∠AOB,∠OAB+∠OBA+∠AOB=180°,∠OCD+∠ODC+∠COD=180°,
∴∠OAB=∠OBA=∠OCD=∠ODC,
即∠OAB=∠OCD,
∴AB∥CD;
(2)∵OA=OB,OC=OD,
∴AC=BD,
在△ABC和△BAD中,
,
∴△ABC≌△BAD(SAS).
