2020-2021学年人教版七年级下册第六章 实数复习课件(共20张ppt)
文档属性
| 名称 | 2020-2021学年人教版七年级下册第六章 实数复习课件(共20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 936.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-24 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
实数复习
特殊:0的算术平方根是0。
一般地,如果一个正数x的平方等于
a,即
=a,那么这个正数x叫做a的
算术平方根。a的算术平方根记为
,
读作“根号a”,a叫做被开方数。
a
1.算术平方根的定义:
一般地,如果一个数的平方等于a
,那么这个数就叫做a
的平方根(或二次方根).
这就是说,如果x
2
=
a
,那么
x
就叫做
a
的平方根.a的平方根记为
2.
平方根的定义:
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。
3.平方根的性质:
一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根,也叫做a的三次方根.记作
.
其中a是被开方数,3是根指数,符号“ ”读做“三次根号”.
3
5.立方根的性质:
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
4.立方根的定义:
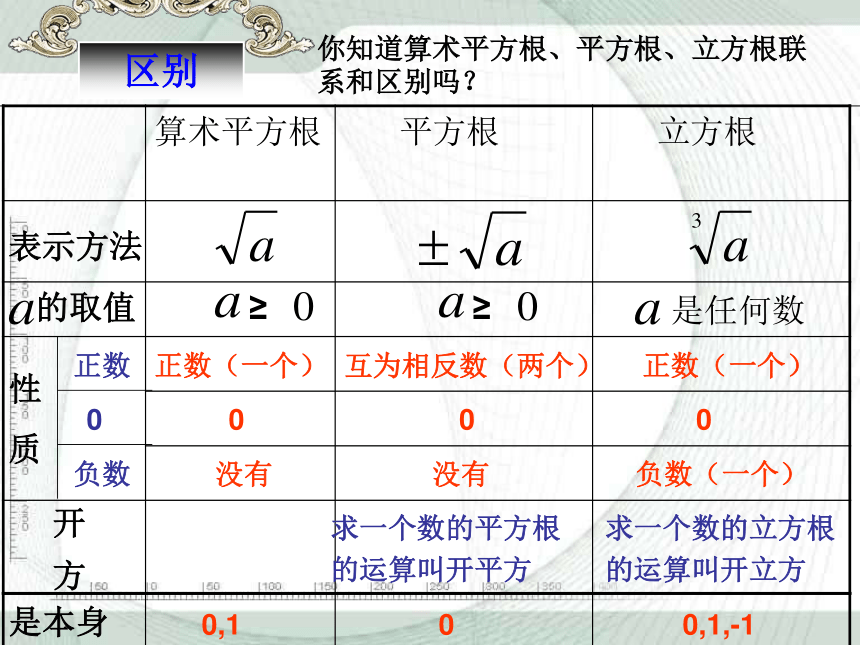
区别
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根
平方根
立方根
表示方法
的取值
性
质
≥
开
方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
是本身
0,1
0
0,1,-1
下列说法正确的是(
)
B
1、
64
±8
8
-4
2、
3、
4、
5、
6、
如果一个数的平方根为a+1和2a-7,
这个数为
。
9
7.说出下列各数的平方根:
(1)
(2)
(3)
8.x取何值时,下列各式有意义
:
(1)
(2)
(3)
(x≥-4)
(X为任意实数)
(X为任意实数)
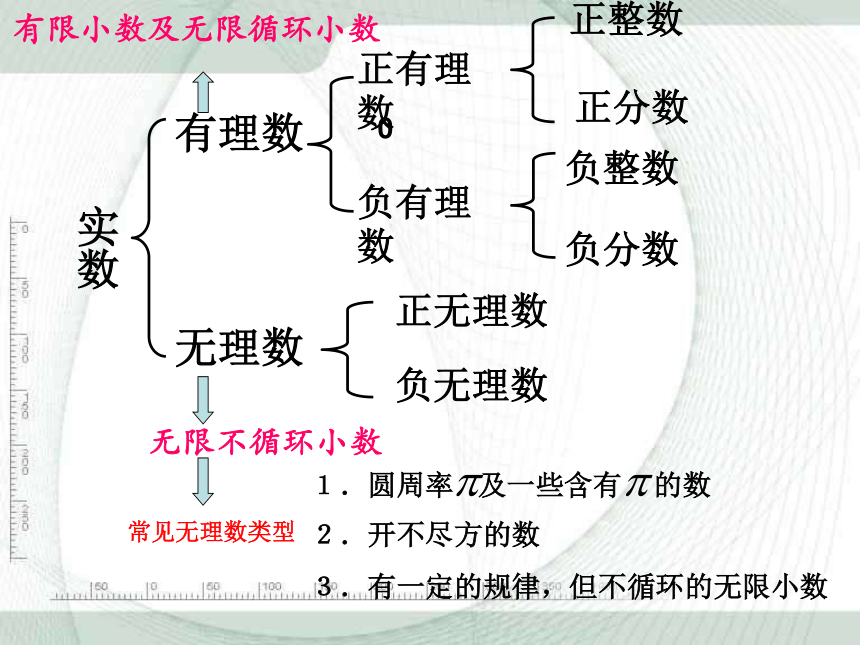
实数
有理数
无理数
正整数
正分数
负整数
负分数
负有理数
正有理数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
常见无理数类型
1.圆周率
及一些含有
的数
2.开不尽方的数
3.有一定的规律,但不循环的无限小数
0
练一练
1、判断下列说法是否正确:
⑴.实数不是有理数就是无理数。
(
)
⑵.无限小数都是无理数。
(
)
⑶.无理数都是无限小数。
(
)
⑷.带根号的数都是无理数。
(
)
⑸.两个无理数之积一定是无理数。(
)
⑹.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。(
)
2、把下列各数分别填入相应的集合内:
有理数集合
无理数集合
二、实数范围内的相关概念
1.
-
5的相反数是___;-
5的绝对值是___.
2.
5
5
实数范围内相反数和绝对值
的意义与有理数范围内相同!
3、说出下列数的相反数和绝对值:
三、相关知识的综合运用
若
,则
2.下列数中是无理数的有_________.
,
,
,
3.求下列数的绝对值和相反数.
,
4.求满足下列式子的
的值.
巩固练习
(1)
先定符号
再计算
四、实数的运算
加法结合律和交换律
在无理数计算中也成立!
(2)
四、实数的运算
1.
2.
3.
4.
练习
4.如果一个数的平方根为a+1和2a-7,
求这个数
5.已知y=
求2(x+y)的平方根
6.已知5+
的小数部分为m,
7-
的小数部分为n,求m+n的值
7.已知满足
,求a的值
练习
通过这节课的学习,你有何收获?
通过这节课的复习,你有何收获?
回顾
实数复习
特殊:0的算术平方根是0。
一般地,如果一个正数x的平方等于
a,即
=a,那么这个正数x叫做a的
算术平方根。a的算术平方根记为
,
读作“根号a”,a叫做被开方数。
a
1.算术平方根的定义:
一般地,如果一个数的平方等于a
,那么这个数就叫做a
的平方根(或二次方根).
这就是说,如果x
2
=
a
,那么
x
就叫做
a
的平方根.a的平方根记为
2.
平方根的定义:
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。
3.平方根的性质:
一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根,也叫做a的三次方根.记作
.
其中a是被开方数,3是根指数,符号“ ”读做“三次根号”.
3
5.立方根的性质:
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
4.立方根的定义:
区别
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根
平方根
立方根
表示方法
的取值
性
质
≥
开
方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
是本身
0,1
0
0,1,-1
下列说法正确的是(
)
B
1、
64
±8
8
-4
2、
3、
4、
5、
6、
如果一个数的平方根为a+1和2a-7,
这个数为
。
9
7.说出下列各数的平方根:
(1)
(2)
(3)
8.x取何值时,下列各式有意义
:
(1)
(2)
(3)
(x≥-4)
(X为任意实数)
(X为任意实数)
实数
有理数
无理数
正整数
正分数
负整数
负分数
负有理数
正有理数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
常见无理数类型
1.圆周率
及一些含有
的数
2.开不尽方的数
3.有一定的规律,但不循环的无限小数
0
练一练
1、判断下列说法是否正确:
⑴.实数不是有理数就是无理数。
(
)
⑵.无限小数都是无理数。
(
)
⑶.无理数都是无限小数。
(
)
⑷.带根号的数都是无理数。
(
)
⑸.两个无理数之积一定是无理数。(
)
⑹.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。(
)
2、把下列各数分别填入相应的集合内:
有理数集合
无理数集合
二、实数范围内的相关概念
1.
-
5的相反数是___;-
5的绝对值是___.
2.
5
5
实数范围内相反数和绝对值
的意义与有理数范围内相同!
3、说出下列数的相反数和绝对值:
三、相关知识的综合运用
若
,则
2.下列数中是无理数的有_________.
,
,
,
3.求下列数的绝对值和相反数.
,
4.求满足下列式子的
的值.
巩固练习
(1)
先定符号
再计算
四、实数的运算
加法结合律和交换律
在无理数计算中也成立!
(2)
四、实数的运算
1.
2.
3.
4.
练习
4.如果一个数的平方根为a+1和2a-7,
求这个数
5.已知y=
求2(x+y)的平方根
6.已知5+
的小数部分为m,
7-
的小数部分为n,求m+n的值
7.已知满足
,求a的值
练习
通过这节课的学习,你有何收获?
通过这节课的复习,你有何收获?
回顾
