平行四边形的判定习题课

课题: 平行四边形的判定小测
导 学 内 容 个 性 笔 记
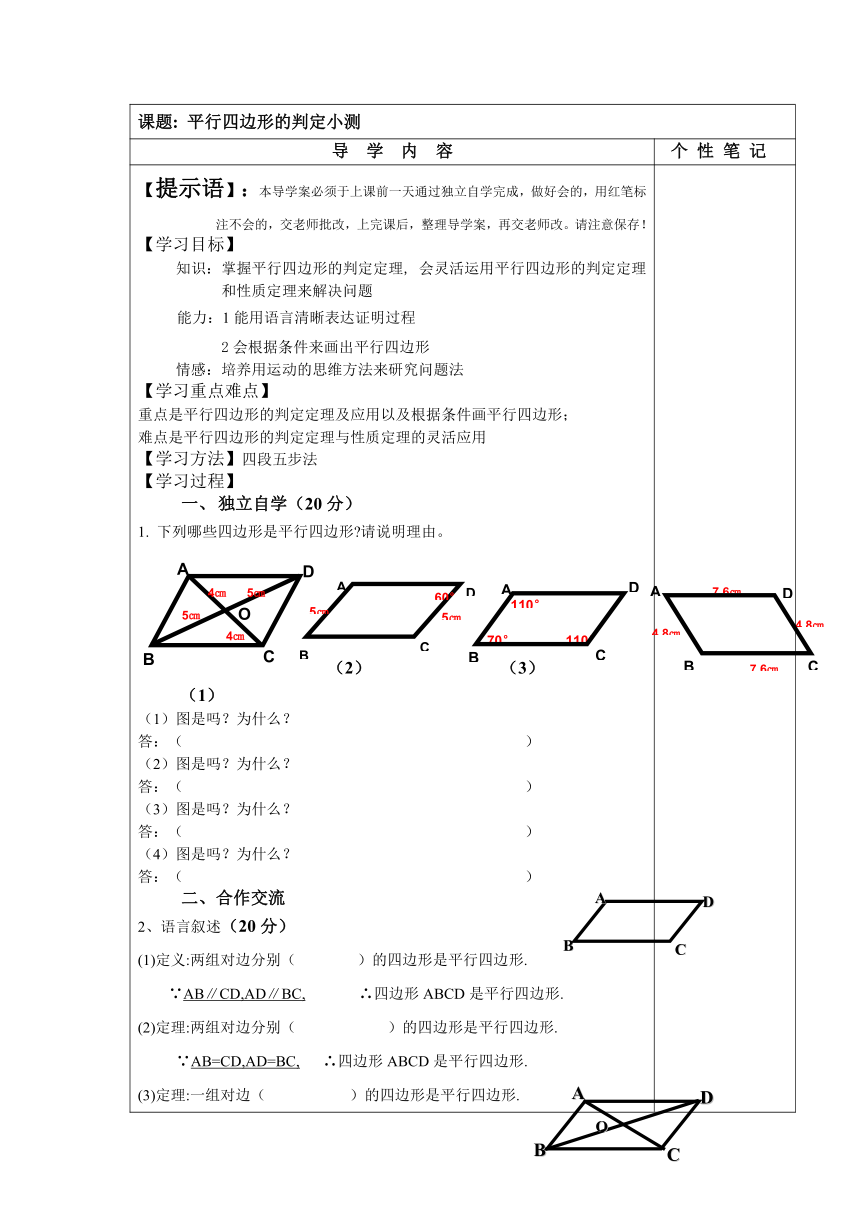
【提示语】：本导学案必须于上课前一天通过独立自学完成，做好会的，用红笔标注不会的，交老师批改，上完课后，整理导学案，再交老师改。请注意保存！【学习目标】知识：掌握平行四边形的判定定理, 会灵活运用平行四边形的判定定理和性质定理来解决问题能力：1能用语言清晰表达证明过程 2会根据条件来画出平行四边形情感：培养用运动的思维方法来研究问题法【学习重点难点】重点是平行四边形的判定定理及应用以及根据条件画平行四边形；难点是平行四边形的判定定理与性质定理的灵活应用【学习方法】四段五步法【学习过程】独立自学（20分）1. 下列哪些四边形是平行四边形 请说明理由。 （2） （3） （1） （1）图是吗？为什么？答：（ ）（2）图是吗？为什么？答：（ ）（3）图是吗？为什么？答：（ ）（4）图是吗？为什么？答：（ ）二、合作交流2、语言叙述（20分）(1)定义:两组对边分别（ ）的四边形是平行四边形.∵AB∥CD,AD∥BC, ∴四边形ABCD是平行四边形.(2)定理:两组对边分别（ ）的四边形是平行四边形.∵AB=CD,AD=BC, ∴四边形ABCD是平行四边形.(3)定理:一组对边（ ）的四边形是平行四边形.∵AB∥CD,AB=CD, ∴四边形ABCD是平行四边形.(4)定理:对角线（ ）的四边形是平行四边形.∵AO=CO,BO=DO, ∴四边形ABCD是平行四边形. (5)定理:两组对角分别（ ）的四边形是平行四边形∵∠A=∠C,∠B=∠D. ∴四边形ABCD是平行四边形.三、质疑探究（20分）3 已知： E、F是□ABCD对角线AC 上的两点，并且AE=CF。求证：四边形BFDE是平行四边形 四、检测巩固（20分）4 变式一：如图，在□ABCD中，E，F为AC上两点，BE//DF．求证：四边形BEDF为平行四边形五 拓展应用（20分）5 变式二：如图，在□ABCD中，E,F分别是AC上两点，BE⊥AC于E，DF⊥AC于F.求证:四边形BEDF为平行四边形
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
A
D
C
B
110°
70°
110°
A
B
C
D
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
D
C
A
B
D
C
A
O