初升高衔接课6-二次函数的思维模型(含答案)
文档属性
| 名称 | 初升高衔接课6-二次函数的思维模型(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-24 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初升高衔接课6-二次函数的思维模型
一、二次函数的基本性质
要点一、二次函数的基本形式
(1)一般式:(a≠0).已知图象上三点或三对、的值,通常选择一般式.
(2)顶点式:(a≠0).已知图象的顶点或对称轴,通常选择顶点式.
(3)“交点式”:已知图象与轴的交点坐标、,
要点二、二次函数的判别式
的图象
的解 方程有两个不等实数解 方程有两个相等实数解
方程没有实数解
要点三、二次函数的对称轴与对称性
(1)对称轴:,用于分开二次函数的增减性
(2)对称性:当y值相同时,x1与x2关于对称轴对称
要点四、二次函数的取值范围
注意x的取值是否含顶点
注意寻找最值
定义y的范围称函数的值域,x的范围称函数的定义域
一,二次函数的值域问题
例1.已知函数,当时,值域是 ;当时,值域是 ;当时,值域是 ;
答案:,,;
【变式1】已知函数,当时,值域是 ;当时,值域是 ;当时,值域是 ;
答案:,,;
【变式2】已知函数,当时,值域是 ;当时,值域是 ;当时,值域是 ;.
答案:,,;
【变式3】函数的值域是
答案:;
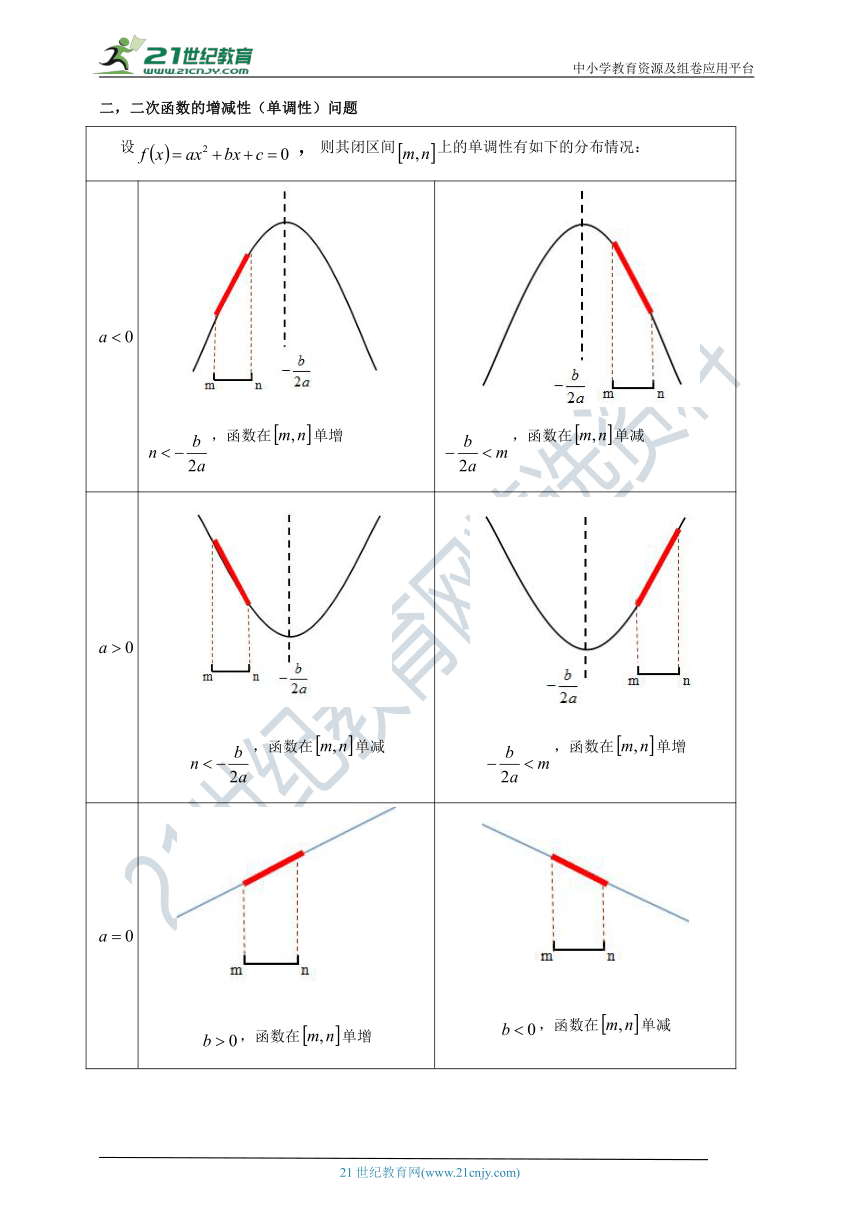
二,二次函数的增减性(单调性)问题
设,则其闭区间上的单调性有如下的分布情况:
,函数在单增
,函数在单减
,函数在单减
,函数在单增
,函数在单增
,函数在单减
例2.(1)已知二次函数,求增减性
(2)函数在[-1,2]上是单调减函数,求实数m的取值范围。
答案:;
【变式4】函数在上是增函数,则的取值范围是______.
答案:;
【变式5】函数在上是减函数,则的取值范围是__ ___.
答案:;
【变式6】如果函数在区间上是增函数,求的取值范围.
答案:;
【变式7】已知函数.求实数的取值范围,使在区间上是单调函数。
【答案】对称轴当或时,在上单调∴或。
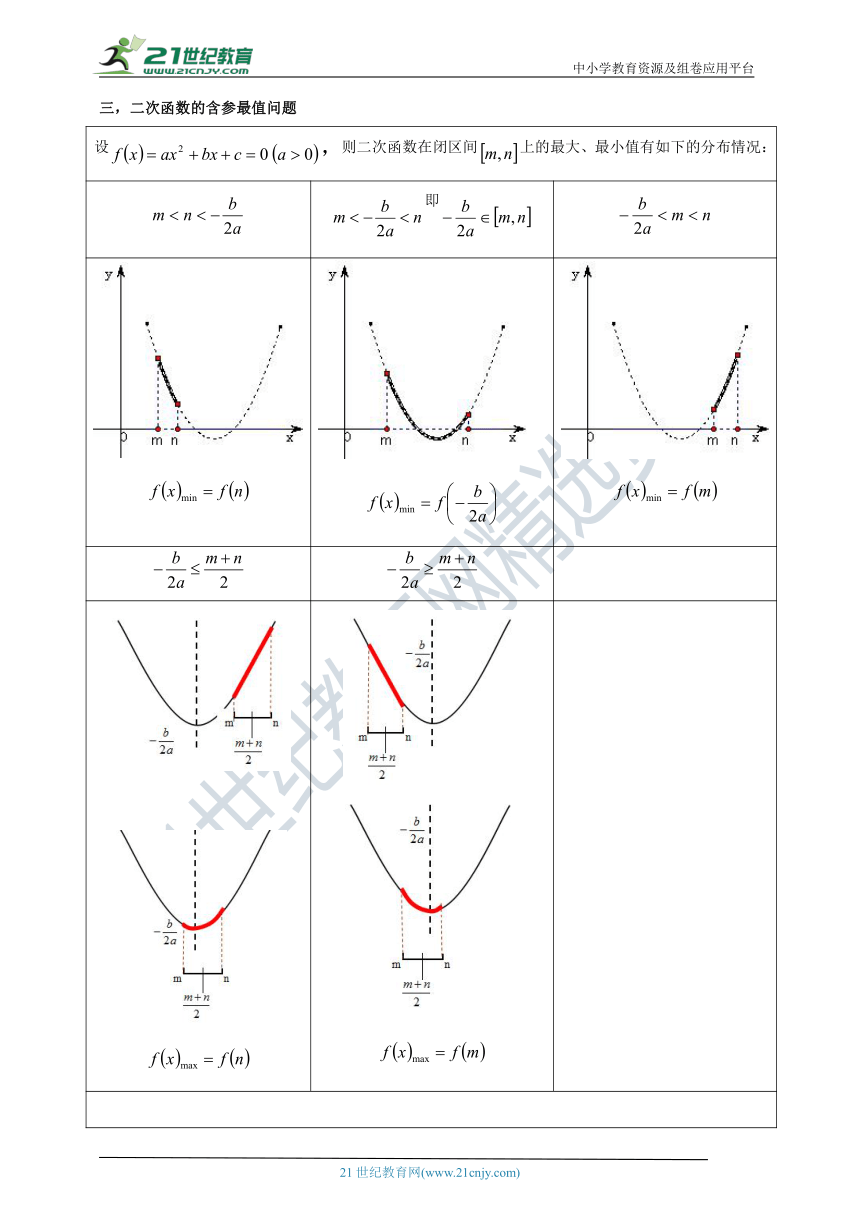
三,二次函数的含参最值问题
设,则二次函数在闭区间上的最大、最小值有如下的分布情况:
即
例3.求函数在区间上的最小值
答案:解:对称轴
(1)当即时,;
(2)当即时,;
(3)当即时,
例4.求函数的最小值?最大值?
答案:求最小值:
解:对称轴
(1)当时,;
(2)当时,;
(3)当时,
求最大值:解:(1)当时,;
(2)当时,。
【变式8】求函数在区间上的最大值。
答案:解:
【变式9】已知二次函数,当上有最小值,求的解析式。
答案:
【变式10】当时,求函数的最小值
解析:对称轴
当,即时,是的递增区间,;
当,即时,是的递减区间,;
当,即时,
例5.已知在区间内有一最大值,求的值
解析:对称轴,当即时,是的递减区间,
则,得或,而,即;
当即时,是的递增区间,则,
得或,而,即不存在;当即时,
则,即;∴或
【变式11】若a>0,当时,函数的最小值是-4,最大值是0,求a、b的值
答案:;解析:或
四,二次函数的零点分析问题
二次函数零点分析: 理解以及识记二次函数零点分析的几种类型和处理方法,其他情况最需要稍加变型即可。开口向下的情况如此雷同。
(1)两零点在两边;
令: (2)两零点在区间外;
令: (3)两零点在一边;
令:,
,; (4)一零点在中间;
令:
(5)两零点在区间内;
令:,;
,;
(6)两零点在两区间
令:
;;
,;
(7)没有零点或一个零点
没有零点,令: ;
一个零点,令: ;
没有零点或一个零点,令: ;
例6.已知(其中),当满足什么条件时会出现下面的图像:
【变式12】已知(其中),当满足什么条件时会出现下面的图像:
【变式13】设有一元二次方程x2+2(m-1)x+(m+2)=0.试问:
(1)m为何值时,有一正根、一负根.
(2)m为何值时,有一根大于1、另一根小于1.
(3)m为何值时,有两正根.
(4)m为何值时,有两负根.
(5)m为何值时,仅有一根在[1,4]内?
答案:(1)m<-2.(2);(3)(4)(5)
解:(1)设方程一正根x2,一负根x1,显然x1、x2<0,依违达定理有m+2<0.
∴ m<-2.
反思回顾:x1、x2<0条件下,ac<0,因此能保证△>0.
(2)设x1<1,x2>1,则x1-1<0,x2-1>0只要求(x1-1)(x2-1)<0,即x1x2-(x1+x2)+1<0.
依韦达定理有
(m+2)+2(m-1)+1<0.
(3)若x1>0,x2>0,则x1+x2>0且x1,x2>0,故应满足条件
依韦达定理有
(5)由图象不难知道,方程f(x)=0在[3,4]内仅有一实根条件为f(3)·f(4)<0,即
[9+6(m-1)+(m+2)]·[16+8(m-1)+(m+2)]<0.
∴(7m+1)(9m+10)<0.
【变式14】已知关于x的方程(m-1)x2-2mx+m2+m-6=0有两个实根α,β,且满足0<α<1<β,求实数m的取值范围.
解:设f(x)=x2-2mx+m2+m-6,则方程f(x)=0的两个根α,β,就是抛物线y=f(x)与x轴的两个交点的横坐标.
如图,0<α<1<β的条件是
解得
【变式15】当m为何值时,方程 有两个负数根?
解:负数根首先是实数根,∴ ,
由根与系数关系:要使方程两实数根为负数,必须且只需两根之和为负,两根之积为正.
由以上分析,有
即
∴当 时,原方程有两个负数根.
_21?????????è?????(www.21cnjy.com)_
初升高衔接课6-二次函数的思维模型
一、二次函数的基本性质
要点一、二次函数的基本形式
(1)一般式:(a≠0).已知图象上三点或三对、的值,通常选择一般式.
(2)顶点式:(a≠0).已知图象的顶点或对称轴,通常选择顶点式.
(3)“交点式”:已知图象与轴的交点坐标、,
要点二、二次函数的判别式
的图象
的解 方程有两个不等实数解 方程有两个相等实数解
方程没有实数解
要点三、二次函数的对称轴与对称性
(1)对称轴:,用于分开二次函数的增减性
(2)对称性:当y值相同时,x1与x2关于对称轴对称
要点四、二次函数的取值范围
注意x的取值是否含顶点
注意寻找最值
定义y的范围称函数的值域,x的范围称函数的定义域
一,二次函数的值域问题
例1.已知函数,当时,值域是 ;当时,值域是 ;当时,值域是 ;
答案:,,;
【变式1】已知函数,当时,值域是 ;当时,值域是 ;当时,值域是 ;
答案:,,;
【变式2】已知函数,当时,值域是 ;当时,值域是 ;当时,值域是 ;.
答案:,,;
【变式3】函数的值域是
答案:;
二,二次函数的增减性(单调性)问题
设,则其闭区间上的单调性有如下的分布情况:
,函数在单增
,函数在单减
,函数在单减
,函数在单增
,函数在单增
,函数在单减
例2.(1)已知二次函数,求增减性
(2)函数在[-1,2]上是单调减函数,求实数m的取值范围。
答案:;
【变式4】函数在上是增函数,则的取值范围是______.
答案:;
【变式5】函数在上是减函数,则的取值范围是__ ___.
答案:;
【变式6】如果函数在区间上是增函数,求的取值范围.
答案:;
【变式7】已知函数.求实数的取值范围,使在区间上是单调函数。
【答案】对称轴当或时,在上单调∴或。
三,二次函数的含参最值问题
设,则二次函数在闭区间上的最大、最小值有如下的分布情况:
即
例3.求函数在区间上的最小值
答案:解:对称轴
(1)当即时,;
(2)当即时,;
(3)当即时,
例4.求函数的最小值?最大值?
答案:求最小值:
解:对称轴
(1)当时,;
(2)当时,;
(3)当时,
求最大值:解:(1)当时,;
(2)当时,。
【变式8】求函数在区间上的最大值。
答案:解:
【变式9】已知二次函数,当上有最小值,求的解析式。
答案:
【变式10】当时,求函数的最小值
解析:对称轴
当,即时,是的递增区间,;
当,即时,是的递减区间,;
当,即时,
例5.已知在区间内有一最大值,求的值
解析:对称轴,当即时,是的递减区间,
则,得或,而,即;
当即时,是的递增区间,则,
得或,而,即不存在;当即时,
则,即;∴或
【变式11】若a>0,当时,函数的最小值是-4,最大值是0,求a、b的值
答案:;解析:或
四,二次函数的零点分析问题
二次函数零点分析: 理解以及识记二次函数零点分析的几种类型和处理方法,其他情况最需要稍加变型即可。开口向下的情况如此雷同。
(1)两零点在两边;
令: (2)两零点在区间外;
令: (3)两零点在一边;
令:,
,; (4)一零点在中间;
令:
(5)两零点在区间内;
令:,;
,;
(6)两零点在两区间
令:
;;
,;
(7)没有零点或一个零点
没有零点,令: ;
一个零点,令: ;
没有零点或一个零点,令: ;
例6.已知(其中),当满足什么条件时会出现下面的图像:
【变式12】已知(其中),当满足什么条件时会出现下面的图像:
【变式13】设有一元二次方程x2+2(m-1)x+(m+2)=0.试问:
(1)m为何值时,有一正根、一负根.
(2)m为何值时,有一根大于1、另一根小于1.
(3)m为何值时,有两正根.
(4)m为何值时,有两负根.
(5)m为何值时,仅有一根在[1,4]内?
答案:(1)m<-2.(2);(3)(4)(5)
解:(1)设方程一正根x2,一负根x1,显然x1、x2<0,依违达定理有m+2<0.
∴ m<-2.
反思回顾:x1、x2<0条件下,ac<0,因此能保证△>0.
(2)设x1<1,x2>1,则x1-1<0,x2-1>0只要求(x1-1)(x2-1)<0,即x1x2-(x1+x2)+1<0.
依韦达定理有
(m+2)+2(m-1)+1<0.
(3)若x1>0,x2>0,则x1+x2>0且x1,x2>0,故应满足条件
依韦达定理有
(5)由图象不难知道,方程f(x)=0在[3,4]内仅有一实根条件为f(3)·f(4)<0,即
[9+6(m-1)+(m+2)]·[16+8(m-1)+(m+2)]<0.
∴(7m+1)(9m+10)<0.
【变式14】已知关于x的方程(m-1)x2-2mx+m2+m-6=0有两个实根α,β,且满足0<α<1<β,求实数m的取值范围.
解:设f(x)=x2-2mx+m2+m-6,则方程f(x)=0的两个根α,β,就是抛物线y=f(x)与x轴的两个交点的横坐标.
如图,0<α<1<β的条件是
解得
【变式15】当m为何值时,方程 有两个负数根?
解:负数根首先是实数根,∴ ,
由根与系数关系:要使方程两实数根为负数,必须且只需两根之和为负,两根之积为正.
由以上分析,有
即
∴当 时,原方程有两个负数根.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
