9.1.2 不等式的性质 课件(共26张PPT)
文档属性
| 名称 | 9.1.2 不等式的性质 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 06:50:32 | ||
图片预览




文档简介
9.1.2 不等式的性质
第九章 不等式与不等式组
2021年春人教版七年级(下)数学
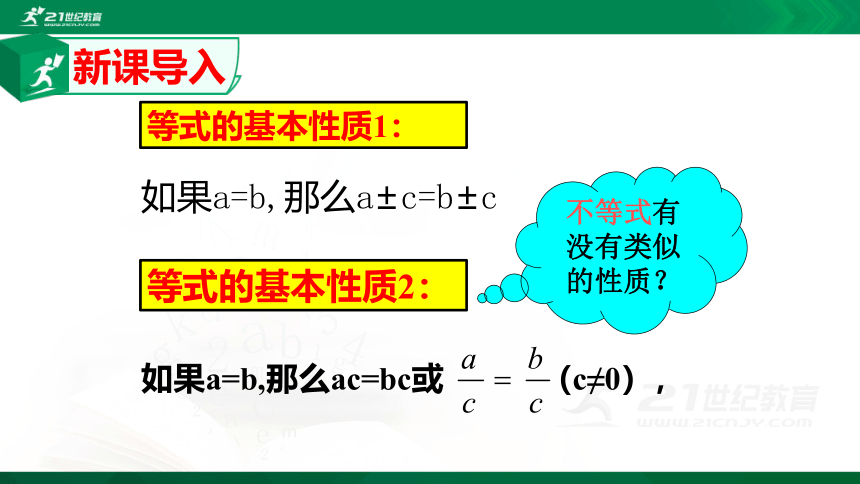
等式的基本性质1:
等式的基本性质2:
如果a=b,那么a±c=b±c
如果a=b,那么ac=bc或 (c≠0),
不等式有没有类似的性质?
新课导入
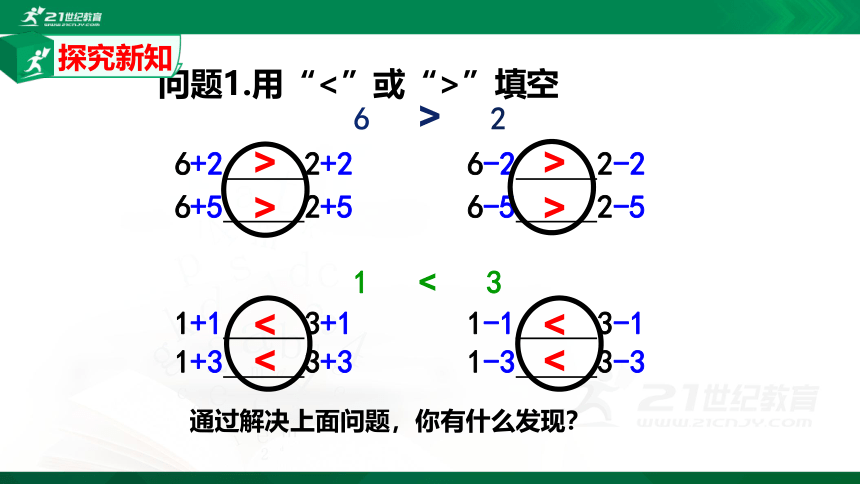
问题1.用“<”或“>”填空
6 > 2
6+2 2+2 6-2 2-2
6+5 2+5 6-5 2-5
1 < 3
1+1 3+1 1-1 3-1
1+3 3+3 1-3 3-3
>
>
>
>
<
<
<
<
通过解决上面问题,你有什么发现?
探究新知
观察不等号的变化,发现并归纳其中的规律,获得以下结论.
性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的性质1用符号语言表示
探究新知
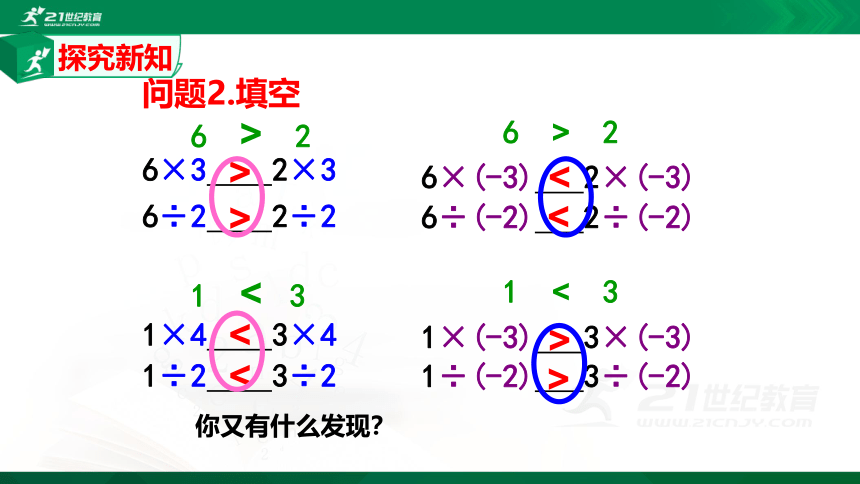
6 > 2
6×(-3) 2×(-3)
6÷(-2) 2÷(-2)
1 < 3
1×(-3) 3×(-3)
1÷(-2) 3÷(-2)
问题2.填空
6 > 2
6×3 2×3
6÷2 2÷2
1 < 3
1×4 3×4
1÷2 3÷2
>
>
>
<
<
<
<
>
你又有什么发现?
探究新知
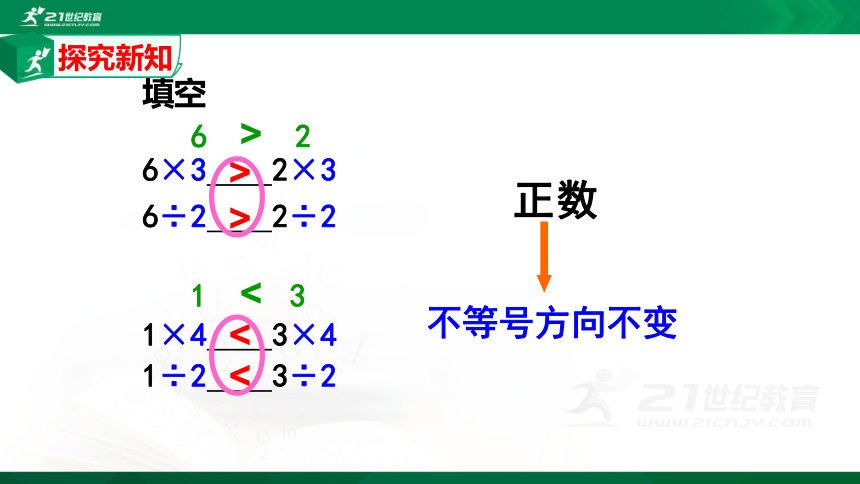
填空
6 > 2
6×3 2×3
6÷2 2÷2
1 < 3
1×4 3×4
1÷2 3÷2
>
>
<
<
不等号方向不变
正数
探究新知
用字母表示:
不等式两边 ,
不等号的方向 .
不变
乘以(或除以)同一个正数
探究新知
6 > 2
6×(-3) 2×(-3)
6÷(-2) 2÷(-2)
1 < 3
1×(-3) 3×(-3)
1÷(-2) 3÷(-2)
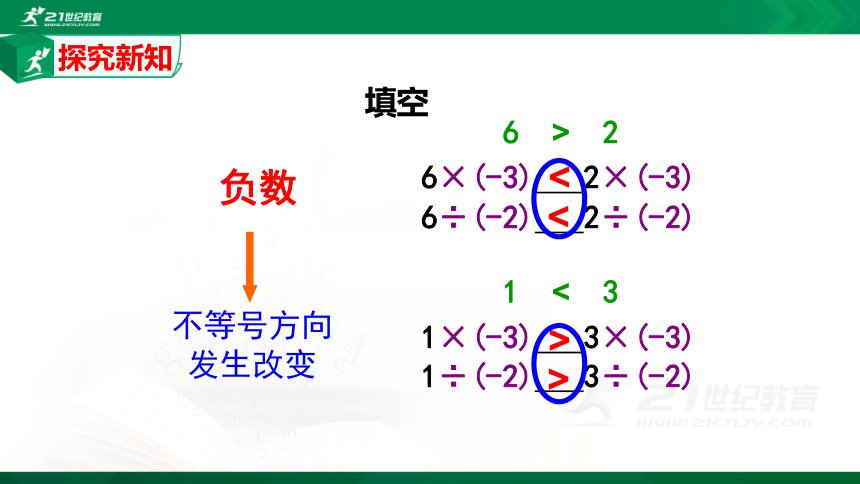
填空
>
<
<
>
不等号方向
发生改变
负数
探究新知
用字母表示:
不等式两边 ,
不等号的方向 .
发生改变
乘以(或除以)同一个负数
探究新知
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变;
不等式的性质2
如果a>b,c>0 ,那么ac>bc,
如果a>b,c<0 ,那么ac不等式的性质3
探究新知
例1 利用不等式的性质解下列不等式:
(1) x-7>26; (2) 3x<2x+1;
(3) >50; (4) -4x>3.
解未知数为x的不等式
化为x>a或x﹤a的形式
目标
方法:不等式基本性质1~3
思路:
利用不等式的性质解简单的不等式
例题讲解
解 (1)为了使不等式x-7>26中不等号的一边变为x, 根据不等式的性质1,不等式两边都加7,不等号的方向不变,得 x-7+7﹥26+7,即x﹥33.
这个不等式的解集在数轴上的表示如图所示:
0
33
例题讲解
(2)为了使不等式3x<2x+1中不等号的一边变为x,根据_____________,不等式两边都减去____,不等
号的方向_____,得 .
3x-2x﹤2x+1-2x ,即 x﹤1
这个不等式的解集在数轴上的表示如图所示:
0
1
不等式性质1
2x
不变
例题讲解
(3)为了使不等式 ﹥50中不等号的一边变为x,根据不等式的性质2,不等式的两边都除以 不等号的
方向不变,得
x﹥75.
这个不等式的解集在数轴上的表示如图所示:
0
75
例题讲解
(4)为了使不等式-4x﹥3中的不等号的一边变为x,
根据______________ ,不等式两边都除以____,
不等号的方向______,得
x﹤- .
这个不等式的解集在数轴上的表示如图所示:
-
4
3
0
不等式的性质3
-4
改变
例题讲解
解:新注入水的体积V与原有水的体积的和不能超过
容器的容积,即
V+3×5×3≤3×5×10
解得 V≤105
又由于新注入水的体积不能是负数,因此,V的取值范围是V≥0并且V≤105.
在数轴上表示V的取值范围如图
在表示0和105的点上画实心圆点,表示取值范围包括这两个数
0
105
例2. 某长方体形状的容器长5cm,宽3cm,高10cm,容器内原有水的高度为3cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出V的取值范围.
例题讲解
1 . 用“>”或“<”填空:
(1)a+3_____b+3;(ab);
(3) (a>b);
(4)a-4_____b-4 (a-b>0) ;
(5)若a>0,b>0,则ab_____0;
(6)若b<0,则a+b______a;
(7)当a<0时,b_____0时,ab>0.
<
<
<
<
>
>
>
课堂练习
(1)如果x+5>4,那么两边都 可得 x >-1
(2)在-7<8 的两边都加上9可得 。
(3)在5>-2 的两边都减去6可得 。
(4)在-3>-4 的两边都乘以7可得 。
(5)在-8<0 的两边都除以8 可得 。
减去5
2<17
-1>-8
-21 >- 28
-1<0
2.不等式的性质的应用
(6)在不等式-8<0的两边都除以-8可得 。
(7)在不等式-3 x<3的两边都除以-3可得 。
(8)在不等式-3>-4的两边都乘以-3可得 。
(9)在不等式 的两边都乘以-1可得 。
1>0
9<12
>
>
>
<
3.如果 ,那么:
①
②
③
④
(不等式性质 )
(不等式性质 )
(不等式性质 )
(不等式性质 )
1
2
2
1
4.填空
⑴若m-2>3,则m>5,依据_________ .
不等式的两边 .
⑵若-2x>4,则x<-2,依据____________.
不等式的两边 .
不等式的性质1
同时加2,不等号不变
不等式的性质3
同时除以-2,不等号方向改变
(1) 3a____3b ; (2) a-8____b-8 ;
(3) -2a____-2b ; (4) ____ ;
(5) -3.5b+1___ -3.5a+1 .
>
<
>
>
>
5. 设a>b,用“<”或“>”填空,并说明依据不等式的那条性质.
6.设 ,用“<”或“>”填空.
①
②
③
>
>
<
不等式的基本性质
不等式基本性质2
不等式基本性质3
→
→
如果
那么
如果 那么
应用
不等式的基本性质1
如果a>b,那么a+c>b+c,a-c>b-c
→
课堂小结
谢谢聆听
第九章 不等式与不等式组
2021年春人教版七年级(下)数学
等式的基本性质1:
等式的基本性质2:
如果a=b,那么a±c=b±c
如果a=b,那么ac=bc或 (c≠0),
不等式有没有类似的性质?
新课导入
问题1.用“<”或“>”填空
6 > 2
6+2 2+2 6-2 2-2
6+5 2+5 6-5 2-5
1 < 3
1+1 3+1 1-1 3-1
1+3 3+3 1-3 3-3
>
>
>
>
<
<
<
<
通过解决上面问题,你有什么发现?
探究新知
观察不等号的变化,发现并归纳其中的规律,获得以下结论.
性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的性质1用符号语言表示
探究新知
6 > 2
6×(-3) 2×(-3)
6÷(-2) 2÷(-2)
1 < 3
1×(-3) 3×(-3)
1÷(-2) 3÷(-2)
问题2.填空
6 > 2
6×3 2×3
6÷2 2÷2
1 < 3
1×4 3×4
1÷2 3÷2
>
>
>
<
<
<
<
>
你又有什么发现?
探究新知
填空
6 > 2
6×3 2×3
6÷2 2÷2
1 < 3
1×4 3×4
1÷2 3÷2
>
>
<
<
不等号方向不变
正数
探究新知
用字母表示:
不等式两边 ,
不等号的方向 .
不变
乘以(或除以)同一个正数
探究新知
6 > 2
6×(-3) 2×(-3)
6÷(-2) 2÷(-2)
1 < 3
1×(-3) 3×(-3)
1÷(-2) 3÷(-2)
填空
>
<
<
>
不等号方向
发生改变
负数
探究新知
用字母表示:
不等式两边 ,
不等号的方向 .
发生改变
乘以(或除以)同一个负数
探究新知
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变;
不等式的性质2
如果a>b,c>0 ,那么ac>bc,
如果a>b,c<0 ,那么ac
探究新知
例1 利用不等式的性质解下列不等式:
(1) x-7>26; (2) 3x<2x+1;
(3) >50; (4) -4x>3.
解未知数为x的不等式
化为x>a或x﹤a的形式
目标
方法:不等式基本性质1~3
思路:
利用不等式的性质解简单的不等式
例题讲解
解 (1)为了使不等式x-7>26中不等号的一边变为x, 根据不等式的性质1,不等式两边都加7,不等号的方向不变,得 x-7+7﹥26+7,即x﹥33.
这个不等式的解集在数轴上的表示如图所示:
0
33
例题讲解
(2)为了使不等式3x<2x+1中不等号的一边变为x,根据_____________,不等式两边都减去____,不等
号的方向_____,得 .
3x-2x﹤2x+1-2x ,即 x﹤1
这个不等式的解集在数轴上的表示如图所示:
0
1
不等式性质1
2x
不变
例题讲解
(3)为了使不等式 ﹥50中不等号的一边变为x,根据不等式的性质2,不等式的两边都除以 不等号的
方向不变,得
x﹥75.
这个不等式的解集在数轴上的表示如图所示:
0
75
例题讲解
(4)为了使不等式-4x﹥3中的不等号的一边变为x,
根据______________ ,不等式两边都除以____,
不等号的方向______,得
x﹤- .
这个不等式的解集在数轴上的表示如图所示:
-
4
3
0
不等式的性质3
-4
改变
例题讲解
解:新注入水的体积V与原有水的体积的和不能超过
容器的容积,即
V+3×5×3≤3×5×10
解得 V≤105
又由于新注入水的体积不能是负数,因此,V的取值范围是V≥0并且V≤105.
在数轴上表示V的取值范围如图
在表示0和105的点上画实心圆点,表示取值范围包括这两个数
0
105
例2. 某长方体形状的容器长5cm,宽3cm,高10cm,容器内原有水的高度为3cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出V的取值范围.
例题讲解
1 . 用“>”或“<”填空:
(1)a+3_____b+3;(a
(3) (a>b);
(4)a-4_____b-4 (a-b>0) ;
(5)若a>0,b>0,则ab_____0;
(6)若b<0,则a+b______a;
(7)当a<0时,b_____0时,ab>0.
<
<
<
<
>
>
>
课堂练习
(1)如果x+5>4,那么两边都 可得 x >-1
(2)在-7<8 的两边都加上9可得 。
(3)在5>-2 的两边都减去6可得 。
(4)在-3>-4 的两边都乘以7可得 。
(5)在-8<0 的两边都除以8 可得 。
减去5
2<17
-1>-8
-21 >- 28
-1<0
2.不等式的性质的应用
(6)在不等式-8<0的两边都除以-8可得 。
(7)在不等式-3 x<3的两边都除以-3可得 。
(8)在不等式-3>-4的两边都乘以-3可得 。
(9)在不等式 的两边都乘以-1可得 。
1>0
9<12
>
>
>
<
3.如果 ,那么:
①
②
③
④
(不等式性质 )
(不等式性质 )
(不等式性质 )
(不等式性质 )
1
2
2
1
4.填空
⑴若m-2>3,则m>5,依据_________ .
不等式的两边 .
⑵若-2x>4,则x<-2,依据____________.
不等式的两边 .
不等式的性质1
同时加2,不等号不变
不等式的性质3
同时除以-2,不等号方向改变
(1) 3a____3b ; (2) a-8____b-8 ;
(3) -2a____-2b ; (4) ____ ;
(5) -3.5b+1___ -3.5a+1 .
>
<
>
>
>
5. 设a>b,用“<”或“>”填空,并说明依据不等式的那条性质.
6.设 ,用“<”或“>”填空.
①
②
③
>
>
<
不等式的基本性质
不等式基本性质2
不等式基本性质3
→
→
如果
那么
如果 那么
应用
不等式的基本性质1
如果a>b,那么a+c>b+c,a-c>b-c
→
课堂小结
谢谢聆听
