2020-2021学年人教版八年级下册数学 18.2.3正方形 同步习题 (Word版 含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学 18.2.3正方形 同步习题 (Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 97.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 11:43:15 | ||
图片预览

文档简介
18.2.3正方形 同步习题
一.选择题
1.下列说法正确的是 )
A.有一个角是直角的平行四边形是正方形
B.对角线互相垂直的矩形是正方形
C.有一组邻边相等的菱形是正方形
D.各边都相等的四边形是正方形
2.如图,正方形ABCD,点E、F分别在BC、CD上,AE=BF,下列结论错误的是( )
A.BE=CF B.∠AEB+∠BFC=180°
C.∠DAE=∠BFC D.AE⊥BF
3.将三个大小不同的正方形如图放置,顶点处两两相接,若正方形A的边长为4,正方形C的边长为3,则正方形B的面积为( )
A.25 B.5 C.16 D.12
4.有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2等于( )
A.4:9 B.2:3 C.1:2 D.1:
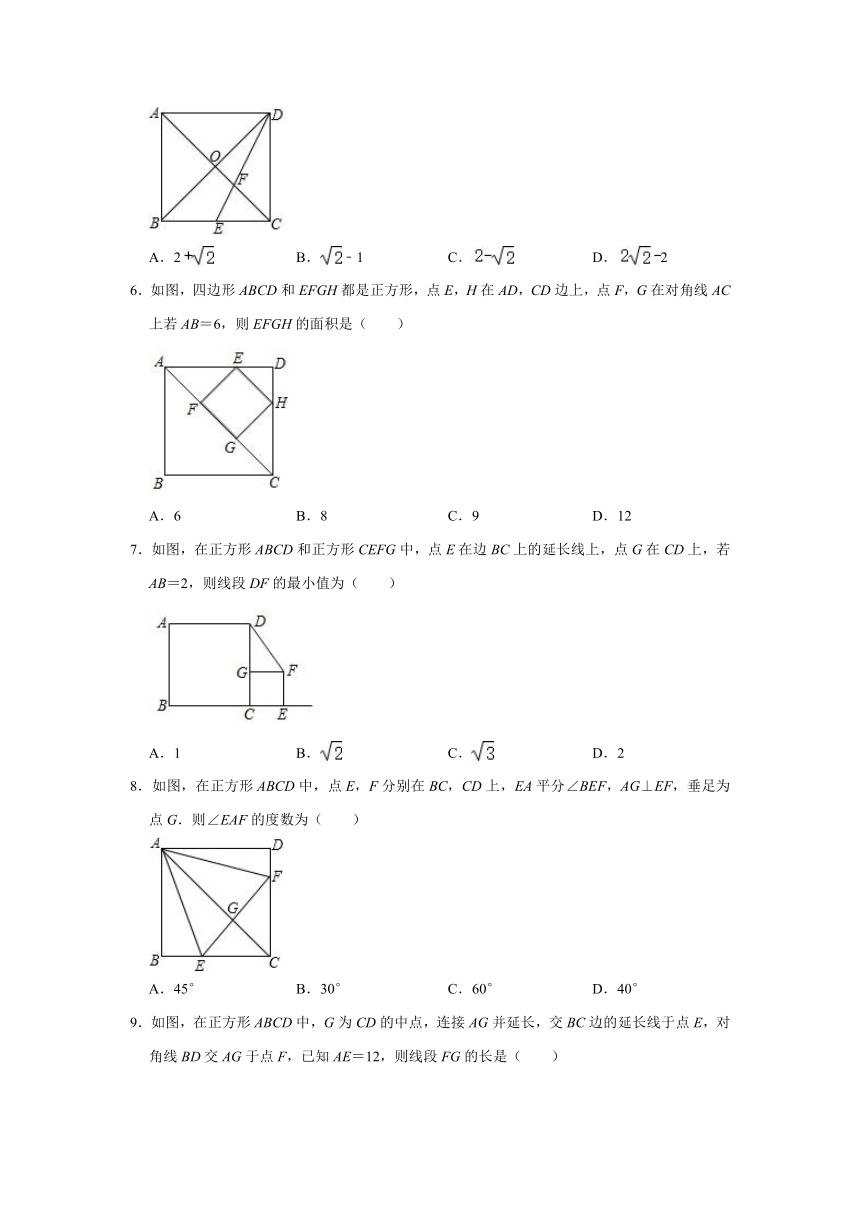
5.如图,正方形ABCD中,AC与BD相交于点O,DE平分∠BDC交AC于F,交BC于E.若正方形ABCD的边长为2,则OF的值为( )
A.2 B.﹣1 C. D.2
6.如图,四边形ABCD和EFGH都是正方形,点E,H在AD,CD边上,点F,G在对角线AC上若AB=6,则EFGH的面积是( )
A.6 B.8 C.9 D.12
7.如图,在正方形ABCD和正方形CEFG中,点E在边BC上的延长线上,点G在CD上,若AB=2,则线段DF的最小值为( )
A.1 B. C. D.2
8.如图,在正方形ABCD中,点E,F分别在BC,CD上,EA平分∠BEF,AG⊥EF,垂足为点G.则∠EAF的度数为( )
A.45° B.30° C.60° D.40°
9.如图,在正方形ABCD中,G为CD的中点,连接AG并延长,交BC边的延长线于点E,对角线BD交AG于点F,已知AE=12,则线段FG的长是( )
A.2 B.4 C.5 D.6
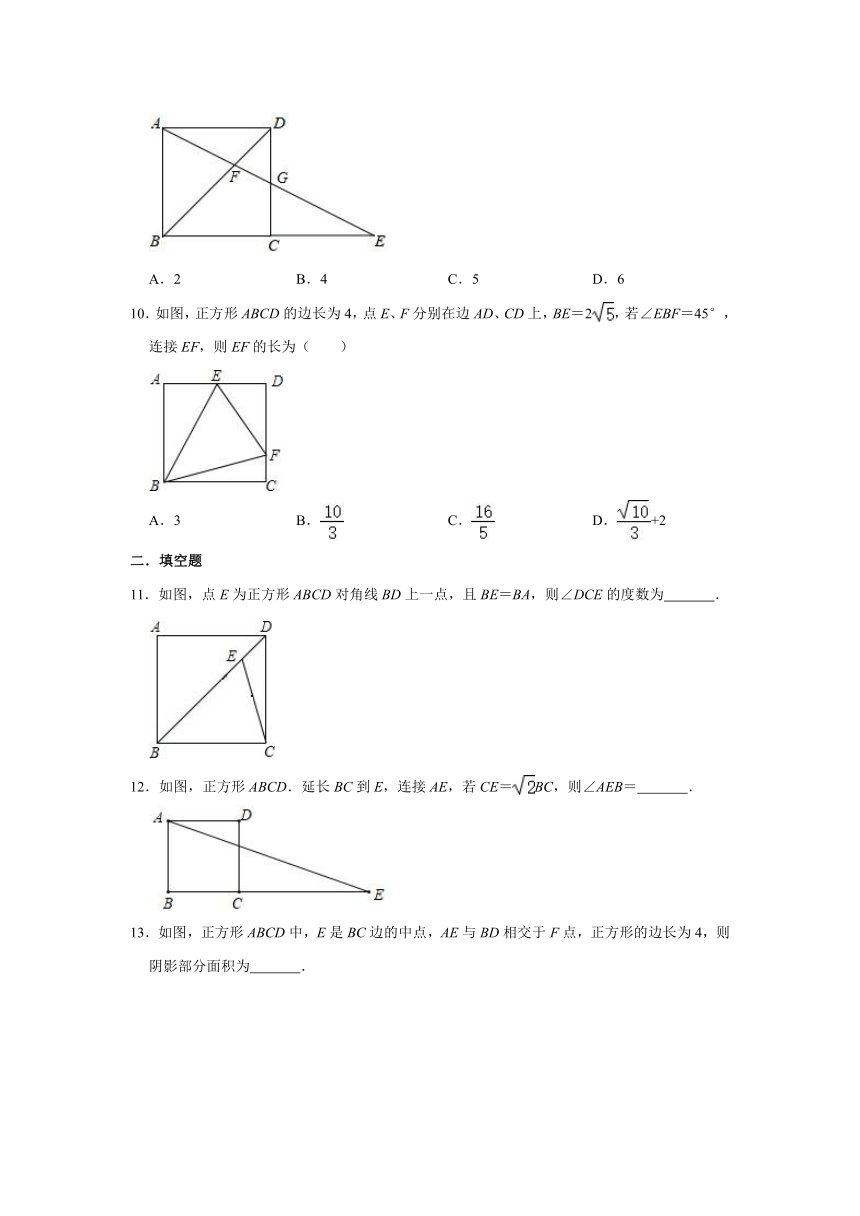
10.如图,正方形ABCD的边长为4,点E、F分别在边AD、CD上,BE=2,若∠EBF=45°,连接EF,则EF的长为( )
A.3 B. C. D.+2
二.填空题
11.如图,点E为正方形ABCD对角线BD上一点,且BE=BA,则∠DCE的度数为 .
12.如图,正方形ABCD.延长BC到E,连接AE,若CE=BC,则∠AEB= .
13.如图,正方形ABCD中,E是BC边的中点,AE与BD相交于F点,正方形的边长为4,则阴影部分面积为 .
14.如图,四边形ABCD是正方形,P在CD上,已知△ADP≌△ABP′,AB=6,DP=2,求PP′= .
15.如图,正方形ABCD的面积为5,正方形CEFG的面积为2,点G在线段CD上,且B、C、E三点在一条直线上,联结AC、AE,则△ACE的面积是 .
三.解答题
16.如图,在正方形ABCD中,点E是BC上的一点,点F是CD延长线上的一点,且BE=DF,连接AE、AF、EF.求证:△ABE≌△ADF.
17.如图,已知正方形ABCD的边长为6,点E在CD边上,以线段CE为边长在正方形ABCD的外部作正方形CEFG,以线段AD和DE为邻边作矩形ADEH,若S正方形CEFG=S矩形ADEH.
(1)求线段CE的长;
(2)若点M为BC边的中点,连接MD,求证:MD=MG.
18.如图,在正方形ABCD的外侧,作等边三角形ADE,线段BE与AC交于点F.
(1)求∠AEB和∠BFC的度数;
(2)若AD=6,求BE2的值.
参考答案
1.B
2.B
3.A
4.A
5.C
6.B
7.B
8.A
9.A
10.B
11.22.5°
12.22.5°
13.
14.4
15.
16.证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠ADC=90°,
∴∠ADF=90°,
∴∠B=∠ADF,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS).
17.(1)3﹣3;
(2)证明:∵点M为BC边的中点,
∴MC=3,
在Rt△MCD中,DM==3,
∵MG=MC+CG=3+3﹣3=3,
∴MD=MG.
18.解:(1)∵四边形ABCD是正方形,
∴AB=AD,
又∵△ADE是等边三角形,
∴AE=AD=DE,∠DAE=60°,
∴AB=AE,
∴∠ABE=∠AEB,∠BAE=90°+60°=150°,
∴∠ABE=(180°﹣150°)÷2=15°,
又∵∠BAC=45°,
∴∠BFC=45°+15°=60°.
(2)过E作EG⊥AD,并与AB交于H,
∵△ADE是等边三角形,EG⊥AD,
∴AG=GD=3,
∴GE=3,
∵四边形ABCD是正方形,
∴BH=3,
∵HE=HG+GE=6+3,
在Rt△BHE中,BE2=.
一.选择题
1.下列说法正确的是 )
A.有一个角是直角的平行四边形是正方形
B.对角线互相垂直的矩形是正方形
C.有一组邻边相等的菱形是正方形
D.各边都相等的四边形是正方形
2.如图,正方形ABCD,点E、F分别在BC、CD上,AE=BF,下列结论错误的是( )
A.BE=CF B.∠AEB+∠BFC=180°
C.∠DAE=∠BFC D.AE⊥BF
3.将三个大小不同的正方形如图放置,顶点处两两相接,若正方形A的边长为4,正方形C的边长为3,则正方形B的面积为( )
A.25 B.5 C.16 D.12
4.有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2等于( )
A.4:9 B.2:3 C.1:2 D.1:
5.如图,正方形ABCD中,AC与BD相交于点O,DE平分∠BDC交AC于F,交BC于E.若正方形ABCD的边长为2,则OF的值为( )
A.2 B.﹣1 C. D.2
6.如图,四边形ABCD和EFGH都是正方形,点E,H在AD,CD边上,点F,G在对角线AC上若AB=6,则EFGH的面积是( )
A.6 B.8 C.9 D.12
7.如图,在正方形ABCD和正方形CEFG中,点E在边BC上的延长线上,点G在CD上,若AB=2,则线段DF的最小值为( )
A.1 B. C. D.2
8.如图,在正方形ABCD中,点E,F分别在BC,CD上,EA平分∠BEF,AG⊥EF,垂足为点G.则∠EAF的度数为( )
A.45° B.30° C.60° D.40°
9.如图,在正方形ABCD中,G为CD的中点,连接AG并延长,交BC边的延长线于点E,对角线BD交AG于点F,已知AE=12,则线段FG的长是( )
A.2 B.4 C.5 D.6
10.如图,正方形ABCD的边长为4,点E、F分别在边AD、CD上,BE=2,若∠EBF=45°,连接EF,则EF的长为( )
A.3 B. C. D.+2
二.填空题
11.如图,点E为正方形ABCD对角线BD上一点,且BE=BA,则∠DCE的度数为 .
12.如图,正方形ABCD.延长BC到E,连接AE,若CE=BC,则∠AEB= .
13.如图,正方形ABCD中,E是BC边的中点,AE与BD相交于F点,正方形的边长为4,则阴影部分面积为 .
14.如图,四边形ABCD是正方形,P在CD上,已知△ADP≌△ABP′,AB=6,DP=2,求PP′= .
15.如图,正方形ABCD的面积为5,正方形CEFG的面积为2,点G在线段CD上,且B、C、E三点在一条直线上,联结AC、AE,则△ACE的面积是 .
三.解答题
16.如图,在正方形ABCD中,点E是BC上的一点,点F是CD延长线上的一点,且BE=DF,连接AE、AF、EF.求证:△ABE≌△ADF.
17.如图,已知正方形ABCD的边长为6,点E在CD边上,以线段CE为边长在正方形ABCD的外部作正方形CEFG,以线段AD和DE为邻边作矩形ADEH,若S正方形CEFG=S矩形ADEH.
(1)求线段CE的长;
(2)若点M为BC边的中点,连接MD,求证:MD=MG.
18.如图,在正方形ABCD的外侧,作等边三角形ADE,线段BE与AC交于点F.
(1)求∠AEB和∠BFC的度数;
(2)若AD=6,求BE2的值.
参考答案
1.B
2.B
3.A
4.A
5.C
6.B
7.B
8.A
9.A
10.B
11.22.5°
12.22.5°
13.
14.4
15.
16.证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠ADC=90°,
∴∠ADF=90°,
∴∠B=∠ADF,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS).
17.(1)3﹣3;
(2)证明:∵点M为BC边的中点,
∴MC=3,
在Rt△MCD中,DM==3,
∵MG=MC+CG=3+3﹣3=3,
∴MD=MG.
18.解:(1)∵四边形ABCD是正方形,
∴AB=AD,
又∵△ADE是等边三角形,
∴AE=AD=DE,∠DAE=60°,
∴AB=AE,
∴∠ABE=∠AEB,∠BAE=90°+60°=150°,
∴∠ABE=(180°﹣150°)÷2=15°,
又∵∠BAC=45°,
∴∠BFC=45°+15°=60°.
(2)过E作EG⊥AD,并与AB交于H,
∵△ADE是等边三角形,EG⊥AD,
∴AG=GD=3,
∴GE=3,
∵四边形ABCD是正方形,
∴BH=3,
∵HE=HG+GE=6+3,
在Rt△BHE中,BE2=.
