8.3简单几何体的表面积与体积-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(17张PPT)
文档属性
| 名称 | 8.3简单几何体的表面积与体积-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 489.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-24 19:56:42 | ||
图片预览





文档简介
第八章立体图形初步
8.3简单几何体的表面积与体积
了解棱柱、棱锥、棱台的表面积与体积的计算公式
01
理解并掌握侧面展开图与几何体的表面积之间的关系
02
能用计算公式求几何体的表面积与体积
03
学习目标
棱柱、棱锥、棱台的表面积
01
02
03
01
棱柱、棱锥、棱台的表面积
多面体的表面积就是围成多面体各个面的面积的和,棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和
棱柱、棱锥、棱台的体积
02
02
03
02
棱柱:柱体的底面面积为S,高为h,则V=Sh
棱锥:椎体的底面面积为S,高为h,则V= Sh
棱台:台体的上、下底面面积分别为 , ,高为h,则
圆柱、圆锥、圆台的表面积
02
02
03
03
表面积
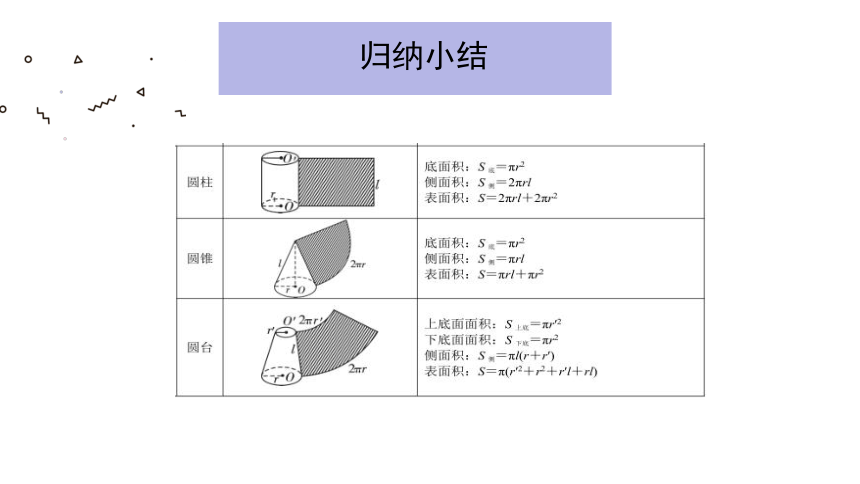
1.圆柱表面积: (r是底面半径,l是母线长)
2.圆锥表面积: = (r是底面半径,l是母线长)
3.圆台表面积: ( 分别是上、下底面半径, 是母线长)
归纳小结
01
02
03
01
圆柱、圆锥、圆台体积
02
02
03
04
体积
(1)圆柱体积: (r是底面半径,h是高)
(2)圆锥体积: (r是底面半径,h是高)
(3)圆台体积: ( 分别是上、下底面半径,是高)
名师点拨
01
02
03
01
柱体、椎体的体积公式可以看做台体体积公式的“特殊形式”
球的表面积和体积
02
02
03
05
球的表面积:
球的体积:
几个与球有关的切、接的常用理论
02
02
03
06
(1)正方体的棱长为a,球的半径为R
①若球为正方体的外接球,则2R=3a
②若球为正方体的内接球,则2R=a
③若球与正方体的各棱相切,则2R=2a
(2)若长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R=
?
例1
经典例题
围屋始建于唐宋,兴盛于明清.围屋结合了中原古朴遗风以及南方文化的地域特色,是中国五大民居特色建筑之一在形式上主要有方形围屋、半圆形围屋、圆形围屋,如图所示是墙体厚度为1m的圆形围屋(主要用泥土建筑而成,大部分是客家民居,又称客家土围楼),从地面测量内环直径是16m,外环直径是30m,墙体高10m,则该围屋所有房间的室内总体积(斜屋顶不计入室内体积及忽略房间之间的墙体厚度与楼板厚度)大约是( )
A. B. C. D.
解析
经典例题
【详解】
因为墙体厚度为1m,所以除去墙体厚度的外环直径变为(30-2)m,加上墙体厚度的内环直径变为(16+2)m,墙体高10m,由题意得围屋所有房间的室内总体积为 .
故选:D.
例2
经典例题
《九章算术》是我国古代数学名著﹐它在几何学中的研究比西方早1000多年.在《九章算术》中,将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马.如图 是阳马, 平面 , .则该阳马的外接球的表面积为( )
A. B. C. D.
解析
经典例题
【详解】
连接AC,BD,交于 ,取PC中点O,连接 ,如图所示
因为 分别为PC,AC的中点,所以 ,
又 平面ABCD,所以 平面ABCD,
所以O到A,B,C,D的距离都相等,又 ,
所以O为该四棱锥的外接球的球心,
在 中, , ,
所以 ,
所以该四棱锥的外接球的半径 ,
所以该阳马的外接球的表面积 .
故选:B
随堂练习
我国古代数学名著《九章算术》卷五“商功”中有这样一题:今有堤下广二丈,上广八尺,高四尺,袤一十二丈七尺.问积几何?其意思是:现有堤坝,下底长为2丈,上底长为8尺,高4尺,纵长12丈7尺,问这段堤坝的体积是多少?在这个问题中,若某施工队的日工作量不少于350立方尺,但不超过400立方尺,则该施工队完成这段堤坝的天数不可能为( D )(注:一丈=十尺)
A.20天 B.19天 C.18天 D.16天
随堂练习
如图,网格纸上小正方形的边长为,粗实线画出的是某几何体的三视图,则该几何体的体积为( C )
A. B. C.16 D.24
感谢聆听
8.3简单几何体的表面积与体积
了解棱柱、棱锥、棱台的表面积与体积的计算公式
01
理解并掌握侧面展开图与几何体的表面积之间的关系
02
能用计算公式求几何体的表面积与体积
03
学习目标
棱柱、棱锥、棱台的表面积
01
02
03
01
棱柱、棱锥、棱台的表面积
多面体的表面积就是围成多面体各个面的面积的和,棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和
棱柱、棱锥、棱台的体积
02
02
03
02
棱柱:柱体的底面面积为S,高为h,则V=Sh
棱锥:椎体的底面面积为S,高为h,则V= Sh
棱台:台体的上、下底面面积分别为 , ,高为h,则
圆柱、圆锥、圆台的表面积
02
02
03
03
表面积
1.圆柱表面积: (r是底面半径,l是母线长)
2.圆锥表面积: = (r是底面半径,l是母线长)
3.圆台表面积: ( 分别是上、下底面半径, 是母线长)
归纳小结
01
02
03
01
圆柱、圆锥、圆台体积
02
02
03
04
体积
(1)圆柱体积: (r是底面半径,h是高)
(2)圆锥体积: (r是底面半径,h是高)
(3)圆台体积: ( 分别是上、下底面半径,是高)
名师点拨
01
02
03
01
柱体、椎体的体积公式可以看做台体体积公式的“特殊形式”
球的表面积和体积
02
02
03
05
球的表面积:
球的体积:
几个与球有关的切、接的常用理论
02
02
03
06
(1)正方体的棱长为a,球的半径为R
①若球为正方体的外接球,则2R=3a
②若球为正方体的内接球,则2R=a
③若球与正方体的各棱相切,则2R=2a
(2)若长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R=
?
例1
经典例题
围屋始建于唐宋,兴盛于明清.围屋结合了中原古朴遗风以及南方文化的地域特色,是中国五大民居特色建筑之一在形式上主要有方形围屋、半圆形围屋、圆形围屋,如图所示是墙体厚度为1m的圆形围屋(主要用泥土建筑而成,大部分是客家民居,又称客家土围楼),从地面测量内环直径是16m,外环直径是30m,墙体高10m,则该围屋所有房间的室内总体积(斜屋顶不计入室内体积及忽略房间之间的墙体厚度与楼板厚度)大约是( )
A. B. C. D.
解析
经典例题
【详解】
因为墙体厚度为1m,所以除去墙体厚度的外环直径变为(30-2)m,加上墙体厚度的内环直径变为(16+2)m,墙体高10m,由题意得围屋所有房间的室内总体积为 .
故选:D.
例2
经典例题
《九章算术》是我国古代数学名著﹐它在几何学中的研究比西方早1000多年.在《九章算术》中,将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马.如图 是阳马, 平面 , .则该阳马的外接球的表面积为( )
A. B. C. D.
解析
经典例题
【详解】
连接AC,BD,交于 ,取PC中点O,连接 ,如图所示
因为 分别为PC,AC的中点,所以 ,
又 平面ABCD,所以 平面ABCD,
所以O到A,B,C,D的距离都相等,又 ,
所以O为该四棱锥的外接球的球心,
在 中, , ,
所以 ,
所以该四棱锥的外接球的半径 ,
所以该阳马的外接球的表面积 .
故选:B
随堂练习
我国古代数学名著《九章算术》卷五“商功”中有这样一题:今有堤下广二丈,上广八尺,高四尺,袤一十二丈七尺.问积几何?其意思是:现有堤坝,下底长为2丈,上底长为8尺,高4尺,纵长12丈7尺,问这段堤坝的体积是多少?在这个问题中,若某施工队的日工作量不少于350立方尺,但不超过400立方尺,则该施工队完成这段堤坝的天数不可能为( D )(注:一丈=十尺)
A.20天 B.19天 C.18天 D.16天
随堂练习
如图,网格纸上小正方形的边长为,粗实线画出的是某几何体的三视图,则该几何体的体积为( C )
A. B. C.16 D.24
感谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
