山东省桓台第二中学2012届高三教学质量检测数学(文)试题(无答案)
文档属性
| 名称 | 山东省桓台第二中学2012届高三教学质量检测数学(文)试题(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 181.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-02 00:00:00 | ||
图片预览



文档简介
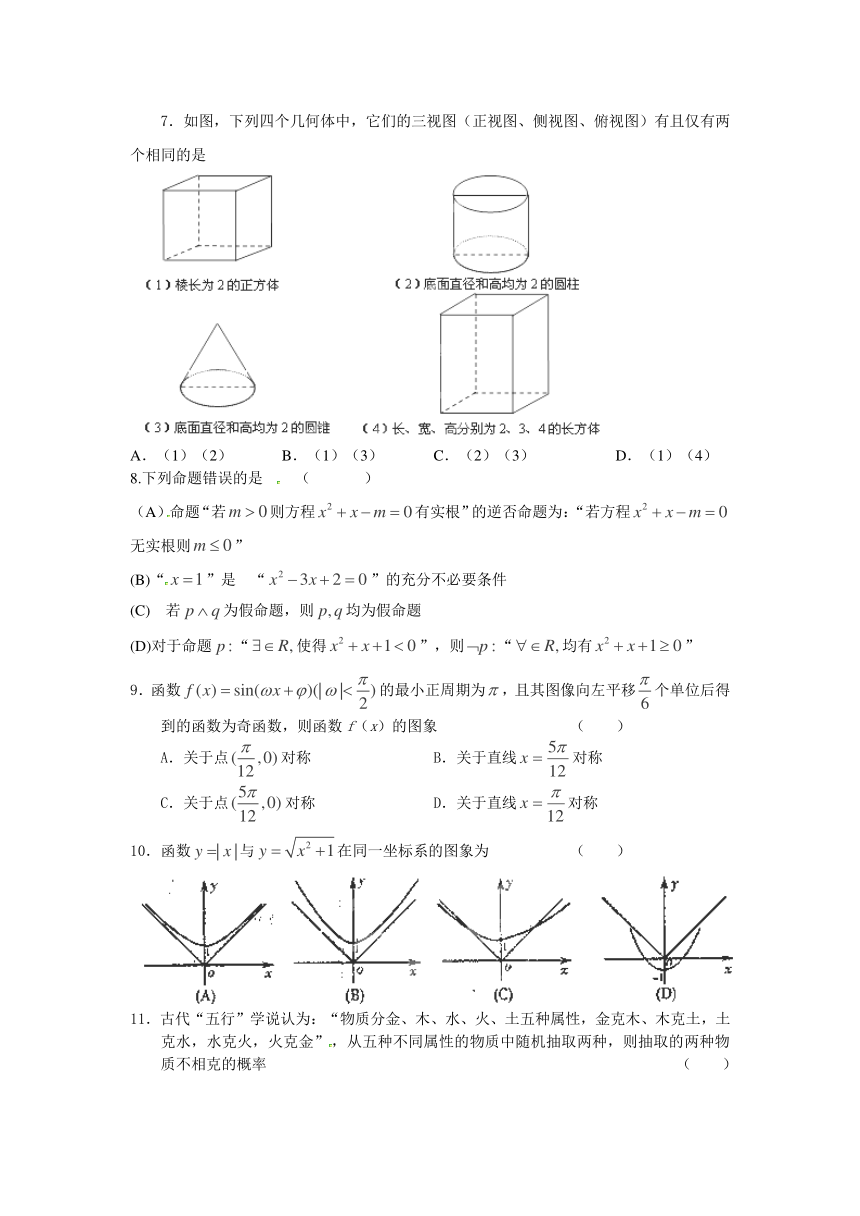
一、选择题:本大题12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若复数,则等于 ( )
A.-i B.i C.2i D.1+i
2.甲、乙两名同学在5次体育测试中的成绩统计如右面的茎叶图所示,若甲、乙两人的平均成绩分别是X甲、X乙,则下列结论正确的是 ( )
A.X甲B.X甲>X乙;甲比乙成绩稳定
C.X甲>X乙;乙比甲成绩稳定
D.X甲3.已知向量a,b均为单位向量,若它们的夹角60°,则|a-3b|等于 ( )
A. B. C. D.4
4.在下列各函数中,最小值等于2的函数是 ( )
A. B.
C. D.
5.已知圆O的方程是x2+y2—8x—2y+10=0,则过M(3,0)的最短弦所在直线方程是( )
A.x+y—3=0 B.x—y—3=0 C.2x—y—6=0 D.2x+y—6=0
6.如图所示的程序框图输出的结果是 ( )
A. B.
C. D.
7.如图,下列四个几何体中,它们的三视图(正视图、侧视图、俯视图)有且仅有两个相同的是
A.(1)(2) B.(1)(3) C.(2)(3) D.(1)(4)
8.下列命题错误的是 ( )
(A)命题“若则方程有实根”的逆否命题为:“若方程无实根则”
(B)“”是 “”的充分不必要条件
(C) 若为假命题,则均为假命题
(D)对于命题“使得”,则“均有”
9.函数的最小正周期为,且其图像向左平移个单位后得到的函数为奇函数,则函数f(x)的图象 ( )
A.关于点对称 B.关于直线对称
C.关于点对称 D.关于直线对称
10.函数与在同一坐标系的图象为 ( )
11.古代“五行”学说认为:“物质分金、木、水、火、土五种属性,金克木、木克土,土克水,水克火,火克金”,从五种不同属性的物质中随机抽取两种,则抽取的两种物质不相克的概率 ( )
A. B. C. D.
12.已知偶函数满足,且时,,则方程根的个数是
(A) 2 (B) 3 (C) 4 (D) 多于4
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.
13.已知双曲线的右焦点为,则该双曲线的渐近线方程为_________.
14.设等差数列{an}的前n项和为Sn,若,则S19=______________.
15.已知表示平面,结出下列条件:
①; ②;
③; ④
其中能推出的是 (把所有正确的条件序号都填上)
16.如图,平面上一长12cm,宽10cm的矩形ABCD内有一
半径为1cm的圆O(圆心O在矩形对角线交点处).把一
枚半径1cm的硬币任意掷在矩形内(硬币完全落在矩形内),
则硬币不与圆O相碰的概率为_________________.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17. (满分12分)
已知函数.
⑴求函数的最小正周期;
⑵求函数的最大值和最小值及相应的的值;
⑶求函数的单调增区间.
18.(本小题满分12分)
一个盒中放有除颜色不同外,其余完全相同的黑球和白球,其中黑球2个,白球3个;
(1)从盒中同时摸出两个球,求两球颜色恰好相同的概率;
(2)从盒中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
19.(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD是边长为的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=AD.
(1)求证:EF∥平面PAD;
(2)求证:平面PAB⊥平面PCD.
20.(本小题满分12分)
已知点(1,2)是函数的图象上一点,数列的前项和.
(1)求数列的通项公式;
(2)若,求数列的前项和.
21.(本小题满分12分) 已知函数f(x)=-x.
(I)当k=1时,试确定函数f(x)单调区间;
(Ⅱ)若对任意x∈R,有,f(x)>0恒成立,求实数k的取值范围.
22.(本小题满分14分)
已知椭圆C:(a>b>0)的离心率为,直线与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.
(I)求椭圆C的方程;
(II)若直线:与椭圆C交于不同的两点M,N,且线段MN的垂直平分线过定点G(,0),求实数k的取值范围.
桓台二中教学质量检测
文科数学试卷答题纸
题号 填空题 17 18 19 20 21 22 总分
得分
二:填空题(每小题4分,共计16分)
13. ; 14. ; 15. ;16. ;
三:解答题
20090526
第17题:
第18题:
第19题:
第20题:
第21题:
第22题:
1.若复数,则等于 ( )
A.-i B.i C.2i D.1+i
2.甲、乙两名同学在5次体育测试中的成绩统计如右面的茎叶图所示,若甲、乙两人的平均成绩分别是X甲、X乙,则下列结论正确的是 ( )
A.X甲
C.X甲>X乙;乙比甲成绩稳定
D.X甲
A. B. C. D.4
4.在下列各函数中,最小值等于2的函数是 ( )
A. B.
C. D.
5.已知圆O的方程是x2+y2—8x—2y+10=0,则过M(3,0)的最短弦所在直线方程是( )
A.x+y—3=0 B.x—y—3=0 C.2x—y—6=0 D.2x+y—6=0
6.如图所示的程序框图输出的结果是 ( )
A. B.
C. D.
7.如图,下列四个几何体中,它们的三视图(正视图、侧视图、俯视图)有且仅有两个相同的是
A.(1)(2) B.(1)(3) C.(2)(3) D.(1)(4)
8.下列命题错误的是 ( )
(A)命题“若则方程有实根”的逆否命题为:“若方程无实根则”
(B)“”是 “”的充分不必要条件
(C) 若为假命题,则均为假命题
(D)对于命题“使得”,则“均有”
9.函数的最小正周期为,且其图像向左平移个单位后得到的函数为奇函数,则函数f(x)的图象 ( )
A.关于点对称 B.关于直线对称
C.关于点对称 D.关于直线对称
10.函数与在同一坐标系的图象为 ( )
11.古代“五行”学说认为:“物质分金、木、水、火、土五种属性,金克木、木克土,土克水,水克火,火克金”,从五种不同属性的物质中随机抽取两种,则抽取的两种物质不相克的概率 ( )
A. B. C. D.
12.已知偶函数满足,且时,,则方程根的个数是
(A) 2 (B) 3 (C) 4 (D) 多于4
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.
13.已知双曲线的右焦点为,则该双曲线的渐近线方程为_________.
14.设等差数列{an}的前n项和为Sn,若,则S19=______________.
15.已知表示平面,结出下列条件:
①; ②;
③; ④
其中能推出的是 (把所有正确的条件序号都填上)
16.如图,平面上一长12cm,宽10cm的矩形ABCD内有一
半径为1cm的圆O(圆心O在矩形对角线交点处).把一
枚半径1cm的硬币任意掷在矩形内(硬币完全落在矩形内),
则硬币不与圆O相碰的概率为_________________.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17. (满分12分)
已知函数.
⑴求函数的最小正周期;
⑵求函数的最大值和最小值及相应的的值;
⑶求函数的单调增区间.
18.(本小题满分12分)
一个盒中放有除颜色不同外,其余完全相同的黑球和白球,其中黑球2个,白球3个;
(1)从盒中同时摸出两个球,求两球颜色恰好相同的概率;
(2)从盒中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
19.(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD是边长为的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=AD.
(1)求证:EF∥平面PAD;
(2)求证:平面PAB⊥平面PCD.
20.(本小题满分12分)
已知点(1,2)是函数的图象上一点,数列的前项和.
(1)求数列的通项公式;
(2)若,求数列的前项和.
21.(本小题满分12分) 已知函数f(x)=-x.
(I)当k=1时,试确定函数f(x)单调区间;
(Ⅱ)若对任意x∈R,有,f(x)>0恒成立,求实数k的取值范围.
22.(本小题满分14分)
已知椭圆C:(a>b>0)的离心率为,直线与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.
(I)求椭圆C的方程;
(II)若直线:与椭圆C交于不同的两点M,N,且线段MN的垂直平分线过定点G(,0),求实数k的取值范围.
桓台二中教学质量检测
文科数学试卷答题纸
题号 填空题 17 18 19 20 21 22 总分
得分
二:填空题(每小题4分,共计16分)
13. ; 14. ; 15. ;16. ;
三:解答题
20090526
第17题:
第18题:
第19题:
第20题:
第21题:
第22题:
同课章节目录
