6.3 向心加速度(基础达标)检测— 2020-2021学年【新教材】人教版(2019)高中物理必修第二册(Word版含解析)
文档属性
| 名称 | 6.3 向心加速度(基础达标)检测— 2020-2021学年【新教材】人教版(2019)高中物理必修第二册(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 497.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-24 13:35:29 | ||
图片预览




文档简介
第六章圆周运动第三节向心加速度基础达标(含解析)
一、单选题
1.在匀速圆周运动中,下列物理量不变的是( )
A.向心加速度 B.向心力 C.线速度 D.角速度
2.物体做圆周运动时,下列关于向心力和向心加速度的说法正确的是( )
A.向心力的作用是改变速度的方向
B.向心加速度大小恒定,方向时刻改变
C.物体做匀速圆周运动时,向心力是一个恒力
D.物体做非匀速圆周运动时,向心加速度的大小不可以用
来计算
3.A、B两艘快艇在湖面上做匀速圆周运动,在相同时间内,它们通过的路程之比是4∶3,运动方向改变的角度之比是3∶2,则它们( )
A.线速度大小之比为4∶3
B.角速度大小之比为3∶4
C.圆周运动的半径之比为2∶1
D.向心加速度大小之比为1∶2
4.如图所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三个轮的半径关系是。若皮带不打滑,则A、B、C三轮边缘上a、b、c三点的( )
A.角速度之比为 B.周期之比为
C.线速度之比为 D.加速度之比为
5.一个质点受到两个互成锐角的力 F1 和 F2 的作用,由静止开始运动,若运动中保持两个力的方向不变,但 F1 突然增大 ΔF,则质点此后( )
A.有可能做匀速圆周运动
B.在相等时间内速度的变化量一定相同
C.可能做变加速曲线运动
D.一定做匀变速直线运动
6.由于地球自转,比较位于赤道上的物体1与位于北纬的物体2,则( )
A.角速度之比
B.线速度之比
C.向心加速度之比
D.向心加速度之比
7.如图所示,光滑的凸轮绕O轴匀速转动,C、D是凸轮边缘上的两点,AB杆被限制在竖直方向移动,杆的下端A在O点正上方与凸轮边缘接触且被托住。凸轮位于图示位置时,AB杆正在上升。则( )
A.凸轮绕O轴逆时针方向旋转 B.凸轮上C、D两点线速度相同
C.凸轮上C、D两点角速度大小相等 D.凸轮上C、D两点向心加速度相同
8.如图所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点,左侧为一轮轴,大轮的半径为4r,小轮的半径为2r,b点在小轮上,到小轮中心距离为r,c点和d点分别位于小轮和大轮的边缘上,若在传动过程中,皮带不打滑,则( )
A.a点与c点的线速度大小相等 B.a点与b点的角速度大小相等
C.a点与b点的向心加速度大小相等。 D.a、b、c、d四点,向心加速度最小的是d点
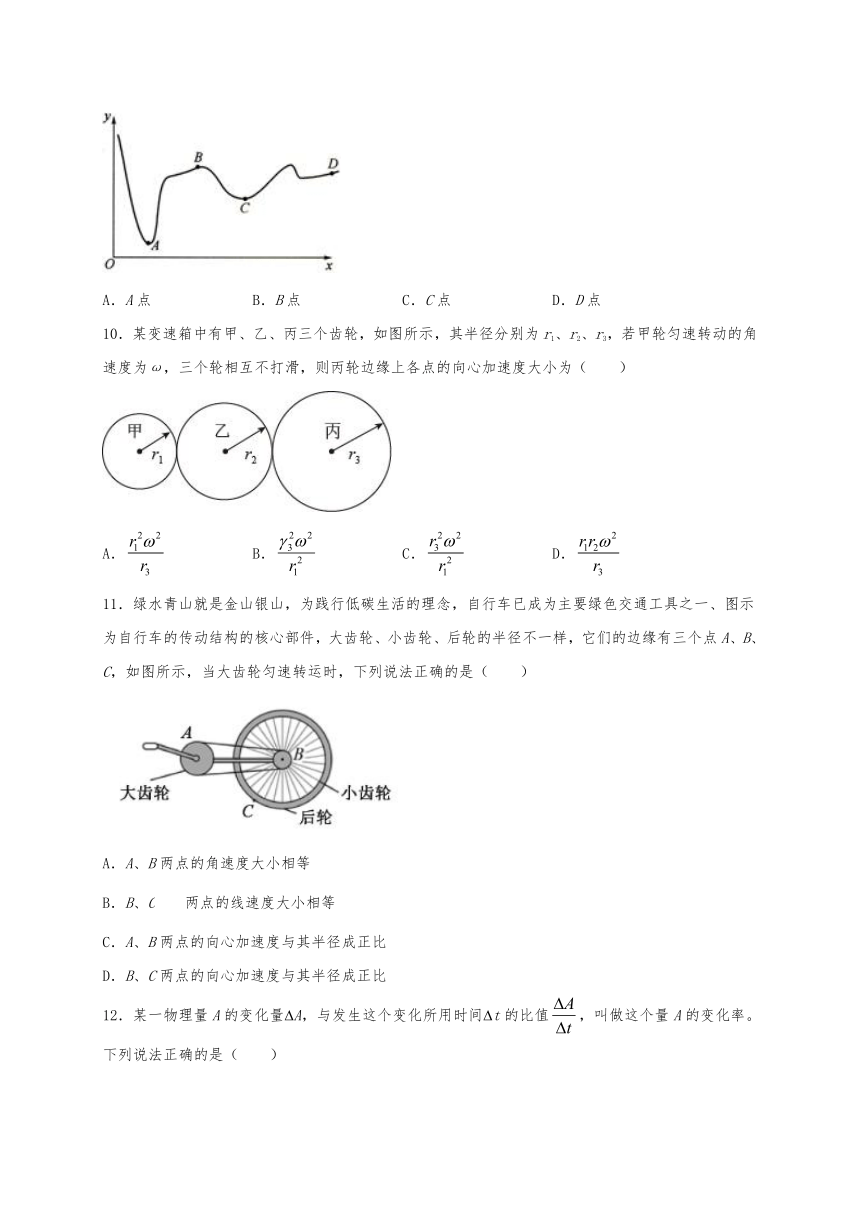
9.一质点以匀速率做曲线运动,从如图所示的轨迹可知,质点加速度最大的点是( )
A.A点 B.B点 C.C点 D.D点
10.某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮匀速转动的角速度为ω,三个轮相互不打滑,则丙轮边缘上各点的向心加速度大小为( )
A. B. C. D.
11.绿水青山就是金山银山,为践行低碳生活的理念,自行车已成为主要绿色交通工具之一、图示为自行车的传动结构的核心部件,大齿轮、小齿轮、后轮的半径不一样,它们的边缘有三个点A、B、C,如图所示,当大齿轮匀速转运时,下列说法正确的是( )
A.A、B两点的角速度大小相等
B.B、C两点的线速度大小相等
C.A、B两点的向心加速度与其半径成正比
D.B、C两点的向心加速度与其半径成正比
12.某一物理量A的变化量?A,与发生这个变化所用时间?t的比值,叫做这个量A的变化率。下列说法正确的是( )
A.若A表示某质点做匀速直线运动的位移,则是均匀增大的
B.若A表示某质点做自由落体运动下落的速度,则是恒定不变的
C.若A表示某质点做平抛运动的速度,则是均匀增大的
D.若A表示某质点做匀速圆周运动的速度,则是均匀增大的
13.如图所示是A、B两物体做匀速圆周运动的向心加速度随半径变化的图像,其中A为双曲线的一支,由图可知( )
A.A物体运动的线速度大小不变
B.A物体运动的角速度不变
C.B物体运动的角速度是变化的
D.B物体运动的线速度大小不变
14.如图所示,甲、乙两人分别站在赤道和纬度45°的地面上,则( )
A.甲的周期大 B.乙的线速度大
C.甲的角速度大 D.甲的向心加速度速度大
15.用材料和粗细相同、长短不同的两段绳子,各拴一个质量相同的小球在光滑水平面上做匀速圆周运动,那么以下说法错误的是( )
A.两个球以相同的线速度运动时,短绳易断
B.两个球以相同的角速度运动时,长绳易断
C.两个球以相同的周期运动时,长绳易断
D.两个小球以相同大小的加速度运动时,短绳易断
16.如图甲所示,用不可伸长的轻绳拴住小球,使其绕固定点O在竖直面内做圆周运动,小球经过最高点时的速度大小为v,绳子的拉力大小为,图像如图乙所示,图像中的数据a和b及重力加速度g都为已知量。以下说法正确的是( )
A.数据a与小球的质量有关
B.数据b与圆周轨道半径无关
C.的比值只与小球的质量有关,与圆周轨道半径无关
D.仅利用数据a和g能求出小球质量和圆周轨道半径
二、解答题
17.汽车保持以30m/s的速率沿半径为60m的圆形轨道匀速运动,当汽车从A运动到B时,汽车相对圆心转过的角度为90°,在这一过程中,试求:
(1) 汽车位移的大小;
(2) 汽车的角速度的大小;
(3) 汽车运动的向心加速度的大小。
18.一部机器与电动机通过皮带连接,机器皮带轮的半径是电动机皮带轮半径的3倍(图),皮带与两轮之间不发生滑动。已知机器皮带轮边缘上一点的向心加速度为0.10。
(1)电动机皮带轮与机器皮带轮的转速之比是多少?
(2)机器皮带轮上A点到转轴的距离为轮半径的一半,A点的向心加速度是多少?
(3)电动机皮带轮边缘上某点的向心加速度是多少?
19.甲、乙两物体都在做匀速圆周运动,关于以下四种情况各举一个实际的例子。在这四种情况下,哪个物体的向心加速度比较大?
A.它们的线速度大小相等,乙的半径小
B.它们的周期相等,甲的半径大
C.它们的角速度相等,乙的线速度小
D.它们的线速度大小相等,在相同时间内甲与圆心的连线扫过的角度比乙的大
参考答案
1.D
【解析】在匀速圆周运动中,向心加速度、向心力和线速度都是大小不变,方向不断变化,只有角速度不变。
故选D。
2.A
【解析】A.向心力只改变速度的方向,不改变速度的大小,A正确;
B.变速圆周运动向心加速度大小不恒定,方向时刻改变,B错误;
C.物体做匀速圆周运动时,向心力大小不变,方向时刻改变,C错误;
D.物体做圆周运动时向心加速度为
与是否是匀速圆周运动无关;
故选A。
3.A
【解析】A.时间相同,路程之比即线速度大小之比,A项正确;
B.运动方向改变的角度之比即对应扫过的圆心角之比,由于时间相同,角速度大小之比为3∶2,B项错误;
C.路程比除以角度比得半径之比,为8∶9,C项错误;
D.由向心加速度
知线速度平方比除以半径比即向心加速度大小之比,为2∶1,D项错误;
故选A。
4.D
【解析】AC.点和点是同缘传动边缘点,线速度相等,故
根据
有
点和点是同轴传动,角速度相等,故
根据
有
综合,有
故AC错误;
B.根据
则周期之比
B错误;
D.根据
可知,加速度之比为
D正确。
故选D。
5.B
【解析】BCD.质点原来是静止的,在F1、F2的合力的作用下开始运动,此时质点沿合力方向做直线运动,运动一段时间之后,物体就有了速度,而此时将F1突然增大为F1+△F,F1变大了,它们的合力也就变了,原来合力的方向与速度的方向在一条直线上,质点做的是直线运动,把F1改变之后,由平行四边形定则可知,合力的大小变了,合力的方向也变了,就不再和速度的方向在同一条直线上了,所以此后质点将做曲线运动,由于F1、F2都是恒力,改变之后它们的合力还是恒力,质点的加速度就是定值,所以质点以后做匀变速曲线运动,由△v=at知,a一定,则在相等的时间内速度的变化一定相等.故B正确,CD错误;
A.恒力作用下不可能做匀速圆周运动,选项A错误。
故选B。
6.C
【解析】A.在地球上的物体,转动的角速度、周期相同,A错误;
B.设地球半径为R,由可得,线速度之比为
B错误;
CD.由可得,向心加速度之比为
C正确,D错误。
故选C。
7.C
【解析】A.由题知,由于AB杆上升,可知A点到圆心的距离在增大,故可判断凸轮的转动方向为顺时针,故A错误;
BC.凸轮上C、D两点属于同轴转动,所以角速度相等,但它们的曲率半径不同,由
可得,线速度大小不相等,故B错误,C正确;
D.凸轮上C、D两点角速度相等,但它们的曲率半径不同,由
可得,加速度大小不相等,故D错误。
故选C。
8.A
【解析】A.由于、两点是传送带传动的两轮子边缘上两点,则
选项A正确;
BC.、两点为共轴的轮子上两点,
则
所以
则根据v=ωr可知
根据a=ωv可知
故BC错误;
D.根据可知
由上分析可知,加速度最小的是点,故D错误。
故选A。
9.A
【解析】因为质点以匀速率做曲线运动,有向心力公式
可知,曲率半径越小加速度越大,由图象可知在A点半径最小,所以加速度最大。故A正确,BCD正确。
故选A。
10.A
【解析】甲、丙的线速度大小相等,根据a=
知甲、丙的向心加速度之比为r3∶r1,甲的向心加速度a甲=r1ω2
则a丙=
故选A。
11.D
【解析】AC.AB两点在传送带上,是同缘传动的边缘点,所以两点的线速度相等,根据v=ωr,A、B两点的角速度不相等,根据
可知,A、B两点的向心加速度与其半径成反比,故AC错误;
BD.BC两点属于同轴转动,故角速度相等,线速度不等,根据
可知,B、C两点的向心加速度与其半径成正比,故B错误,D正确;
故选D。
12.B
【解析】A.若A表示某质点做匀速直线运动的位移,则表示速度,是不变的。A错误;
B.若A表示某质点做自由落体运动下落的速度,则表示加速度,是不变的,B正确;
C.若A表示某质点做平抛运动的速度,则表示加速度,是不变的,C错误;
D.若A表示某质点做匀速圆周运动的速度,则表示加速度,大小不变。D错误。
故选B。
13.A
【解析】根据an=
知,当线速度v大小为定值时,an与r成反比,其图像为双曲线的一支;根据an=rω2
知,当角速度ω大小为定值时,an与r成正比,其图像为过原点的倾斜直线。
故选A。
14.D
【解析】AC.甲、乙两人共同绕地轴随地球一起做匀速圆周运动,他们的角速度相同,根据公式
可知周期相同,故AC错误;
B.甲、乙两人共同绕地轴随地球一起做匀速圆周运动,他们的角速度相同,根据公式
v=rω
r甲>r乙
可知甲的线速度大,故B错误;
D.甲、乙两人共同绕地轴随地球一起做匀速圆周运动,他们的角速度相同,根据公式
a=ω2r
r甲>r乙
可知甲的向心加速度大,故D正确。
故选D。
15.D
【解析】A.由
可知,两球的线速度相等时,绳子越短,向心力越大,绳子的拉力越大,越容易断。A正确,不符合题意;
B.由
可知,两球的角速度相等时,绳子越长,向心力越大,绳子的拉力越大,越容易断。B正确,不符合题意;
C.由
可知,两球的周期相等时,绳子越长,向心力越大,绳子的拉力越大,越容易断。C正确,不符合题意;
D.由
可知,两球的加速度大小相等时,绳子的拉力大小相等,绳子断裂程度相同。故D错误,符合题意。
故选D。
16.B
【解析】A.当时,绳子的拉力为零,物体的重力提供向心力,有
解得
故
数据a与物体的质量无关,A错误;
B.同理,当时,有
解得
数据b与圆周轨道半径无关,B正确;
C.根据上述结果可知
的比值与小球的质量、圆周轨道半径均有关,C错误;
D.当时有
当时有
故仅利用数据a和g不能求出小球质量,D错误。
故选B。
17.(1) (2) (3)
【解析】(1) 位移是从初位置到末位置的有向线段,物体相对圆心转过的角度为90°,故位移的大小为
(2) 物体根据
可得角速度
(3) 物体运动的向心加速度的大小为
18.(1)3:1;(2)0.05m/s2;(3)0.3m/s2
【解析】(1)因电动机和机器由同一皮带连接,所以它们边缘线速度相等,设电动机半径为r1,角速度ω1,机器轮半径为r2,角速度为ω2,由题意知
根据v=rω得
即
所以
根据ω=2πn
故角速度与转速成正比,故
(2)因A与皮带边缘同轴转动,所以角速度相等,向心加速度与半径成正比,根据a=rω2
得
(3)两轮边缘的线速度相等,根据
得
得
19.见解析
【解析】A.自行车的前后齿轮,后齿轮半径小于前齿轮半径,通过链条相连,与链条接触的点线速度大小相同,根据可知,当它们的线速度相等,乙的半径小,则乙物体的向心加速度大;
B.自行车后齿轮和后轮,同轴转动,周期相同,后轮半径大,根据,可知,当它们的周期相等,甲的半径大,则甲物体的向心加速度大;
C.自行车后齿轮和后轮,同轴转动,周期相同,后齿轮边缘线速度小于后轮边沿速度,当它们的角速度相等,乙的线速度小,由v=ωr,则乙物体的半径小;根据a=ω2r,可知,当它们的角速度相等,所以乙物体的向心加速度小,即甲物体的向心加速度大;
D.自行车的前后齿轮,后齿轮半径小于前齿轮半径,通过链条相连,在相同时间内,小齿轮在相同时间内与圆心的连线扫过的角度比大齿轮的大,甲与圆心连线扫过的角度比乙大,由可知,说明甲物体的角速度大,而它们的线速度相等,根据a=ωv,可知,甲物体的向心加速度大。
一、单选题
1.在匀速圆周运动中,下列物理量不变的是( )
A.向心加速度 B.向心力 C.线速度 D.角速度
2.物体做圆周运动时,下列关于向心力和向心加速度的说法正确的是( )
A.向心力的作用是改变速度的方向
B.向心加速度大小恒定,方向时刻改变
C.物体做匀速圆周运动时,向心力是一个恒力
D.物体做非匀速圆周运动时,向心加速度的大小不可以用
来计算
3.A、B两艘快艇在湖面上做匀速圆周运动,在相同时间内,它们通过的路程之比是4∶3,运动方向改变的角度之比是3∶2,则它们( )
A.线速度大小之比为4∶3
B.角速度大小之比为3∶4
C.圆周运动的半径之比为2∶1
D.向心加速度大小之比为1∶2
4.如图所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三个轮的半径关系是。若皮带不打滑,则A、B、C三轮边缘上a、b、c三点的( )
A.角速度之比为 B.周期之比为
C.线速度之比为 D.加速度之比为
5.一个质点受到两个互成锐角的力 F1 和 F2 的作用,由静止开始运动,若运动中保持两个力的方向不变,但 F1 突然增大 ΔF,则质点此后( )
A.有可能做匀速圆周运动
B.在相等时间内速度的变化量一定相同
C.可能做变加速曲线运动
D.一定做匀变速直线运动
6.由于地球自转,比较位于赤道上的物体1与位于北纬的物体2,则( )
A.角速度之比
B.线速度之比
C.向心加速度之比
D.向心加速度之比
7.如图所示,光滑的凸轮绕O轴匀速转动,C、D是凸轮边缘上的两点,AB杆被限制在竖直方向移动,杆的下端A在O点正上方与凸轮边缘接触且被托住。凸轮位于图示位置时,AB杆正在上升。则( )
A.凸轮绕O轴逆时针方向旋转 B.凸轮上C、D两点线速度相同
C.凸轮上C、D两点角速度大小相等 D.凸轮上C、D两点向心加速度相同
8.如图所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点,左侧为一轮轴,大轮的半径为4r,小轮的半径为2r,b点在小轮上,到小轮中心距离为r,c点和d点分别位于小轮和大轮的边缘上,若在传动过程中,皮带不打滑,则( )
A.a点与c点的线速度大小相等 B.a点与b点的角速度大小相等
C.a点与b点的向心加速度大小相等。 D.a、b、c、d四点,向心加速度最小的是d点
9.一质点以匀速率做曲线运动,从如图所示的轨迹可知,质点加速度最大的点是( )
A.A点 B.B点 C.C点 D.D点
10.某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮匀速转动的角速度为ω,三个轮相互不打滑,则丙轮边缘上各点的向心加速度大小为( )
A. B. C. D.
11.绿水青山就是金山银山,为践行低碳生活的理念,自行车已成为主要绿色交通工具之一、图示为自行车的传动结构的核心部件,大齿轮、小齿轮、后轮的半径不一样,它们的边缘有三个点A、B、C,如图所示,当大齿轮匀速转运时,下列说法正确的是( )
A.A、B两点的角速度大小相等
B.B、C两点的线速度大小相等
C.A、B两点的向心加速度与其半径成正比
D.B、C两点的向心加速度与其半径成正比
12.某一物理量A的变化量?A,与发生这个变化所用时间?t的比值,叫做这个量A的变化率。下列说法正确的是( )
A.若A表示某质点做匀速直线运动的位移,则是均匀增大的
B.若A表示某质点做自由落体运动下落的速度,则是恒定不变的
C.若A表示某质点做平抛运动的速度,则是均匀增大的
D.若A表示某质点做匀速圆周运动的速度,则是均匀增大的
13.如图所示是A、B两物体做匀速圆周运动的向心加速度随半径变化的图像,其中A为双曲线的一支,由图可知( )
A.A物体运动的线速度大小不变
B.A物体运动的角速度不变
C.B物体运动的角速度是变化的
D.B物体运动的线速度大小不变
14.如图所示,甲、乙两人分别站在赤道和纬度45°的地面上,则( )
A.甲的周期大 B.乙的线速度大
C.甲的角速度大 D.甲的向心加速度速度大
15.用材料和粗细相同、长短不同的两段绳子,各拴一个质量相同的小球在光滑水平面上做匀速圆周运动,那么以下说法错误的是( )
A.两个球以相同的线速度运动时,短绳易断
B.两个球以相同的角速度运动时,长绳易断
C.两个球以相同的周期运动时,长绳易断
D.两个小球以相同大小的加速度运动时,短绳易断
16.如图甲所示,用不可伸长的轻绳拴住小球,使其绕固定点O在竖直面内做圆周运动,小球经过最高点时的速度大小为v,绳子的拉力大小为,图像如图乙所示,图像中的数据a和b及重力加速度g都为已知量。以下说法正确的是( )
A.数据a与小球的质量有关
B.数据b与圆周轨道半径无关
C.的比值只与小球的质量有关,与圆周轨道半径无关
D.仅利用数据a和g能求出小球质量和圆周轨道半径
二、解答题
17.汽车保持以30m/s的速率沿半径为60m的圆形轨道匀速运动,当汽车从A运动到B时,汽车相对圆心转过的角度为90°,在这一过程中,试求:
(1) 汽车位移的大小;
(2) 汽车的角速度的大小;
(3) 汽车运动的向心加速度的大小。
18.一部机器与电动机通过皮带连接,机器皮带轮的半径是电动机皮带轮半径的3倍(图),皮带与两轮之间不发生滑动。已知机器皮带轮边缘上一点的向心加速度为0.10。
(1)电动机皮带轮与机器皮带轮的转速之比是多少?
(2)机器皮带轮上A点到转轴的距离为轮半径的一半,A点的向心加速度是多少?
(3)电动机皮带轮边缘上某点的向心加速度是多少?
19.甲、乙两物体都在做匀速圆周运动,关于以下四种情况各举一个实际的例子。在这四种情况下,哪个物体的向心加速度比较大?
A.它们的线速度大小相等,乙的半径小
B.它们的周期相等,甲的半径大
C.它们的角速度相等,乙的线速度小
D.它们的线速度大小相等,在相同时间内甲与圆心的连线扫过的角度比乙的大
参考答案
1.D
【解析】在匀速圆周运动中,向心加速度、向心力和线速度都是大小不变,方向不断变化,只有角速度不变。
故选D。
2.A
【解析】A.向心力只改变速度的方向,不改变速度的大小,A正确;
B.变速圆周运动向心加速度大小不恒定,方向时刻改变,B错误;
C.物体做匀速圆周运动时,向心力大小不变,方向时刻改变,C错误;
D.物体做圆周运动时向心加速度为
与是否是匀速圆周运动无关;
故选A。
3.A
【解析】A.时间相同,路程之比即线速度大小之比,A项正确;
B.运动方向改变的角度之比即对应扫过的圆心角之比,由于时间相同,角速度大小之比为3∶2,B项错误;
C.路程比除以角度比得半径之比,为8∶9,C项错误;
D.由向心加速度
知线速度平方比除以半径比即向心加速度大小之比,为2∶1,D项错误;
故选A。
4.D
【解析】AC.点和点是同缘传动边缘点,线速度相等,故
根据
有
点和点是同轴传动,角速度相等,故
根据
有
综合,有
故AC错误;
B.根据
则周期之比
B错误;
D.根据
可知,加速度之比为
D正确。
故选D。
5.B
【解析】BCD.质点原来是静止的,在F1、F2的合力的作用下开始运动,此时质点沿合力方向做直线运动,运动一段时间之后,物体就有了速度,而此时将F1突然增大为F1+△F,F1变大了,它们的合力也就变了,原来合力的方向与速度的方向在一条直线上,质点做的是直线运动,把F1改变之后,由平行四边形定则可知,合力的大小变了,合力的方向也变了,就不再和速度的方向在同一条直线上了,所以此后质点将做曲线运动,由于F1、F2都是恒力,改变之后它们的合力还是恒力,质点的加速度就是定值,所以质点以后做匀变速曲线运动,由△v=at知,a一定,则在相等的时间内速度的变化一定相等.故B正确,CD错误;
A.恒力作用下不可能做匀速圆周运动,选项A错误。
故选B。
6.C
【解析】A.在地球上的物体,转动的角速度、周期相同,A错误;
B.设地球半径为R,由可得,线速度之比为
B错误;
CD.由可得,向心加速度之比为
C正确,D错误。
故选C。
7.C
【解析】A.由题知,由于AB杆上升,可知A点到圆心的距离在增大,故可判断凸轮的转动方向为顺时针,故A错误;
BC.凸轮上C、D两点属于同轴转动,所以角速度相等,但它们的曲率半径不同,由
可得,线速度大小不相等,故B错误,C正确;
D.凸轮上C、D两点角速度相等,但它们的曲率半径不同,由
可得,加速度大小不相等,故D错误。
故选C。
8.A
【解析】A.由于、两点是传送带传动的两轮子边缘上两点,则
选项A正确;
BC.、两点为共轴的轮子上两点,
则
所以
则根据v=ωr可知
根据a=ωv可知
故BC错误;
D.根据可知
由上分析可知,加速度最小的是点,故D错误。
故选A。
9.A
【解析】因为质点以匀速率做曲线运动,有向心力公式
可知,曲率半径越小加速度越大,由图象可知在A点半径最小,所以加速度最大。故A正确,BCD正确。
故选A。
10.A
【解析】甲、丙的线速度大小相等,根据a=
知甲、丙的向心加速度之比为r3∶r1,甲的向心加速度a甲=r1ω2
则a丙=
故选A。
11.D
【解析】AC.AB两点在传送带上,是同缘传动的边缘点,所以两点的线速度相等,根据v=ωr,A、B两点的角速度不相等,根据
可知,A、B两点的向心加速度与其半径成反比,故AC错误;
BD.BC两点属于同轴转动,故角速度相等,线速度不等,根据
可知,B、C两点的向心加速度与其半径成正比,故B错误,D正确;
故选D。
12.B
【解析】A.若A表示某质点做匀速直线运动的位移,则表示速度,是不变的。A错误;
B.若A表示某质点做自由落体运动下落的速度,则表示加速度,是不变的,B正确;
C.若A表示某质点做平抛运动的速度,则表示加速度,是不变的,C错误;
D.若A表示某质点做匀速圆周运动的速度,则表示加速度,大小不变。D错误。
故选B。
13.A
【解析】根据an=
知,当线速度v大小为定值时,an与r成反比,其图像为双曲线的一支;根据an=rω2
知,当角速度ω大小为定值时,an与r成正比,其图像为过原点的倾斜直线。
故选A。
14.D
【解析】AC.甲、乙两人共同绕地轴随地球一起做匀速圆周运动,他们的角速度相同,根据公式
可知周期相同,故AC错误;
B.甲、乙两人共同绕地轴随地球一起做匀速圆周运动,他们的角速度相同,根据公式
v=rω
r甲>r乙
可知甲的线速度大,故B错误;
D.甲、乙两人共同绕地轴随地球一起做匀速圆周运动,他们的角速度相同,根据公式
a=ω2r
r甲>r乙
可知甲的向心加速度大,故D正确。
故选D。
15.D
【解析】A.由
可知,两球的线速度相等时,绳子越短,向心力越大,绳子的拉力越大,越容易断。A正确,不符合题意;
B.由
可知,两球的角速度相等时,绳子越长,向心力越大,绳子的拉力越大,越容易断。B正确,不符合题意;
C.由
可知,两球的周期相等时,绳子越长,向心力越大,绳子的拉力越大,越容易断。C正确,不符合题意;
D.由
可知,两球的加速度大小相等时,绳子的拉力大小相等,绳子断裂程度相同。故D错误,符合题意。
故选D。
16.B
【解析】A.当时,绳子的拉力为零,物体的重力提供向心力,有
解得
故
数据a与物体的质量无关,A错误;
B.同理,当时,有
解得
数据b与圆周轨道半径无关,B正确;
C.根据上述结果可知
的比值与小球的质量、圆周轨道半径均有关,C错误;
D.当时有
当时有
故仅利用数据a和g不能求出小球质量,D错误。
故选B。
17.(1) (2) (3)
【解析】(1) 位移是从初位置到末位置的有向线段,物体相对圆心转过的角度为90°,故位移的大小为
(2) 物体根据
可得角速度
(3) 物体运动的向心加速度的大小为
18.(1)3:1;(2)0.05m/s2;(3)0.3m/s2
【解析】(1)因电动机和机器由同一皮带连接,所以它们边缘线速度相等,设电动机半径为r1,角速度ω1,机器轮半径为r2,角速度为ω2,由题意知
根据v=rω得
即
所以
根据ω=2πn
故角速度与转速成正比,故
(2)因A与皮带边缘同轴转动,所以角速度相等,向心加速度与半径成正比,根据a=rω2
得
(3)两轮边缘的线速度相等,根据
得
得
19.见解析
【解析】A.自行车的前后齿轮,后齿轮半径小于前齿轮半径,通过链条相连,与链条接触的点线速度大小相同,根据可知,当它们的线速度相等,乙的半径小,则乙物体的向心加速度大;
B.自行车后齿轮和后轮,同轴转动,周期相同,后轮半径大,根据,可知,当它们的周期相等,甲的半径大,则甲物体的向心加速度大;
C.自行车后齿轮和后轮,同轴转动,周期相同,后齿轮边缘线速度小于后轮边沿速度,当它们的角速度相等,乙的线速度小,由v=ωr,则乙物体的半径小;根据a=ω2r,可知,当它们的角速度相等,所以乙物体的向心加速度小,即甲物体的向心加速度大;
D.自行车的前后齿轮,后齿轮半径小于前齿轮半径,通过链条相连,在相同时间内,小齿轮在相同时间内与圆心的连线扫过的角度比大齿轮的大,甲与圆心连线扫过的角度比乙大,由可知,说明甲物体的角速度大,而它们的线速度相等,根据a=ωv,可知,甲物体的向心加速度大。
