9.2 一元一次不等式(第二课时 利用解一元一次不等式解决实际问题)课件(共19张PPT)
文档属性
| 名称 | 9.2 一元一次不等式(第二课时 利用解一元一次不等式解决实际问题)课件(共19张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 930.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 00:00:00 | ||
图片预览






文档简介
9.2 一元一次不等式
(第二课时 利用解一元一次不等式解决实际问题)
第九章 不等式与不等式组
2021年春人教版七年级(下)数学
1、会解一元一次不等式。
2、会用不等式表示实际问题中的不等关系。
掌握解一元一次不等式的步骤,会用一元一次不等式解集简单的实际问题。(重点)
寻找实际问题中的不等关系,建立数学模型。(难点)
学习目标
不等式的性质知识点回顾
不等式的两边都加上(或减去)同一个数(或式子),不等号方向不变。
表示为:如果a>b,那么a±c>b±c
不等式的两边乘(或除)同一个正数,不等号方向不变。
表示为:如果a>b,c>0,那么ac>bc (或 ????????>????????)
?
不等式的两边乘(或除)同一个负数,不等号方向发生改变。
表示为:如果a>b,c<0,那么ac?
性质一:
性质三:
性质二:
课前回顾
解一元一次不等式步骤知识点回顾
解一元一次不等式的一般步骤:
1)去分母;
2)去括号;
3)移项;
4)合并同类项;
5)未知数的系数化为1.
有些实际问题中存在不等关系,用不等式来表示这样的关系,就能把实际问题转化为数学问题,从而通过解不等式可以得到实际问题的答案。本节课我们学习利用不等式相关知识解决实际生活中出现的问题。
课前回顾
去年某城市空气质量良好(二级以上)的天数与全年天数(365天)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、根据题干内容,去年某城市空气质量良好天数为_______________天。
4、假设明年比去年至少增加x天,即不等式方程为________________ 。
明年(365天)这样的比值要超过70%
明年空气质量良好天数????????????>????????%
?
????????????×????????%
?
????????????×????????%?+????????????????>????????%
?
新课导入
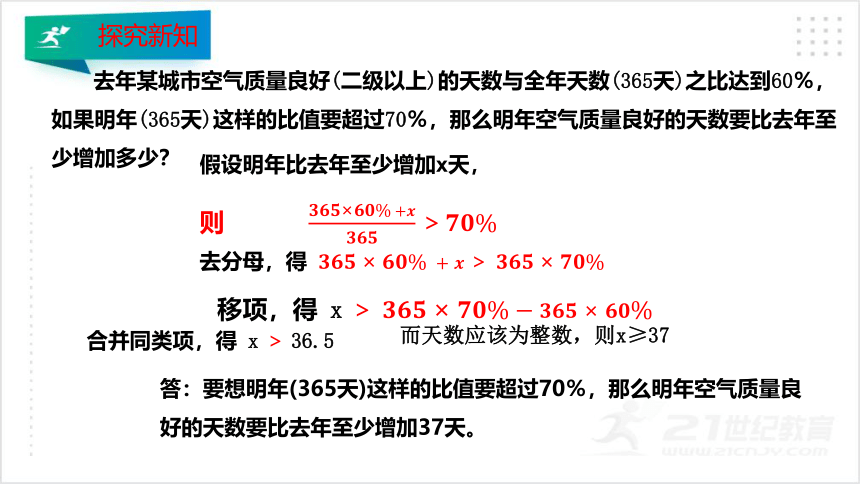
去年某城市空气质量良好(二级以上)的天数与全年天数(365天)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
假设明年比去年至少增加x天,
则 ????????????×????????%?+????????????????>????????%
?
去分母,得 ????????????×????????%?+?????> ????????????×????????%?
?
移项,得 x > ????????????×????????%?????????????×????????%
?
合并同类项,得 x >?36.5
?
而天数应该为整数,则x≥37
答:要想明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加37天。
探究新知
归纳小结
1)审:认真审题,分清已知量、未知量;
2)找:要抓住题中的关键字找出题中的不等关系;
3)设:设出适当的未知数;
4)列:根据题中的不等关系列出不等式;
5)解:解出所列不等式的解集;
6)答:检验是否符合题意,写出答案。
列不等式解应用题的基本步骤:
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
分析:
1、根据题干内容,我们需要通过三种情况讨论:
1)________________________________________。
2)________________________________________。
3)________________________________________。
累计购物金额不超过50元
累计购物金额超过50元而不超过100元
累计购物金额超过超过100元
探究新知
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
分析:2、根据题干内容,我们将三种情况购物金额填入下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
甲商场
乙商场
050x>100
x
x
x
100+0.9(x-100)
50+0.95(x-50)
50+0.95(x-50)
当消费金额不超过50元时,甲乙商场购物金额一样
到乙商场购物金额划算
购物金额超过100元时,需比较甲乙商场购物两个不等式大小
探究新知
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
购物金额超过100元时,
情况一:若在甲超市花费少,则100+0.9(x-100)<50+0.95(x-90) ,解得x>150 .
情况二:若在乙超市花费少,则100+0.9(x-100)>50+0.95(x-90) ,解得x<150 .
情况三:若在甲乙超市花费相等,则100+0.9(x-100)=50+0.95(x-90) ,
解得x=150 .
探究新知
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
综上所述,购物不超过50元和刚好是150元时,在两家商场购物没有区别;超过50元而不到150元时,在乙商场购物花费少;超过150元后,在甲商场购物花费少.
探究新知
1.已知在某超市内购物总金额超过190元时,购物总金额可按八折付款,安妮带200元到该超市买冰激凌,若冰激凌每盒9元,则她最多可买冰激凌( )盒
A.22 B.23 C.27 D.28
【分析】设最多可买x盒冰激凌,则可得不等关系:冰激凌的单价×盒数×0.8≤200,据此不难列出不等式;接下来求解该不等式就可得到x的取值范围,由实际可知x必须取整数,至此不难确定最多可买的冰激凌的盒数.
【详解】设最多可买x盒冰激凌,由题意得9x×0.8≤200,解得x≤????????????????,
∵x必须取整数,
∴x的最大整数值是27,
即她最多可以买27盒冰激凌.故选C.
?
课堂练习
2.某商店为了促销一种定价为????元的商品,采取下列方式优惠销售:若一次性购买不超过????件,则按原价付款;若一次性购买????件以上,则超过部分按原价的八折付款.如果小莹有????????元钱,那么她最多可以购买该商品( )
A.????件 B.????????件 C.????????件 D.????????件
?
【分析】购买4件需要20元,42元超过20元,则购买件数超过4件,设可以购买x件这样的商品,根据:4件按原价付款数+超过4件的总钱数≤42,列出不等式求解即可得.
【详解】∵42>4×5,∴可以购买的商品一定超过4件,
设可以购买x(x为整数)件这样的商品.4×5+(x-4)×5×0.8≤42,解得????≤????????????,
则最多可以购买该商品的件数是9,故选:A.
?
课堂练习
3.某人要完成2.1千米的路程,并要在不超过18分钟的时间内到达,已知他每分钟走90米.若跑步每分钟可跑210米,问这人完成这段路程,至少要跑( )
A.3分钟 B.4分钟 C.4.5分钟 D.5分钟
【分析】设这人跑了x分钟,则走了(18-x)分钟,根据速度×时间=路程结合要在18分钟内到达,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,取其中的最小值即可得出结论.
【详解】解:设这人跑了x分钟,则走了(18-x)分钟,
根据题意得:210x+90(18-x)≥2100,解得:x≥4,
答:这人完成这段路程,至少要跑4分钟.故选:B.
课堂练习
4.我国从2011年5月1日起在公众场所实行“禁烟”.为配合“禁烟”行动,某校组织开展了“吸烟有害健康”的知识竞赛,共有20道题.答对一题记10分,答错(或不答)一题记-5分.小明参加本次竞赛得分要超过100分,他至少要答对多少道题( ).
A.13 B.14 C.15 D.16
【分析】竞赛得分=10×答对的题数+(-5)×未答对(不答)的题数,根据本次竞赛得分要超过100分,列出不等式求解即可.
【详解】解:设要答对x道.
10x+(-5)×(20-x)>100,解得x>????????????=????????????????,
他至少要答对14道题,故选B.
?
课堂练习
5.某种商品进价为200元,标价300元出售,商场规定可以打折销售,但其利润不能少于5%.请你帮助售货员计算一下,此种商品可以按几折销售?
【分析】利润率不能低于5%,意思是利润率大于或等于5%,相应的关系式为:(打折后的销售价﹣进价)÷进价≥5%,把相关数值代入即可求解.
【详解】解:售价为300×0.1x,那么利润为300×0.1x﹣200,
所以相应的关系式为300×0.1x﹣200≥200×5%,解得:x≥7.
答:该商品最多可以7折.故答案为:7.
课堂练习
6.小明用的练习本可以到甲、乙两家商店购买,已知两商店的标价都是每本1元,甲商店的优惠条件是购买10本以上,从第11本开始按标价的70%出售;乙商店的优惠条件是,从第一本起按标价的80%出售。
(1)若设小明要购买x(x>10)本练习本,则当小明到甲商店购买时,须付款 元,当到乙商店购买时,须付款 元;
(2)买多少本练习本时,两家商店付款相同?
(3)请你给出小明购买建议。
解:(1)根据题意得,当小明到甲商店购买时,须付款:70%(x﹣10)+10=0.7x+3,当到乙商店购买时,须付款:80%x=0.8x.
故答案为:(0.7x+3),0.8x;
(2)根据题意得:0.7x+3=0.8x,解得:x=30,则买30本练习本时,两家商店付款相同;
(3)由(2)可知,当购买30本练习本时,选择哪个商店均可;
当0.7x+3>0.8x,即x<30时,去乙商店买更划算;
当0.7x+3<0.8x,即x>30时,去甲商店买更划算.
课堂练习
https://www.21cnjy.com/help/help_extract.php
(第二课时 利用解一元一次不等式解决实际问题)
第九章 不等式与不等式组
2021年春人教版七年级(下)数学
1、会解一元一次不等式。
2、会用不等式表示实际问题中的不等关系。
掌握解一元一次不等式的步骤,会用一元一次不等式解集简单的实际问题。(重点)
寻找实际问题中的不等关系,建立数学模型。(难点)
学习目标
不等式的性质知识点回顾
不等式的两边都加上(或减去)同一个数(或式子),不等号方向不变。
表示为:如果a>b,那么a±c>b±c
不等式的两边乘(或除)同一个正数,不等号方向不变。
表示为:如果a>b,c>0,那么ac>bc (或 ????????>????????)
?
不等式的两边乘(或除)同一个负数,不等号方向发生改变。
表示为:如果a>b,c<0,那么ac
性质一:
性质三:
性质二:
课前回顾
解一元一次不等式步骤知识点回顾
解一元一次不等式的一般步骤:
1)去分母;
2)去括号;
3)移项;
4)合并同类项;
5)未知数的系数化为1.
有些实际问题中存在不等关系,用不等式来表示这样的关系,就能把实际问题转化为数学问题,从而通过解不等式可以得到实际问题的答案。本节课我们学习利用不等式相关知识解决实际生活中出现的问题。
课前回顾
去年某城市空气质量良好(二级以上)的天数与全年天数(365天)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、根据题干内容,去年某城市空气质量良好天数为_______________天。
4、假设明年比去年至少增加x天,即不等式方程为________________ 。
明年(365天)这样的比值要超过70%
明年空气质量良好天数????????????>????????%
?
????????????×????????%
?
????????????×????????%?+????????????????>????????%
?
新课导入
去年某城市空气质量良好(二级以上)的天数与全年天数(365天)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
假设明年比去年至少增加x天,
则 ????????????×????????%?+????????????????>????????%
?
去分母,得 ????????????×????????%?+?????> ????????????×????????%?
?
移项,得 x > ????????????×????????%?????????????×????????%
?
合并同类项,得 x >?36.5
?
而天数应该为整数,则x≥37
答:要想明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加37天。
探究新知
归纳小结
1)审:认真审题,分清已知量、未知量;
2)找:要抓住题中的关键字找出题中的不等关系;
3)设:设出适当的未知数;
4)列:根据题中的不等关系列出不等式;
5)解:解出所列不等式的解集;
6)答:检验是否符合题意,写出答案。
列不等式解应用题的基本步骤:
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
分析:
1、根据题干内容,我们需要通过三种情况讨论:
1)________________________________________。
2)________________________________________。
3)________________________________________。
累计购物金额不超过50元
累计购物金额超过50元而不超过100元
累计购物金额超过超过100元
探究新知
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
分析:2、根据题干内容,我们将三种情况购物金额填入下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
甲商场
乙商场
0
x
x
x
100+0.9(x-100)
50+0.95(x-50)
50+0.95(x-50)
当消费金额不超过50元时,甲乙商场购物金额一样
到乙商场购物金额划算
购物金额超过100元时,需比较甲乙商场购物两个不等式大小
探究新知
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
购物金额超过100元时,
情况一:若在甲超市花费少,则100+0.9(x-100)<50+0.95(x-90) ,解得x>150 .
情况二:若在乙超市花费少,则100+0.9(x-100)>50+0.95(x-90) ,解得x<150 .
情况三:若在甲乙超市花费相等,则100+0.9(x-100)=50+0.95(x-90) ,
解得x=150 .
探究新知
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
综上所述,购物不超过50元和刚好是150元时,在两家商场购物没有区别;超过50元而不到150元时,在乙商场购物花费少;超过150元后,在甲商场购物花费少.
探究新知
1.已知在某超市内购物总金额超过190元时,购物总金额可按八折付款,安妮带200元到该超市买冰激凌,若冰激凌每盒9元,则她最多可买冰激凌( )盒
A.22 B.23 C.27 D.28
【分析】设最多可买x盒冰激凌,则可得不等关系:冰激凌的单价×盒数×0.8≤200,据此不难列出不等式;接下来求解该不等式就可得到x的取值范围,由实际可知x必须取整数,至此不难确定最多可买的冰激凌的盒数.
【详解】设最多可买x盒冰激凌,由题意得9x×0.8≤200,解得x≤????????????????,
∵x必须取整数,
∴x的最大整数值是27,
即她最多可以买27盒冰激凌.故选C.
?
课堂练习
2.某商店为了促销一种定价为????元的商品,采取下列方式优惠销售:若一次性购买不超过????件,则按原价付款;若一次性购买????件以上,则超过部分按原价的八折付款.如果小莹有????????元钱,那么她最多可以购买该商品( )
A.????件 B.????????件 C.????????件 D.????????件
?
【分析】购买4件需要20元,42元超过20元,则购买件数超过4件,设可以购买x件这样的商品,根据:4件按原价付款数+超过4件的总钱数≤42,列出不等式求解即可得.
【详解】∵42>4×5,∴可以购买的商品一定超过4件,
设可以购买x(x为整数)件这样的商品.4×5+(x-4)×5×0.8≤42,解得????≤????????????,
则最多可以购买该商品的件数是9,故选:A.
?
课堂练习
3.某人要完成2.1千米的路程,并要在不超过18分钟的时间内到达,已知他每分钟走90米.若跑步每分钟可跑210米,问这人完成这段路程,至少要跑( )
A.3分钟 B.4分钟 C.4.5分钟 D.5分钟
【分析】设这人跑了x分钟,则走了(18-x)分钟,根据速度×时间=路程结合要在18分钟内到达,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,取其中的最小值即可得出结论.
【详解】解:设这人跑了x分钟,则走了(18-x)分钟,
根据题意得:210x+90(18-x)≥2100,解得:x≥4,
答:这人完成这段路程,至少要跑4分钟.故选:B.
课堂练习
4.我国从2011年5月1日起在公众场所实行“禁烟”.为配合“禁烟”行动,某校组织开展了“吸烟有害健康”的知识竞赛,共有20道题.答对一题记10分,答错(或不答)一题记-5分.小明参加本次竞赛得分要超过100分,他至少要答对多少道题( ).
A.13 B.14 C.15 D.16
【分析】竞赛得分=10×答对的题数+(-5)×未答对(不答)的题数,根据本次竞赛得分要超过100分,列出不等式求解即可.
【详解】解:设要答对x道.
10x+(-5)×(20-x)>100,解得x>????????????=????????????????,
他至少要答对14道题,故选B.
?
课堂练习
5.某种商品进价为200元,标价300元出售,商场规定可以打折销售,但其利润不能少于5%.请你帮助售货员计算一下,此种商品可以按几折销售?
【分析】利润率不能低于5%,意思是利润率大于或等于5%,相应的关系式为:(打折后的销售价﹣进价)÷进价≥5%,把相关数值代入即可求解.
【详解】解:售价为300×0.1x,那么利润为300×0.1x﹣200,
所以相应的关系式为300×0.1x﹣200≥200×5%,解得:x≥7.
答:该商品最多可以7折.故答案为:7.
课堂练习
6.小明用的练习本可以到甲、乙两家商店购买,已知两商店的标价都是每本1元,甲商店的优惠条件是购买10本以上,从第11本开始按标价的70%出售;乙商店的优惠条件是,从第一本起按标价的80%出售。
(1)若设小明要购买x(x>10)本练习本,则当小明到甲商店购买时,须付款 元,当到乙商店购买时,须付款 元;
(2)买多少本练习本时,两家商店付款相同?
(3)请你给出小明购买建议。
解:(1)根据题意得,当小明到甲商店购买时,须付款:70%(x﹣10)+10=0.7x+3,当到乙商店购买时,须付款:80%x=0.8x.
故答案为:(0.7x+3),0.8x;
(2)根据题意得:0.7x+3=0.8x,解得:x=30,则买30本练习本时,两家商店付款相同;
(3)由(2)可知,当购买30本练习本时,选择哪个商店均可;
当0.7x+3>0.8x,即x<30时,去乙商店买更划算;
当0.7x+3<0.8x,即x>30时,去甲商店买更划算.
课堂练习
https://www.21cnjy.com/help/help_extract.php
