2020-2021学年 苏科版八年级数学下册 中心对称图形平行四边形压轴题复习(二)(Word版 含答案)
文档属性
| 名称 | 2020-2021学年 苏科版八年级数学下册 中心对称图形平行四边形压轴题复习(二)(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 179.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 00:00:00 | ||
图片预览



文档简介
中心对称图形——平行四边形
压轴题复习(二)
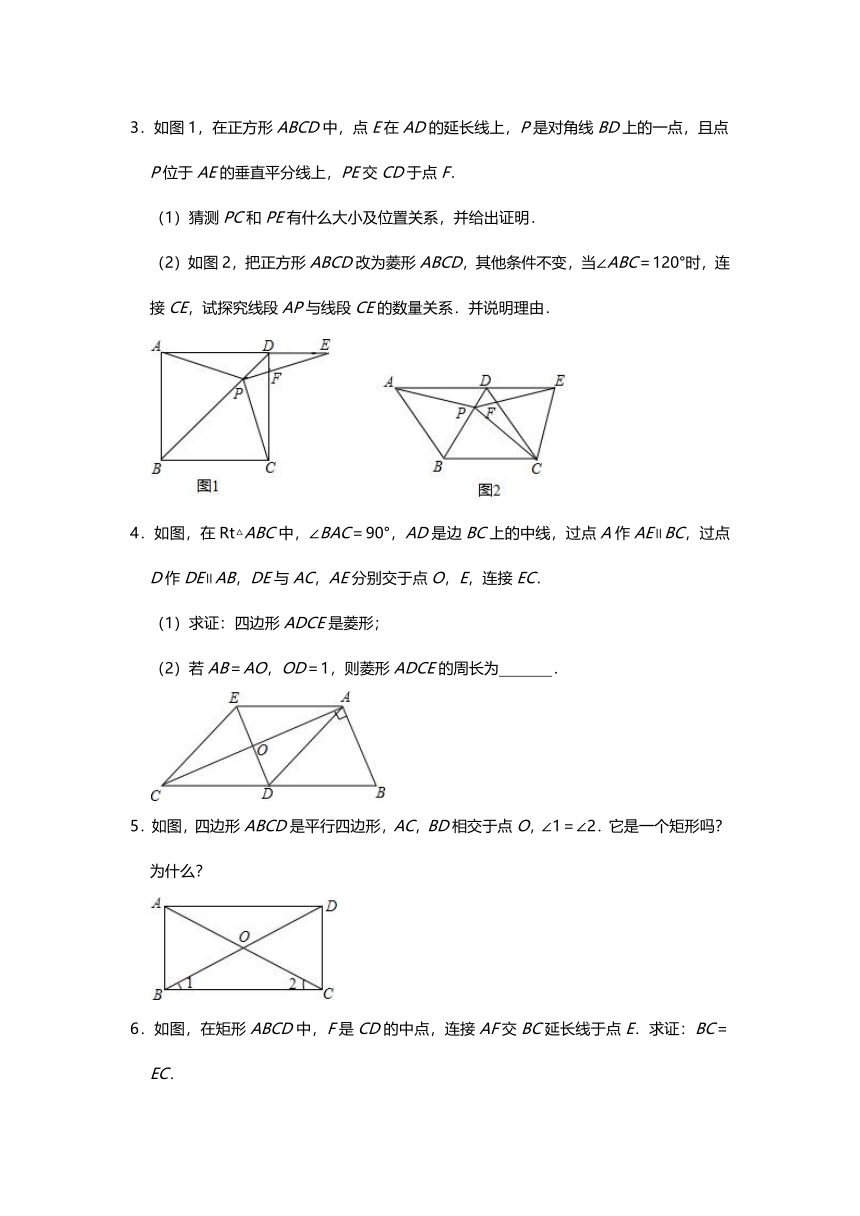
1.如图,四边形ABCD是平行四边形,E、F分别为边AB、CD的中点,连接DE、DB、BF.
(1)求证:∠DEB=∠BFD;
(2)若∠ADB=90°,证明:四边形BFDE是菱形.
2.如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB、CD边于点E、F.
(1)求证:四边形DEBF是平行四边形;
(2)当DE=DF时,求四边形DEBF的面积S四边形DEBF.
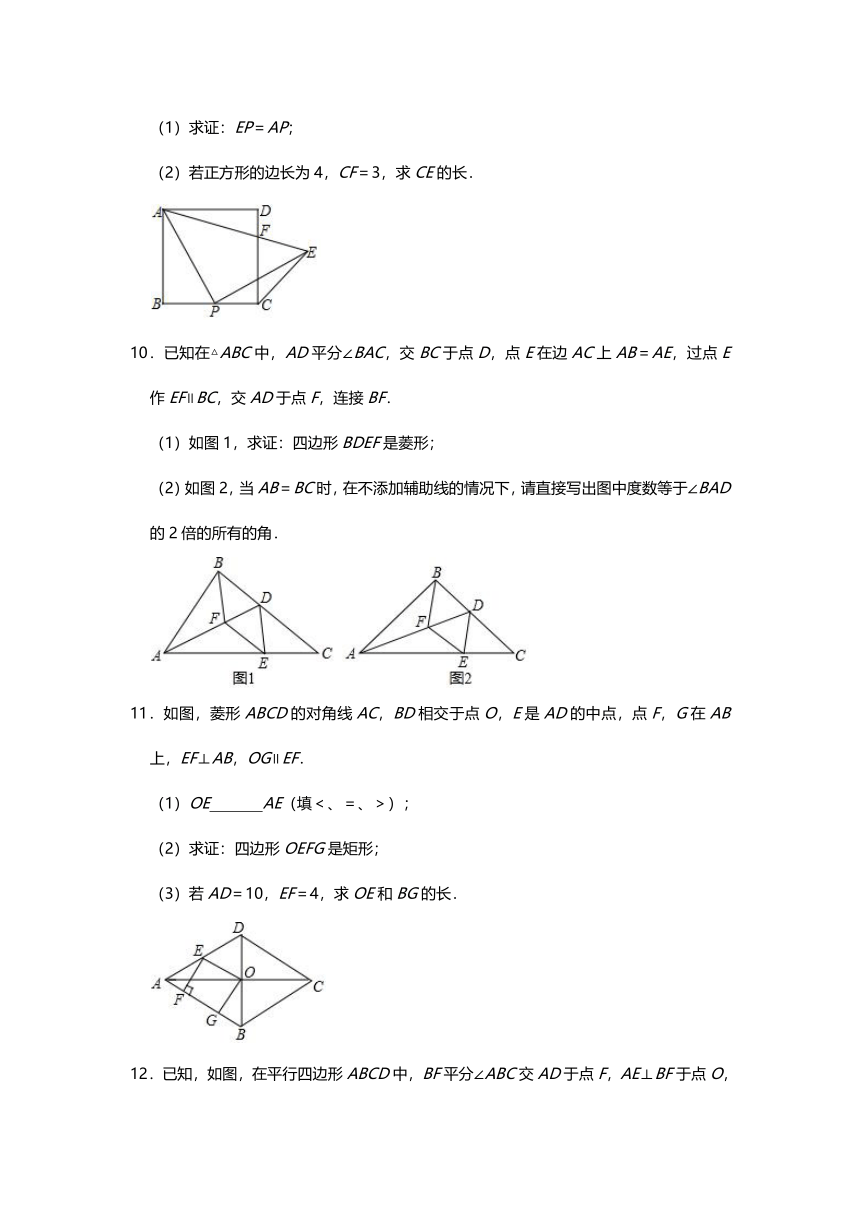
3.如图1,在正方形ABCD中,点E在AD的延长线上,P是对角线BD上的一点,且点P位于AE的垂直平分线上,PE交CD于点F.
(1)猜测PC和PE有什么大小及位置关系,并给出证明.
(2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系.并说明理由.
4.如图,在Rt△ABC中,∠BAC=90°,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC,AE分别交于点O,E,连接EC.
(1)求证:四边形ADCE是菱形;
(2)若AB=AO,OD=1,则菱形ADCE的周长为
.
5.如图,四边形ABCD是平行四边形,AC,BD相交于点O,∠1=∠2.它是一个矩形吗?为什么?
6.如图,在矩形ABCD中,F是CD的中点,连接AF交BC延长线于点E.求证:BC=EC.
7.如图,四边形ABCD为矩形,连接对角线AC,分别作∠BAC、∠BCA、∠ACD、∠DAC的角平分线AE、CE、CF、AF.
(1)当AB=BC时,求证:四边形AECF是菱形;
(2)设AB=4,BC=3,分别作EM⊥AC于点M,FN⊥AC于点N,求MN的长;
(3)分别作EG⊥BC于点G,FH⊥CD于点H,当GC=3,HC=4时,求矩形ABCD的面积.
8.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求DF的长.
9.已知P是正方形ABCD边BC上一点,连接AP,作PE⊥AP,且∠DCE=45°.若PE和CE交于E点,连接AE交CD于F.
(1)求证:EP=AP;
(2)若正方形的边长为4,CF=3,求CE的长.
10.已知在△ABC中,AD平分∠BAC,交BC于点D,点E在边AC上AB=AE,过点E作EF∥BC,交AD于点F,连接BF.
(1)如图1,求证:四边形BDEF是菱形;
(2)如图2,当AB=BC时,在不添加辅助线的情况下,请直接写出图中度数等于∠BAD的2倍的所有的角.
11.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)OE
AE(填<、=、>);
(2)求证:四边形OEFG是矩形;
(3)若AD=10,EF=4,求OE和BG的长.
12.已知,如图,在平行四边形ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若AE=12,BF=16,CE=5,求四边形ABCD的面积.
13.如图,菱形ABCD中,E为AB边上的一点,F为BC延长线上的一点,且∠BED+∠F=180°
求证:DE=DF.
14.矩形ABCD中,AB=3,BC=4.点E,F在对角线AC上,点M,N分别在边AD,BC上.
(1)如图1,若AE=CF=1,M,N分别是AD,BC的中点.求证:四边形EMFN为矩形.
(2)如图2,若AE=CF=0.5,AM=CN=x(0<x<2),且四边形EMFN为矩形,求x的值.
15.如图,在平行四边形ABCD中,线段AC的垂直平分线交AC于O,分别交BC,AD于E,F,连接AE,CF.
(1)证明:四边形AECF是菱形;
(2)在(1)的条件下,如果AC⊥AB,∠B=30°,AE=2,求四边形AECF的面积.
参考答案
1.(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB且DC∥AB,
∵E,F分别为边AB、CD上的中点,
∴DF=DC,BE=AB,且DF∥BE,
∴DF=BE且DF∥BE,
∴四边形BFDE是平行四边形,
∴∠DEB=∠BFD;
(2)证明:∵E为边AB的中点,
∴AE=BE,
∵∠ADB=90°,
∴△ADB为直角三角形
∴DE=AB=BE,
由(1)得,四边形BFDE是平行四边形,
∴平行四边形BFDE是菱形.
2.(1)证明:∵四边形ABCD是矩形,
∴DC∥AB,
∴∠FDO=∠EBO,
∵O是BD的中点,
∴DO=BO,
在△DFO和△BEO中,
,
∴△DFO≌△BEO(ASA),
∴DF=BE,
∵DC∥AB(即DF∥BE),
∴四边形DEBF是平行四边形;
(2)解:∵四边形ABCD是矩形,
∴∠A=90°,
∵AB=8,AD=6,
∴BD===10,
∵四边形DEBF是平行四边形,DE=DF,
∴四边形DEBF是菱形,
∴DE=BE,
设DE=BE=x,
在Rt△DAE中,AD2+AE2=DE2,
即62+(8﹣x)2=x2,
解得:x=,
即BE=,
∴四边形DEBF的面积S四边形DEBF=BE×AD=×6=.
3.解:(1)PC=PE,PC⊥PE
证明∵点P位于AE的垂直平分线上,
∴PA=PE,
∵四边形ABCD是正方形,
∴AB=AC,∠ADB=∠CDB,
∵PD=PD,
∴△ABP≌△CBP
(SAS)
∴PA=PC,
∴PC=PE,
∵四边形ABCD是正方形,
∴AD=CD,∠ADP=∠CBP,
∵PB=PB,
∴△ADP≌△CDP
(SAS),
∴∠PAD=∠PCD,
∵PA=PE,
∴∠PAD=∠E,
∴∠PCD=∠E,
∵∠PFC=∠DFE,
∴△CPF∽△EDF,
∴∠CPF=∠FDE,
∵四边形ABCD是正方形,
,∴∠ADC=90°,
∴∠FDE=90°,
∴∠CPF=90°,
∴PC⊥PE.
(2)PA=CE.理由如下:
证明:∵点P位于AE的垂直平分线上,
∴PA=PE,
∵四边形ABCD是菱形,
∴AB=AC,∠ADB=∠CDB,
∵PD=PD,
∴△ABP≌△CBP,
∴PA=PC
∴PC=PE,
∵四边形ABCD是菱形,
∴AD=CD,∠ADP=∠CBP,
∵PB=PB,
∴△ADP≌△CDP,
∴∠PAD=∠PCD,
∵PA=PE,
∴∠PAD=∠PED,
∴∠PCD=∠PED,
∵∠PFC=∠DFE,
∴△CPF∽△EDF,
∴∠CPF=∠EDF,
∵四边形ABCD是菱形,∠ABC=120°
∴∠ADC=∠ABC=120°
∴∠EDF=180°﹣∠ADC=60°
∴∠CPF=60°
∵PE=PC
∴△PCE是等边三角形
∴CE=PE
∴AP=CE.
4.(1)证明:∵AE∥BC,DE∥AB,
∴四边形ABDE为平行四边形,
∴AE=BD,
∵AD是边BC上的中线,
∴BD=CD,
∴AE=CD,
∴四边形ADCE是平行四边形,
又∵∠BAC=90°,AD是边BC上的中线,
∴AD=BC=CD,
∴平行四边形ADCE是菱形;
(2)解:∵四边形ADCE是菱形,
∴AD=AE=CE=CD,AC⊥DE,OA=OC,
∵BD=CD,
∴OD是△ABC的中位线,
∴AB=2OD=2,
∴AO=AB=2,
∴AD===,
∴菱形ADCE的周长=4AD=4,
故答案为:4.
5.解:四边形ABCD是矩形.理由如下:
证明:如图,∵四边形ABCD是平行四边形,
∴OC=AC,OB=BD.
又∵∠1=∠2,
∴OB=OC,
∴BD=AC,
∴?ABCD是矩形.
6.证明:∵四边形ABCD是矩形,
∴AD∥BE,AD=BC,
∴∠ADF=∠ECF,∠DAF=∠CEF,
∵F是CD的中点,
∴DF=CF,
∴在△ADF和△ECF中,
∴△ADF≌△ECF(AAS).
∴AD=EC,而AD=BC
∴BC=EC.
7.解:(1)∵四边形ABCD为矩形,
∴AB∥CD,
∴∠BAC=∠DCA,
∵AE平分∠BAC,CF平分∠ACD,
∴∠EAC=∠FCA,
∴AE∥CF,
同理,AF∥CE,
∴四边形AECF是平行四边形,
∵AB=BC,
∴∠BAC=∠ACB,
∵AE平分∠BAC,CE平分∠ACB,
∴∠EAC=∠ECA,
∴AE=CE,
∴四边形AECF是菱形;
(2)过E作EH⊥BC于点H,EG⊥AB于点G,
∵∠B=90°,
∴四边形BHEG为矩形,
∵AE平分∠BAC,CE平分∠ACB,
∴EM=EG=EH,
∴四边形BHEG是正方形,
∴BG=BH,
∵EM=EG=EH,AE=AE,CE=CE,
∴Rt△AEG≌Rt△AEM(HL),Rt△CEH≌Rt△CEM(HL),
∴AM=AG,CM=CH,
∵AB=4,BC=3,
∴AC=5,
设AM=AG=x,CM=CH=y,BH=BG=z,则
,
解得,,
∴AM=3,CM=2,
∵由(1)知四边形AECF是平行四边形,
∴AF=CE,AF∥CE,
∴∠FAN=∠ECM,
∵∠ANF=∠CME=90°,
∴△ANF≌△CME(AAS),
∴AN=CM=2,
∴MN=AM﹣AN=3﹣2=1;
(3)过E作EK⊥AB于点K,EL⊥AC于点L,如图,
∵矩形ABCD中AB∥CD,
∴∠BAC=∠ACD,
∵AE、CF分别平分∠BAC和∠ACD,
∴∠KAE=∠HCF,
∵四边形AECF是平行四边形,
∴AE=CF,
∵∠AKE=∠CHF=90°,
∴△AEK≌△CHF(AAS),
∴AK=CH=4,
∵AE平分∠BAC,CE平分∠ACB,
∴EK=EL=EG,
∵AE=AE,CE=CE,
∴Rt△AEK≌Rt△AEL(HL),Rt△CEG≌Rt△CEL(HL),
∴AK=AL=4,CG=CL=3,
∴AC=AL+CL=4+3=7,
∵EK=EG,∠EKB=∠B=∠EGB=90°,
∴四边形BGEK为正方形,
∴BG=BK,
∴矩形ABCD的面积=AB?BC=24.
8.(1)证明:∵四边形ABCD是矩形,O是BD的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF,
∴△BOE≌△DOF(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形;
(2)解:当四边形BEDF是菱形时,BD⊥EF,
设BE=x,则
DE=x,AE=6﹣x,
在Rt△ADE中,DE2=AD2+AE2,
∴x2=42+(6﹣x)2,
解得:x=,
∵DF=.
9(1)证明:连接AC,过P点作PG⊥BC交AC于G点,
∵四边形ABCD是正方形,
∴∠ACB=45°,∠BCD=90°,
∵PG⊥BC,
∴∠GPC=90°,
∴∠PGC=45°,
∴PG=PC,
∵∠DCE=45°,
∴∠AGP=∠ECP=90°+45°=135°,
∵AP⊥PE,
∴∠APE=∠GPC=90°,
∴∠APG=∠EPC=90°﹣∠GPE,
在△PAG和△PEC中
∴△PAG≌△PEC(ASA),
∴PE=PA;
(2)解:延长CB到Q,使BQ=DF,过E作EH⊥BC,EH交BC延长线于H,连接AQ,PF,
∵四边形ABCD是正方形,
∴∠D=∠DAB=∠ABC=90°,AD=AB,
∴∠ABQ=∠D=90°,
在△ABQ和△ADF中
∴△ABQ≌△ADF(SAS),
∴AQ=AF,∠DAF=∠QAB,
∵∠APE=90°,AP=PE,
∴∠PAE=∠AEP=45°,
∴∠AQP=∠QAB+∠BAP=∠DAF+∠BAP=∠DAB﹣∠PAE=90°﹣45°=45°=∠PAE,
在△QAP和△FAP中
∴△QAP≌△FAP(SAS),
∴QP=PE,
∵EH⊥BC,∠ABP=90°,∠APE=90°,
∴∠ABP=∠H=90°,∠APB=∠PEH=90°﹣∠EPH,
在△PEH和△APB中
∴△PEH≌△APB(AAS),
∴BP=EH,
∵∠H=90°,∠DCE=45°,
∴∠ECH=45°=∠CEH,
∴CH=EH=BP,
设EH=CH=BP=x,
∴PC=4﹣x,PF=BQ+BP=DF+BP=4﹣3+x=1+x,
在Rt△PCF中,由勾股定理得:(1+x)2=(4﹣x)2+32,
解之得:x=,
即CH=EH=,
∴在Rt△CHE中,由勾股定理得:CE=CH=.
10.解:(1)证明:∵AD平分∠BAC,
∴∠BAD=∠EAD,
∵AB=AE,AD=AD,
∴△ABD≌△AED(SAS),
∴DB=DE,∠BDA=∠EDA.
∵EF∥BC,
∴∠EFD=∠BDA,
∴∠EFD=∠EDF,
∴EF=ED,
∴EF=BD,
∵EF∥BD,
∴四边形BDEF为菱形.
(2)∵AD平分∠BAC,
∴∠BAC=2∠BAD,
∵AB=BC,
∴∠BAC=∠BCA=2∠BAD,
∵EF∥BC,
∴∠FEC=∠BCA=2∠BAD,
∵∠ABF=∠AEF,
∴∠ABF=2∠BAD.
所以图中度数等于∠BAD的2倍的所有的角:
∠BAC,∠BCA,∠ABF,∠AEF.
11.(1)解:∵四边形ABCD是菱形,
∴AC⊥BD,
∵E是AD的中点,
∴OE=AD=AE,
故答案为:=;
(2)证明:∵四边形ABCD是菱形,
∴OB=OD,
∵E是AD的中点,
∴OE是△ABD的中位线,
∴OE∥FG,
∵OG∥EF,
∴四边形OEFG是平行四边形,
∵EF⊥AB,
∴∠EFG=90°,
∴平行四边形OEFG是矩形;
(3)解:∵四边形ABCD是菱形,
∴BD⊥AC,AB=AD=10,
∴∠AOD=90°,
∵E是AD的中点,
∴OE=AE=AD=5;
由(1)知,四边形OEFG是矩形,
∴FG=OE=5,
∵AE=5,EF=4,
∴AF===3,
∴BG=AB﹣AF﹣FG=10﹣3﹣5=2.
12.解:(1)证明:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AFB=∠FBE,
∵BF平分∠ABC,
∴∠ABF=∠EBF,
∴∠AFB=∠ABF,
∴AF=AB,
∵AE⊥BF,
∴∠AOB=∠EOB=90°,
OB=OB,
∠ABO=∠EBO,
∴△ABO≌△EBO(ASA),
∴AB=BE,
∴AF=BE,
又AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=BE,
∴平行四边形ABEF是菱形.
(2)如图,作AG⊥BC于点G,
∵四边形ABEF是菱形,
OA=OE=AE=6,
OB=OF=BF=8,
∴AB==10,
BE=10,
设BG=x,则EG=BE﹣BG=10﹣x,
∴在Rt△ABG和Rt△AEG中,
根据勾股定理,得AG2=AB2﹣BG2=AE2﹣EG2
即102﹣x2=122﹣(10﹣x)2
解得x=,
∴AG==.
∴四边形ABCD的面积为:BC?AG=15×=144.
13.解:如图,过点D作DN⊥AB于N,DM⊥BC于F,
∵四边形ABCD是菱形,
∴AB=BC,
∵S菱形ABCD=AB×DN=BC×DM,
∴DN=DM,
∵∠BED+∠F=180°,∠BED+∠AED=180°,
∴∠F=∠AED,
又∵∠DNE=∠DMF,
∴△DNE≌△DMF(AAS)
∴DE=DF.
14.(1)证明:连接MN,如图1所示:
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠B=90°,
∴∠EAM=∠FCN,AC===5,
∵M,N分别是AD,BC的中点,
∴AM=DM=BN=CN,AM∥BN,
∴四边形ABNM是平行四边形,
又∵∠B=90°,
∴四边形ABNM是矩形,
∴MN=AB=3,
在△AME和△CNF中,,
∴△AME≌△CNF(SAS),
∴EM=FN,∠AEM=∠CFN,
∴∠MEF=∠NFE,
∴EM∥FN,
∴四边形EMFN是平行四边形,
又∵AE=CF=1,
∴EF=AC﹣AE﹣CF=3,
∴MN=EF,
∴四边形EMFN为矩形.
(2)解:连接MN,作MH⊥BC于H,如图2所示:
则四边形ABHM是矩形,
∴MH=AB=3,BH=AM=x,
∴HN=BC﹣BH﹣CN=4﹣2x,
∵四边形EMFN为矩形,AE=CF=0.5,
∴MN=EF=AC﹣AE﹣CF=4,
在Rt△MHN中,由勾股定理得:32+(4﹣2x)2=42,
∴x=2﹣.
15.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠OAF=∠OCE,
∵EF是线段AC的垂直平分线,
∴OA=OC,EF⊥AC,
在△AOF和△COE中,,
∴△AOF≌△COE(ASA),
∴AF=CE,
∴四边形AECF是平行四边形,
又∵EF⊥AC,
∴四边形AECF是菱形;
(2)解:由(1)得:四边形AECF是菱形,EF⊥AC,
∴CE=AE=2,OA=OC,OB=OD,
∵AC⊥AB,
∴EF∥AB,
∴∠OEC=∠B=30°,
∴OC=CE=1,OE=OC=,
∴AC=2OC=2,EF=2OE=2,
∴四边形AECF的面积=AC×EF=×2×2=2.
压轴题复习(二)
1.如图,四边形ABCD是平行四边形,E、F分别为边AB、CD的中点,连接DE、DB、BF.
(1)求证:∠DEB=∠BFD;
(2)若∠ADB=90°,证明:四边形BFDE是菱形.
2.如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB、CD边于点E、F.
(1)求证:四边形DEBF是平行四边形;
(2)当DE=DF时,求四边形DEBF的面积S四边形DEBF.
3.如图1,在正方形ABCD中,点E在AD的延长线上,P是对角线BD上的一点,且点P位于AE的垂直平分线上,PE交CD于点F.
(1)猜测PC和PE有什么大小及位置关系,并给出证明.
(2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系.并说明理由.
4.如图,在Rt△ABC中,∠BAC=90°,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC,AE分别交于点O,E,连接EC.
(1)求证:四边形ADCE是菱形;
(2)若AB=AO,OD=1,则菱形ADCE的周长为
.
5.如图,四边形ABCD是平行四边形,AC,BD相交于点O,∠1=∠2.它是一个矩形吗?为什么?
6.如图,在矩形ABCD中,F是CD的中点,连接AF交BC延长线于点E.求证:BC=EC.
7.如图,四边形ABCD为矩形,连接对角线AC,分别作∠BAC、∠BCA、∠ACD、∠DAC的角平分线AE、CE、CF、AF.
(1)当AB=BC时,求证:四边形AECF是菱形;
(2)设AB=4,BC=3,分别作EM⊥AC于点M,FN⊥AC于点N,求MN的长;
(3)分别作EG⊥BC于点G,FH⊥CD于点H,当GC=3,HC=4时,求矩形ABCD的面积.
8.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求DF的长.
9.已知P是正方形ABCD边BC上一点,连接AP,作PE⊥AP,且∠DCE=45°.若PE和CE交于E点,连接AE交CD于F.
(1)求证:EP=AP;
(2)若正方形的边长为4,CF=3,求CE的长.
10.已知在△ABC中,AD平分∠BAC,交BC于点D,点E在边AC上AB=AE,过点E作EF∥BC,交AD于点F,连接BF.
(1)如图1,求证:四边形BDEF是菱形;
(2)如图2,当AB=BC时,在不添加辅助线的情况下,请直接写出图中度数等于∠BAD的2倍的所有的角.
11.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)OE
AE(填<、=、>);
(2)求证:四边形OEFG是矩形;
(3)若AD=10,EF=4,求OE和BG的长.
12.已知,如图,在平行四边形ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若AE=12,BF=16,CE=5,求四边形ABCD的面积.
13.如图,菱形ABCD中,E为AB边上的一点,F为BC延长线上的一点,且∠BED+∠F=180°
求证:DE=DF.
14.矩形ABCD中,AB=3,BC=4.点E,F在对角线AC上,点M,N分别在边AD,BC上.
(1)如图1,若AE=CF=1,M,N分别是AD,BC的中点.求证:四边形EMFN为矩形.
(2)如图2,若AE=CF=0.5,AM=CN=x(0<x<2),且四边形EMFN为矩形,求x的值.
15.如图,在平行四边形ABCD中,线段AC的垂直平分线交AC于O,分别交BC,AD于E,F,连接AE,CF.
(1)证明:四边形AECF是菱形;
(2)在(1)的条件下,如果AC⊥AB,∠B=30°,AE=2,求四边形AECF的面积.
参考答案
1.(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB且DC∥AB,
∵E,F分别为边AB、CD上的中点,
∴DF=DC,BE=AB,且DF∥BE,
∴DF=BE且DF∥BE,
∴四边形BFDE是平行四边形,
∴∠DEB=∠BFD;
(2)证明:∵E为边AB的中点,
∴AE=BE,
∵∠ADB=90°,
∴△ADB为直角三角形
∴DE=AB=BE,
由(1)得,四边形BFDE是平行四边形,
∴平行四边形BFDE是菱形.
2.(1)证明:∵四边形ABCD是矩形,
∴DC∥AB,
∴∠FDO=∠EBO,
∵O是BD的中点,
∴DO=BO,
在△DFO和△BEO中,
,
∴△DFO≌△BEO(ASA),
∴DF=BE,
∵DC∥AB(即DF∥BE),
∴四边形DEBF是平行四边形;
(2)解:∵四边形ABCD是矩形,
∴∠A=90°,
∵AB=8,AD=6,
∴BD===10,
∵四边形DEBF是平行四边形,DE=DF,
∴四边形DEBF是菱形,
∴DE=BE,
设DE=BE=x,
在Rt△DAE中,AD2+AE2=DE2,
即62+(8﹣x)2=x2,
解得:x=,
即BE=,
∴四边形DEBF的面积S四边形DEBF=BE×AD=×6=.
3.解:(1)PC=PE,PC⊥PE
证明∵点P位于AE的垂直平分线上,
∴PA=PE,
∵四边形ABCD是正方形,
∴AB=AC,∠ADB=∠CDB,
∵PD=PD,
∴△ABP≌△CBP
(SAS)
∴PA=PC,
∴PC=PE,
∵四边形ABCD是正方形,
∴AD=CD,∠ADP=∠CBP,
∵PB=PB,
∴△ADP≌△CDP
(SAS),
∴∠PAD=∠PCD,
∵PA=PE,
∴∠PAD=∠E,
∴∠PCD=∠E,
∵∠PFC=∠DFE,
∴△CPF∽△EDF,
∴∠CPF=∠FDE,
∵四边形ABCD是正方形,
,∴∠ADC=90°,
∴∠FDE=90°,
∴∠CPF=90°,
∴PC⊥PE.
(2)PA=CE.理由如下:
证明:∵点P位于AE的垂直平分线上,
∴PA=PE,
∵四边形ABCD是菱形,
∴AB=AC,∠ADB=∠CDB,
∵PD=PD,
∴△ABP≌△CBP,
∴PA=PC
∴PC=PE,
∵四边形ABCD是菱形,
∴AD=CD,∠ADP=∠CBP,
∵PB=PB,
∴△ADP≌△CDP,
∴∠PAD=∠PCD,
∵PA=PE,
∴∠PAD=∠PED,
∴∠PCD=∠PED,
∵∠PFC=∠DFE,
∴△CPF∽△EDF,
∴∠CPF=∠EDF,
∵四边形ABCD是菱形,∠ABC=120°
∴∠ADC=∠ABC=120°
∴∠EDF=180°﹣∠ADC=60°
∴∠CPF=60°
∵PE=PC
∴△PCE是等边三角形
∴CE=PE
∴AP=CE.
4.(1)证明:∵AE∥BC,DE∥AB,
∴四边形ABDE为平行四边形,
∴AE=BD,
∵AD是边BC上的中线,
∴BD=CD,
∴AE=CD,
∴四边形ADCE是平行四边形,
又∵∠BAC=90°,AD是边BC上的中线,
∴AD=BC=CD,
∴平行四边形ADCE是菱形;
(2)解:∵四边形ADCE是菱形,
∴AD=AE=CE=CD,AC⊥DE,OA=OC,
∵BD=CD,
∴OD是△ABC的中位线,
∴AB=2OD=2,
∴AO=AB=2,
∴AD===,
∴菱形ADCE的周长=4AD=4,
故答案为:4.
5.解:四边形ABCD是矩形.理由如下:
证明:如图,∵四边形ABCD是平行四边形,
∴OC=AC,OB=BD.
又∵∠1=∠2,
∴OB=OC,
∴BD=AC,
∴?ABCD是矩形.
6.证明:∵四边形ABCD是矩形,
∴AD∥BE,AD=BC,
∴∠ADF=∠ECF,∠DAF=∠CEF,
∵F是CD的中点,
∴DF=CF,
∴在△ADF和△ECF中,
∴△ADF≌△ECF(AAS).
∴AD=EC,而AD=BC
∴BC=EC.
7.解:(1)∵四边形ABCD为矩形,
∴AB∥CD,
∴∠BAC=∠DCA,
∵AE平分∠BAC,CF平分∠ACD,
∴∠EAC=∠FCA,
∴AE∥CF,
同理,AF∥CE,
∴四边形AECF是平行四边形,
∵AB=BC,
∴∠BAC=∠ACB,
∵AE平分∠BAC,CE平分∠ACB,
∴∠EAC=∠ECA,
∴AE=CE,
∴四边形AECF是菱形;
(2)过E作EH⊥BC于点H,EG⊥AB于点G,
∵∠B=90°,
∴四边形BHEG为矩形,
∵AE平分∠BAC,CE平分∠ACB,
∴EM=EG=EH,
∴四边形BHEG是正方形,
∴BG=BH,
∵EM=EG=EH,AE=AE,CE=CE,
∴Rt△AEG≌Rt△AEM(HL),Rt△CEH≌Rt△CEM(HL),
∴AM=AG,CM=CH,
∵AB=4,BC=3,
∴AC=5,
设AM=AG=x,CM=CH=y,BH=BG=z,则
,
解得,,
∴AM=3,CM=2,
∵由(1)知四边形AECF是平行四边形,
∴AF=CE,AF∥CE,
∴∠FAN=∠ECM,
∵∠ANF=∠CME=90°,
∴△ANF≌△CME(AAS),
∴AN=CM=2,
∴MN=AM﹣AN=3﹣2=1;
(3)过E作EK⊥AB于点K,EL⊥AC于点L,如图,
∵矩形ABCD中AB∥CD,
∴∠BAC=∠ACD,
∵AE、CF分别平分∠BAC和∠ACD,
∴∠KAE=∠HCF,
∵四边形AECF是平行四边形,
∴AE=CF,
∵∠AKE=∠CHF=90°,
∴△AEK≌△CHF(AAS),
∴AK=CH=4,
∵AE平分∠BAC,CE平分∠ACB,
∴EK=EL=EG,
∵AE=AE,CE=CE,
∴Rt△AEK≌Rt△AEL(HL),Rt△CEG≌Rt△CEL(HL),
∴AK=AL=4,CG=CL=3,
∴AC=AL+CL=4+3=7,
∵EK=EG,∠EKB=∠B=∠EGB=90°,
∴四边形BGEK为正方形,
∴BG=BK,
∴矩形ABCD的面积=AB?BC=24.
8.(1)证明:∵四边形ABCD是矩形,O是BD的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF,
∴△BOE≌△DOF(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形;
(2)解:当四边形BEDF是菱形时,BD⊥EF,
设BE=x,则
DE=x,AE=6﹣x,
在Rt△ADE中,DE2=AD2+AE2,
∴x2=42+(6﹣x)2,
解得:x=,
∵DF=.
9(1)证明:连接AC,过P点作PG⊥BC交AC于G点,
∵四边形ABCD是正方形,
∴∠ACB=45°,∠BCD=90°,
∵PG⊥BC,
∴∠GPC=90°,
∴∠PGC=45°,
∴PG=PC,
∵∠DCE=45°,
∴∠AGP=∠ECP=90°+45°=135°,
∵AP⊥PE,
∴∠APE=∠GPC=90°,
∴∠APG=∠EPC=90°﹣∠GPE,
在△PAG和△PEC中
∴△PAG≌△PEC(ASA),
∴PE=PA;
(2)解:延长CB到Q,使BQ=DF,过E作EH⊥BC,EH交BC延长线于H,连接AQ,PF,
∵四边形ABCD是正方形,
∴∠D=∠DAB=∠ABC=90°,AD=AB,
∴∠ABQ=∠D=90°,
在△ABQ和△ADF中
∴△ABQ≌△ADF(SAS),
∴AQ=AF,∠DAF=∠QAB,
∵∠APE=90°,AP=PE,
∴∠PAE=∠AEP=45°,
∴∠AQP=∠QAB+∠BAP=∠DAF+∠BAP=∠DAB﹣∠PAE=90°﹣45°=45°=∠PAE,
在△QAP和△FAP中
∴△QAP≌△FAP(SAS),
∴QP=PE,
∵EH⊥BC,∠ABP=90°,∠APE=90°,
∴∠ABP=∠H=90°,∠APB=∠PEH=90°﹣∠EPH,
在△PEH和△APB中
∴△PEH≌△APB(AAS),
∴BP=EH,
∵∠H=90°,∠DCE=45°,
∴∠ECH=45°=∠CEH,
∴CH=EH=BP,
设EH=CH=BP=x,
∴PC=4﹣x,PF=BQ+BP=DF+BP=4﹣3+x=1+x,
在Rt△PCF中,由勾股定理得:(1+x)2=(4﹣x)2+32,
解之得:x=,
即CH=EH=,
∴在Rt△CHE中,由勾股定理得:CE=CH=.
10.解:(1)证明:∵AD平分∠BAC,
∴∠BAD=∠EAD,
∵AB=AE,AD=AD,
∴△ABD≌△AED(SAS),
∴DB=DE,∠BDA=∠EDA.
∵EF∥BC,
∴∠EFD=∠BDA,
∴∠EFD=∠EDF,
∴EF=ED,
∴EF=BD,
∵EF∥BD,
∴四边形BDEF为菱形.
(2)∵AD平分∠BAC,
∴∠BAC=2∠BAD,
∵AB=BC,
∴∠BAC=∠BCA=2∠BAD,
∵EF∥BC,
∴∠FEC=∠BCA=2∠BAD,
∵∠ABF=∠AEF,
∴∠ABF=2∠BAD.
所以图中度数等于∠BAD的2倍的所有的角:
∠BAC,∠BCA,∠ABF,∠AEF.
11.(1)解:∵四边形ABCD是菱形,
∴AC⊥BD,
∵E是AD的中点,
∴OE=AD=AE,
故答案为:=;
(2)证明:∵四边形ABCD是菱形,
∴OB=OD,
∵E是AD的中点,
∴OE是△ABD的中位线,
∴OE∥FG,
∵OG∥EF,
∴四边形OEFG是平行四边形,
∵EF⊥AB,
∴∠EFG=90°,
∴平行四边形OEFG是矩形;
(3)解:∵四边形ABCD是菱形,
∴BD⊥AC,AB=AD=10,
∴∠AOD=90°,
∵E是AD的中点,
∴OE=AE=AD=5;
由(1)知,四边形OEFG是矩形,
∴FG=OE=5,
∵AE=5,EF=4,
∴AF===3,
∴BG=AB﹣AF﹣FG=10﹣3﹣5=2.
12.解:(1)证明:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AFB=∠FBE,
∵BF平分∠ABC,
∴∠ABF=∠EBF,
∴∠AFB=∠ABF,
∴AF=AB,
∵AE⊥BF,
∴∠AOB=∠EOB=90°,
OB=OB,
∠ABO=∠EBO,
∴△ABO≌△EBO(ASA),
∴AB=BE,
∴AF=BE,
又AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=BE,
∴平行四边形ABEF是菱形.
(2)如图,作AG⊥BC于点G,
∵四边形ABEF是菱形,
OA=OE=AE=6,
OB=OF=BF=8,
∴AB==10,
BE=10,
设BG=x,则EG=BE﹣BG=10﹣x,
∴在Rt△ABG和Rt△AEG中,
根据勾股定理,得AG2=AB2﹣BG2=AE2﹣EG2
即102﹣x2=122﹣(10﹣x)2
解得x=,
∴AG==.
∴四边形ABCD的面积为:BC?AG=15×=144.
13.解:如图,过点D作DN⊥AB于N,DM⊥BC于F,
∵四边形ABCD是菱形,
∴AB=BC,
∵S菱形ABCD=AB×DN=BC×DM,
∴DN=DM,
∵∠BED+∠F=180°,∠BED+∠AED=180°,
∴∠F=∠AED,
又∵∠DNE=∠DMF,
∴△DNE≌△DMF(AAS)
∴DE=DF.
14.(1)证明:连接MN,如图1所示:
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠B=90°,
∴∠EAM=∠FCN,AC===5,
∵M,N分别是AD,BC的中点,
∴AM=DM=BN=CN,AM∥BN,
∴四边形ABNM是平行四边形,
又∵∠B=90°,
∴四边形ABNM是矩形,
∴MN=AB=3,
在△AME和△CNF中,,
∴△AME≌△CNF(SAS),
∴EM=FN,∠AEM=∠CFN,
∴∠MEF=∠NFE,
∴EM∥FN,
∴四边形EMFN是平行四边形,
又∵AE=CF=1,
∴EF=AC﹣AE﹣CF=3,
∴MN=EF,
∴四边形EMFN为矩形.
(2)解:连接MN,作MH⊥BC于H,如图2所示:
则四边形ABHM是矩形,
∴MH=AB=3,BH=AM=x,
∴HN=BC﹣BH﹣CN=4﹣2x,
∵四边形EMFN为矩形,AE=CF=0.5,
∴MN=EF=AC﹣AE﹣CF=4,
在Rt△MHN中,由勾股定理得:32+(4﹣2x)2=42,
∴x=2﹣.
15.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠OAF=∠OCE,
∵EF是线段AC的垂直平分线,
∴OA=OC,EF⊥AC,
在△AOF和△COE中,,
∴△AOF≌△COE(ASA),
∴AF=CE,
∴四边形AECF是平行四边形,
又∵EF⊥AC,
∴四边形AECF是菱形;
(2)解:由(1)得:四边形AECF是菱形,EF⊥AC,
∴CE=AE=2,OA=OC,OB=OD,
∵AC⊥AB,
∴EF∥AB,
∴∠OEC=∠B=30°,
∴OC=CE=1,OE=OC=,
∴AC=2OC=2,EF=2OE=2,
∴四边形AECF的面积=AC×EF=×2×2=2.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
