云南省蒙自高级中学2011-2012学年高二10月月考数学(文)试题
文档属性
| 名称 | 云南省蒙自高级中学2011-2012学年高二10月月考数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 193.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-02 19:04:09 | ||
图片预览


文档简介
一、选择题(本大题共12小题,每小题5分,满分60分.每小题4个选项中,只有1个选项符合题目要求)
1、集合A=,满足,则实数的取值范围是( )
A. B. C. D.
2、在2与16之间插入两个数、,使得成等比数列,则( )
A.4 B.8 C.16 D.32
3、已知函数,那么( )
A.当x∈(1,+∞)时,函数单调递增 B.当x∈(1,+∞)时,函数单调递减
C.当x∈(-∞,-1)时,函数单调递增 D.当x∈(-∞,3)时,函数单调递减
4、如图放置的几何体的俯视图为( )
5、已知向量,向量,若,则实数的值是( )
A.或 B.或 C.或 D.或
6、某学校共有老、中、青职工200人,其中有老年职工60人,中年职工人数与青年职工人数相等.现采用分层抽样的方法抽取部分职工进行调查,已知抽取的老年职工有12人,则抽取的青年职工应有( )
A.12人 B.14人 C.16人 D.20人
7、 在空间中,下列命题正确的是( )
A 平行于同一平面的两条直线平行 B 平行于同一直线的两个平面平行
C ( http: / / www. / wxc / ) 垂直于同一直线的两条直线平行 D 垂直于同一平面的两条直线平行
8、按右下图所表示的算法,若输入的是一个小于50的数,则输出的是( )
A.2005 B.65 C.64 D.63
9、 已知( )
(A) (B) (C) (D)
10、 若,则下列各式正确的是( )
A B
C ( http: / / www. / wxc / ) D
11、设,则函数的零点落在区间( )
A.(1,2) B.(2,3) C.(3,4) D. (4,5)
12、 一人连续投掷硬币两次,事件“至少有一次为正面”的互斥事件是( )
A.至多有一次为正面 B.两次均为正面
C.只有一次为正面 D.两次均为反面
二、填空题(本大题共4小题,每小题5分,满分20分)
13、 已知关于的不等式,它的解集是[ 1,3 ],则
实数的值是
14、函数的定义域是 。
15、长方体的三条侧棱长的比1:2:3,全面积是88,则长方体的体积是
16、设、满足约束条件,则的最大值是
三、解答题(本大题共6小题,第17题为10分,其余每题12分,共70分,解答题应写出文字说明及演算步骤.)
17.某市为了保障民生,防止居民住房价格过快增长,计划出台合理的房价调控政策,为此有关部门抽样调查了100个楼盘的住房销售价格,下表是这100个楼盘住房销售均价(单位:千元/平米)的频率分布表,根据下表回答以下问题:
(1)求下表中a,b的值;
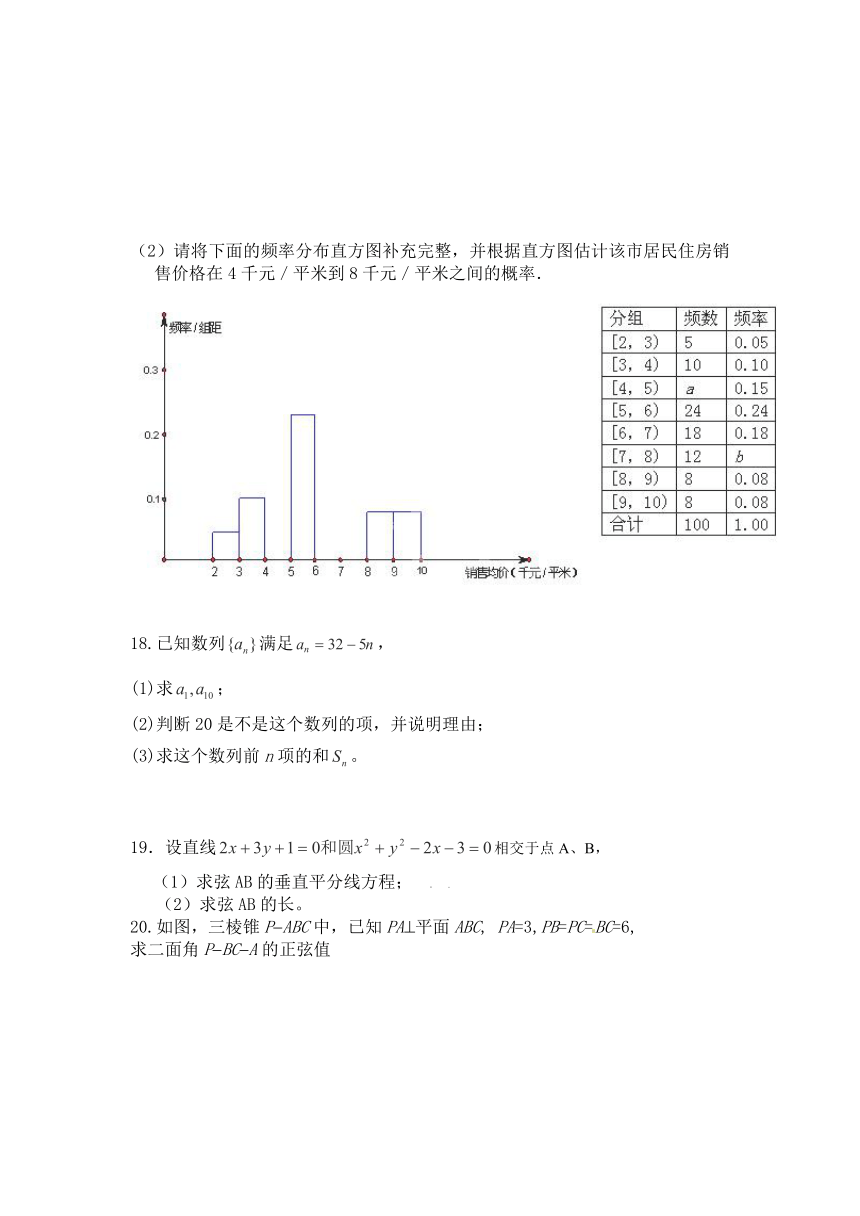
(2)请将下面的频率分布直方图补充完整,并根据直方图估计该市居民住房销售价格在4千元/平米到8千元/平米之间的概率.
18.已知数列满足,
(1)求;
(2)判断20是不是这个数列的项,并说明理由;
(3)求这个数列前n项的和。
19.设直线相交于点A、B,
(1)求弦AB的垂直平分线方程;
(2)求弦AB的长。
20.如图,三棱锥PABC中,已知PA平面ABC, PA=3,PB=PC=BC=6,
求二面角PBCA的正弦值
21 某单位计划建一长方体状的仓库, 底面如图, 高度为定值. 仓库的后墙和底部不花钱, 正面的造价为元, 两侧的造价为元, 顶部的造价为元. 设仓库正面的长为, 两侧的长各为.
(1)用表示这个仓库的总造价(元);
(2)若仓库底面面积时, 仓库的总造价最少是
多少元, 此时正面的长应设计为多少
22.已知:,
(1)求关于的表达式,并求的最小正周期;
(2)若时的最小值为5,求的值.
蒙自高级中学2011-2012学年高二10月考试卷答案
一、选择题
1~5 ADACC 6~10 BDDBA 11~12 AD
二、填空题
13、-2 14、x 15、48 16、5
三、解答题
解:(1)a=15 , b=0.12……………………………………… 4分
(2)率分布直方图如图 ……………………… 8分
该市居民住房销售价格在4千元/平米到8千元/平米之间的概率为0.69 … 10分
18.
(1)∵ ∴,。4分
(2)令=20得,这与矛盾,故20不是这个数列的项…… 8分
(3)由知,当时,
∴数列是公差为5的等差数列。故…………12分
19、解:(1)圆方程可整理为:,圆心坐标为(1,0),半径r=2,
易知弦AB的垂直平分线过圆心,且与直线AB垂直,
而
所以,由点斜式方程可得:
整理得:…………………6分
(2)圆心(1,0)到直线
故…………………12分
20、解:取BC的中点D,连结PD,AD,∵ PB =PC ,∴ PD⊥BC
∵ PA⊥平面ABC,由三垂线定理的逆定理得 AD⊥BC ( http: / / www. / wxc / )
∴ ∠PDA就是二面角P-BC-A的平面角 ………4分
∵ PB = PC = BC = 6 ,∴ PD =
sin∠PDA= 即二面角P-BC-A的正弦值是 ( http: / / www. / wxc / )
……………………………………………12分
21、解:⑴ 由题意得仓库的总造价为:
……………………………………… 4分
⑵ 仓库底面面积时,
…………………… 8分
当且仅当时, 等号成立, … 10分
又∵ , ∴ .……………………12分
22、解:(1)
.
∴的最小正周期是.
(2) ∵,
∴,
∴当,即时,函数 取得最小值是.
∵,
∴
开始
输入
计算的值
2004
使的值增加1
N
输出
Y
结束
1、集合A=,满足,则实数的取值范围是( )
A. B. C. D.
2、在2与16之间插入两个数、,使得成等比数列,则( )
A.4 B.8 C.16 D.32
3、已知函数,那么( )
A.当x∈(1,+∞)时,函数单调递增 B.当x∈(1,+∞)时,函数单调递减
C.当x∈(-∞,-1)时,函数单调递增 D.当x∈(-∞,3)时,函数单调递减
4、如图放置的几何体的俯视图为( )
5、已知向量,向量,若,则实数的值是( )
A.或 B.或 C.或 D.或
6、某学校共有老、中、青职工200人,其中有老年职工60人,中年职工人数与青年职工人数相等.现采用分层抽样的方法抽取部分职工进行调查,已知抽取的老年职工有12人,则抽取的青年职工应有( )
A.12人 B.14人 C.16人 D.20人
7、 在空间中,下列命题正确的是( )
A 平行于同一平面的两条直线平行 B 平行于同一直线的两个平面平行
C ( http: / / www. / wxc / ) 垂直于同一直线的两条直线平行 D 垂直于同一平面的两条直线平行
8、按右下图所表示的算法,若输入的是一个小于50的数,则输出的是( )
A.2005 B.65 C.64 D.63
9、 已知( )
(A) (B) (C) (D)
10、 若,则下列各式正确的是( )
A B
C ( http: / / www. / wxc / ) D
11、设,则函数的零点落在区间( )
A.(1,2) B.(2,3) C.(3,4) D. (4,5)
12、 一人连续投掷硬币两次,事件“至少有一次为正面”的互斥事件是( )
A.至多有一次为正面 B.两次均为正面
C.只有一次为正面 D.两次均为反面
二、填空题(本大题共4小题,每小题5分,满分20分)
13、 已知关于的不等式,它的解集是[ 1,3 ],则
实数的值是
14、函数的定义域是 。
15、长方体的三条侧棱长的比1:2:3,全面积是88,则长方体的体积是
16、设、满足约束条件,则的最大值是
三、解答题(本大题共6小题,第17题为10分,其余每题12分,共70分,解答题应写出文字说明及演算步骤.)
17.某市为了保障民生,防止居民住房价格过快增长,计划出台合理的房价调控政策,为此有关部门抽样调查了100个楼盘的住房销售价格,下表是这100个楼盘住房销售均价(单位:千元/平米)的频率分布表,根据下表回答以下问题:
(1)求下表中a,b的值;
(2)请将下面的频率分布直方图补充完整,并根据直方图估计该市居民住房销售价格在4千元/平米到8千元/平米之间的概率.
18.已知数列满足,
(1)求;
(2)判断20是不是这个数列的项,并说明理由;
(3)求这个数列前n项的和。
19.设直线相交于点A、B,
(1)求弦AB的垂直平分线方程;
(2)求弦AB的长。
20.如图,三棱锥PABC中,已知PA平面ABC, PA=3,PB=PC=BC=6,
求二面角PBCA的正弦值
21 某单位计划建一长方体状的仓库, 底面如图, 高度为定值. 仓库的后墙和底部不花钱, 正面的造价为元, 两侧的造价为元, 顶部的造价为元. 设仓库正面的长为, 两侧的长各为.
(1)用表示这个仓库的总造价(元);
(2)若仓库底面面积时, 仓库的总造价最少是
多少元, 此时正面的长应设计为多少
22.已知:,
(1)求关于的表达式,并求的最小正周期;
(2)若时的最小值为5,求的值.
蒙自高级中学2011-2012学年高二10月考试卷答案
一、选择题
1~5 ADACC 6~10 BDDBA 11~12 AD
二、填空题
13、-2 14、x 15、48 16、5
三、解答题
解:(1)a=15 , b=0.12……………………………………… 4分
(2)率分布直方图如图 ……………………… 8分
该市居民住房销售价格在4千元/平米到8千元/平米之间的概率为0.69 … 10分
18.
(1)∵ ∴,。4分
(2)令=20得,这与矛盾,故20不是这个数列的项…… 8分
(3)由知,当时,
∴数列是公差为5的等差数列。故…………12分
19、解:(1)圆方程可整理为:,圆心坐标为(1,0),半径r=2,
易知弦AB的垂直平分线过圆心,且与直线AB垂直,
而
所以,由点斜式方程可得:
整理得:…………………6分
(2)圆心(1,0)到直线
故…………………12分
20、解:取BC的中点D,连结PD,AD,∵ PB =PC ,∴ PD⊥BC
∵ PA⊥平面ABC,由三垂线定理的逆定理得 AD⊥BC ( http: / / www. / wxc / )
∴ ∠PDA就是二面角P-BC-A的平面角 ………4分
∵ PB = PC = BC = 6 ,∴ PD =
sin∠PDA= 即二面角P-BC-A的正弦值是 ( http: / / www. / wxc / )
……………………………………………12分
21、解:⑴ 由题意得仓库的总造价为:
……………………………………… 4分
⑵ 仓库底面面积时,
…………………… 8分
当且仅当时, 等号成立, … 10分
又∵ , ∴ .……………………12分
22、解:(1)
.
∴的最小正周期是.
(2) ∵,
∴,
∴当,即时,函数 取得最小值是.
∵,
∴
开始
输入
计算的值
2004
使的值增加1
N
输出
Y
结束
同课章节目录
