小学数学冀教版五年级下 8.1用集合图表示问题 课件(18页ppt)
文档属性
| 名称 | 小学数学冀教版五年级下 8.1用集合图表示问题 课件(18页ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-24 17:56:28 | ||
图片预览





文档简介
冀教版五年级数学下册
简单的集合问题
两个爸爸和两个儿子一同去看电影,他们只买了3张票,却顺利通过检验进入了电影院。这是为神马?
6+6-1=11(人)
答:共有11人。
排队问题:
从前面数,从后面数,丽丽都排第6,这一排共有几个人?
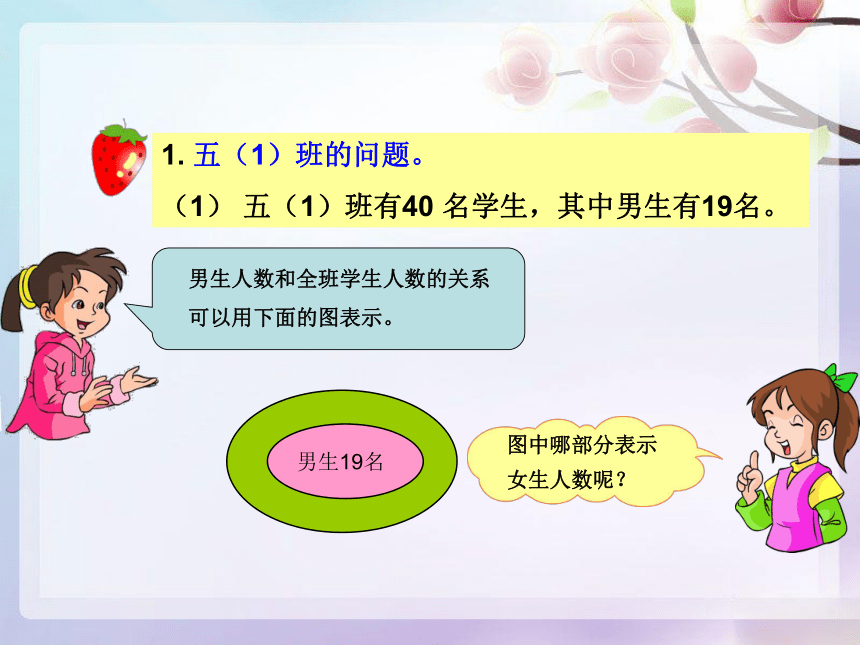
1. 五(1)班的问题。
(1) 五(1)班有40 名学生,其中男生有19名。
男生人数和全班学生人数的关系
可以用下面的图表示。
男生19名
图中哪部分表示
女生人数呢?
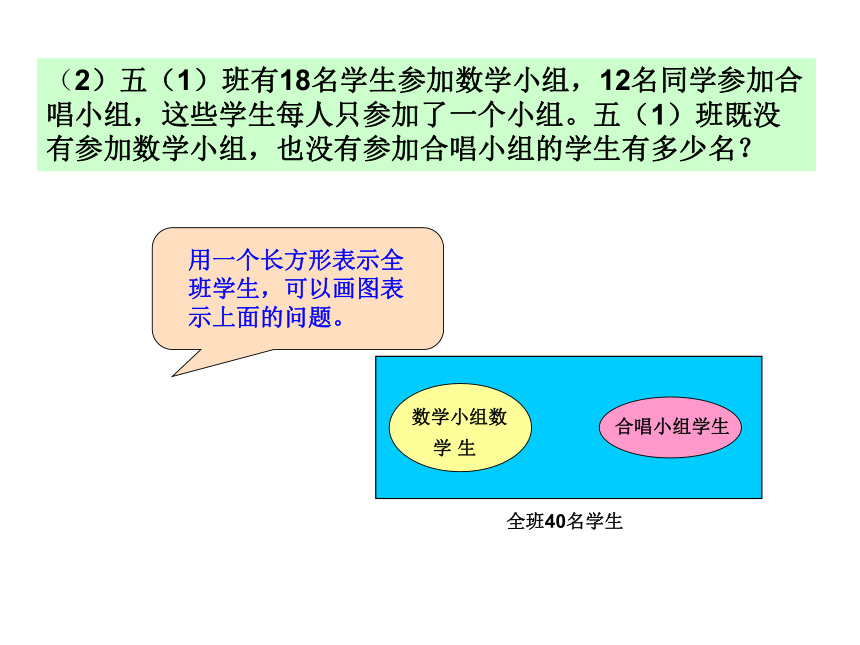
(2)五(1)班有18名学生参加数学小组,12名同学参加合唱小组,这些学生每人只参加了一个小组。五(1)班既没有参加数学小组,也没有参加合唱小组的学生有多少名?
用一个长方形表示全班学生,可以画图表示上面的问题。
合唱小组学生
数学小组数
学 生
全班40名学生
练一练:
你能用集合图表示下面两者之间的关系吗?
1.无限小数和循环小数
2.真分数和分数
3.方程和等式
合唱小组学生
数学小组数
学 生
全班40名学生
图中蓝色部分表示
哪部分学生?
既没有参加数学
小组,也没有参加合唱小
组……
列出算式计算:
40﹣18﹣12=10(名)
(3)在学校春季运动会上,五(1)班学生参加了两项比赛。有18名学生参加田径比赛,10名学生参加篮球比赛,其中有8名学生既参加了田径比赛又参加了篮球比赛。五(1)班共有多少名学生参加比赛?
参加田径比
赛的学生
参加篮球比
赛的学生
田径和篮球比赛都参加的学生
因为把参加两项比赛的人数相加,有8名学生是算了两次……
你能解释为什么减去8吗?
五(1)班参加比赛的学生共有:
18+10-8=20(名)
“至少有一门得满分”就是说只有语文一门得
满分的、只有数学一门的满分的、语数双百
的同学都是要求的人数。
一次期末考试,某班有15人数学得满分,有12人语文得满分,并且有4人语、数都是满分,那么这个班至少有一门得满分的同学有多少人?
我们可以画图来帮助理解。
解题过程:
15+12-4=23(人)
答:这个班至少有一门得满分的同学有23人。
容斥原理:(1)如果被计数的事物有A、B两类,
那么,A类或B类元素个数 = A类元素个数 + B类元
素个数 - 既是A类又是B类的元素个数。
A
B
五年级学生参加语文、数学考试,每人至少有一门功课取得优秀成绩。其中语文成绩优秀的有65人,数学优秀的有87人。语文、数学都优秀的有30人,问五年级一共有多少人?
语文优秀的人数:65人
数学优秀的人数:87人
两科都优秀的人数30人
?人
65+87-30=122(人)
答:五年级一共有122人。
五年级96名学生都订了刊物,有64人订了少年报,有48人订了小学生报,问两种刊物都订的有多少人?
64人
48人
?人(两种都订的)
96人
64+48-96=112-96=16(人)
1、全班46名同学,仅会打乒乓球的有28人,会打乒乓球又会打羽毛球的有10人,不会打乒乓球又不会打羽毛球的有6人,仅会打羽毛球的有多少人?
挑战
一班有45人,其中26人参加了数学竞赛,22人参加了作文比赛,12人两项比赛都参加了。一班有多少人两项比赛都没有参加?
解题过程:
26+22-12=36(人) 45-36=9(人)
答:那么这个班一共有82人两项比赛都没有参加。
小知识:
?容斥问题
容—包括
斥—排除
容斥原理:先不考虑重叠的情况,把包含于某内容中的
所有对象的数目先计算出来,然后再把计算
时重复计算的数目排斥出去,使得计算的结
果既无遗漏又无重复。
挑战
东方小学五(1)班许多学生参加了学习小组。已知参加语文学习小组的有35人,参加数学小组的有32人,参加英语小组的有45人,同学同时参加语文和和数学的有10人,同时参加语文和英语小组的有12人,同时参加数学和英语的有15人,三个学习小组都参加的有5人。问那么五(1)班一共有多少人参加了学习小组?
解题过程:
35+32+45-10-12-15+5=82(人)
答:那么这个班一共有82人参加了学习小组。
语文
数学
英语
容斥原理:(2)如果被计数的事物有A、B、C三类,
那么,A类或B类或C类元素个数=A类元素个数+B类
元素个数+C类元素个数—既是A类又是B类的元素个
数—既是A类又是C类的元素个数—既是B类又是C类
的元素个数+既是A类又是B类而且是C类的元素个数。
A
B
C
简单的集合问题
两个爸爸和两个儿子一同去看电影,他们只买了3张票,却顺利通过检验进入了电影院。这是为神马?
6+6-1=11(人)
答:共有11人。
排队问题:
从前面数,从后面数,丽丽都排第6,这一排共有几个人?
1. 五(1)班的问题。
(1) 五(1)班有40 名学生,其中男生有19名。
男生人数和全班学生人数的关系
可以用下面的图表示。
男生19名
图中哪部分表示
女生人数呢?
(2)五(1)班有18名学生参加数学小组,12名同学参加合唱小组,这些学生每人只参加了一个小组。五(1)班既没有参加数学小组,也没有参加合唱小组的学生有多少名?
用一个长方形表示全班学生,可以画图表示上面的问题。
合唱小组学生
数学小组数
学 生
全班40名学生
练一练:
你能用集合图表示下面两者之间的关系吗?
1.无限小数和循环小数
2.真分数和分数
3.方程和等式
合唱小组学生
数学小组数
学 生
全班40名学生
图中蓝色部分表示
哪部分学生?
既没有参加数学
小组,也没有参加合唱小
组……
列出算式计算:
40﹣18﹣12=10(名)
(3)在学校春季运动会上,五(1)班学生参加了两项比赛。有18名学生参加田径比赛,10名学生参加篮球比赛,其中有8名学生既参加了田径比赛又参加了篮球比赛。五(1)班共有多少名学生参加比赛?
参加田径比
赛的学生
参加篮球比
赛的学生
田径和篮球比赛都参加的学生
因为把参加两项比赛的人数相加,有8名学生是算了两次……
你能解释为什么减去8吗?
五(1)班参加比赛的学生共有:
18+10-8=20(名)
“至少有一门得满分”就是说只有语文一门得
满分的、只有数学一门的满分的、语数双百
的同学都是要求的人数。
一次期末考试,某班有15人数学得满分,有12人语文得满分,并且有4人语、数都是满分,那么这个班至少有一门得满分的同学有多少人?
我们可以画图来帮助理解。
解题过程:
15+12-4=23(人)
答:这个班至少有一门得满分的同学有23人。
容斥原理:(1)如果被计数的事物有A、B两类,
那么,A类或B类元素个数 = A类元素个数 + B类元
素个数 - 既是A类又是B类的元素个数。
A
B
五年级学生参加语文、数学考试,每人至少有一门功课取得优秀成绩。其中语文成绩优秀的有65人,数学优秀的有87人。语文、数学都优秀的有30人,问五年级一共有多少人?
语文优秀的人数:65人
数学优秀的人数:87人
两科都优秀的人数30人
?人
65+87-30=122(人)
答:五年级一共有122人。
五年级96名学生都订了刊物,有64人订了少年报,有48人订了小学生报,问两种刊物都订的有多少人?
64人
48人
?人(两种都订的)
96人
64+48-96=112-96=16(人)
1、全班46名同学,仅会打乒乓球的有28人,会打乒乓球又会打羽毛球的有10人,不会打乒乓球又不会打羽毛球的有6人,仅会打羽毛球的有多少人?
挑战
一班有45人,其中26人参加了数学竞赛,22人参加了作文比赛,12人两项比赛都参加了。一班有多少人两项比赛都没有参加?
解题过程:
26+22-12=36(人) 45-36=9(人)
答:那么这个班一共有82人两项比赛都没有参加。
小知识:
?容斥问题
容—包括
斥—排除
容斥原理:先不考虑重叠的情况,把包含于某内容中的
所有对象的数目先计算出来,然后再把计算
时重复计算的数目排斥出去,使得计算的结
果既无遗漏又无重复。
挑战
东方小学五(1)班许多学生参加了学习小组。已知参加语文学习小组的有35人,参加数学小组的有32人,参加英语小组的有45人,同学同时参加语文和和数学的有10人,同时参加语文和英语小组的有12人,同时参加数学和英语的有15人,三个学习小组都参加的有5人。问那么五(1)班一共有多少人参加了学习小组?
解题过程:
35+32+45-10-12-15+5=82(人)
答:那么这个班一共有82人参加了学习小组。
语文
数学
英语
容斥原理:(2)如果被计数的事物有A、B、C三类,
那么,A类或B类或C类元素个数=A类元素个数+B类
元素个数+C类元素个数—既是A类又是B类的元素个
数—既是A类又是C类的元素个数—既是B类又是C类
的元素个数+既是A类又是B类而且是C类的元素个数。
A
B
C
