第11课时 矩形与菱形的综合练习(共18张ppt)
文档属性
| 名称 | 第11课时 矩形与菱形的综合练习(共18张ppt) |
|
|
| 格式 | ppt | ||
| 文件大小 | 802.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-24 21:06:57 | ||
图片预览



文档简介
有一个角是直角的平行四边形是矩形。
考考你
对角线相等的四边形是矩形。
对角线互相平分且相等的四边形是矩形。
有一个角是直角的四边形是矩形。
四个角都是直角的四边形是矩形。
四个角都相等的四边形是矩形。
对角线相等且有一个角是直角的四边形是矩形。
对角线相等且互相垂直的四边形是矩形。
1、如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E,四边形CEDO是矩形吗?说出你的理由.
矩形与菱形的综合练行四边形有哪些性质?
平行四
边形
对称性
对角线
角
边
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
矩形和菱形的性质:
1、具有平行四边形的一切性质
2、菱形的四条边都相等
3、菱形的对角线互相垂直,并且每一条对角线平分一组对角
1、具有平行四边形的一切性质
2、四个角都是直角
3、矩形的对角线相等
性
质
有一组邻边相等的平行四边形
有一个角是直角的平行四边形
定义
菱形
矩形
定义
有三个角是直角的四边形是矩形。
矩形判定定理1
对角线相等的平行四边形是矩形。
矩形判定定理2
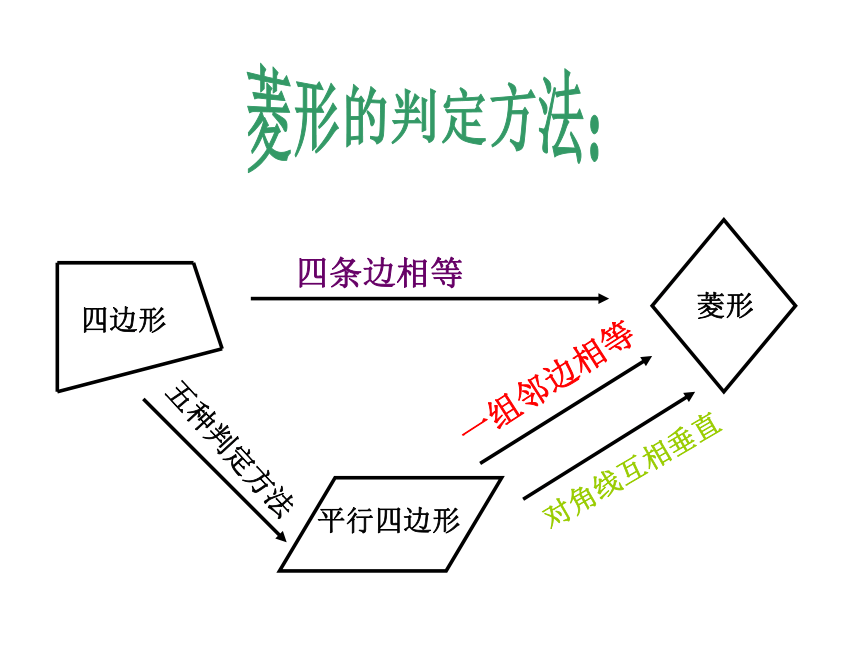
一组邻边相等
对角线互相垂直
四条边相等
五种判定方法
四边形
平行四边形
菱形
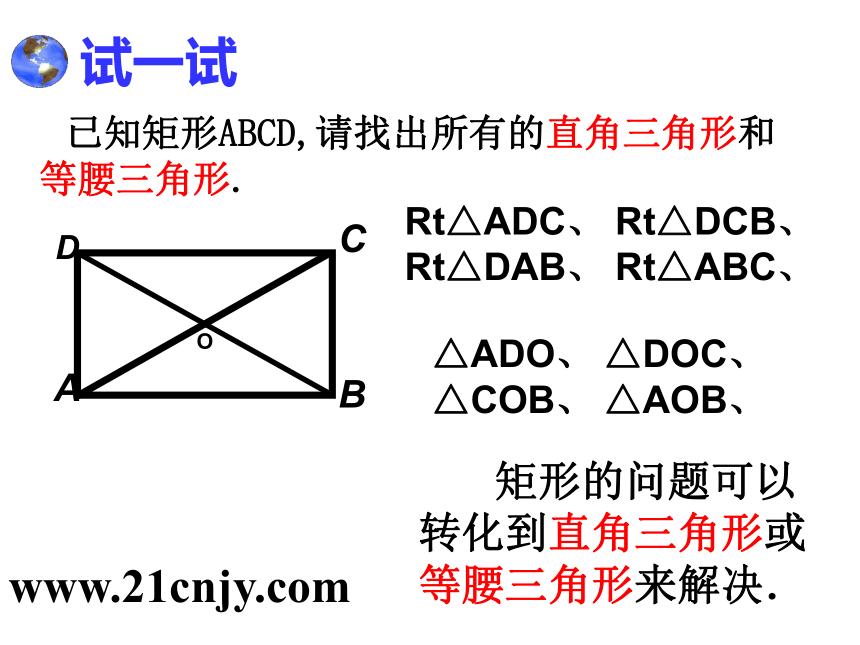
试一试
已知矩形ABCD,请找出所有的直角三角形和等腰三角形.
A
B
C
D
O
矩形的问题可以转化到直角三角形或等腰三角形来解决.
Rt△ADC、
Rt△DCB、
Rt△DAB、
Rt△ABC、
△ADO、
△DOC、
△COB、
△AOB、
www.21cnjy.com
相等的线段:
相等的角:
等腰三角形:
直角三角形:
全等三角形:
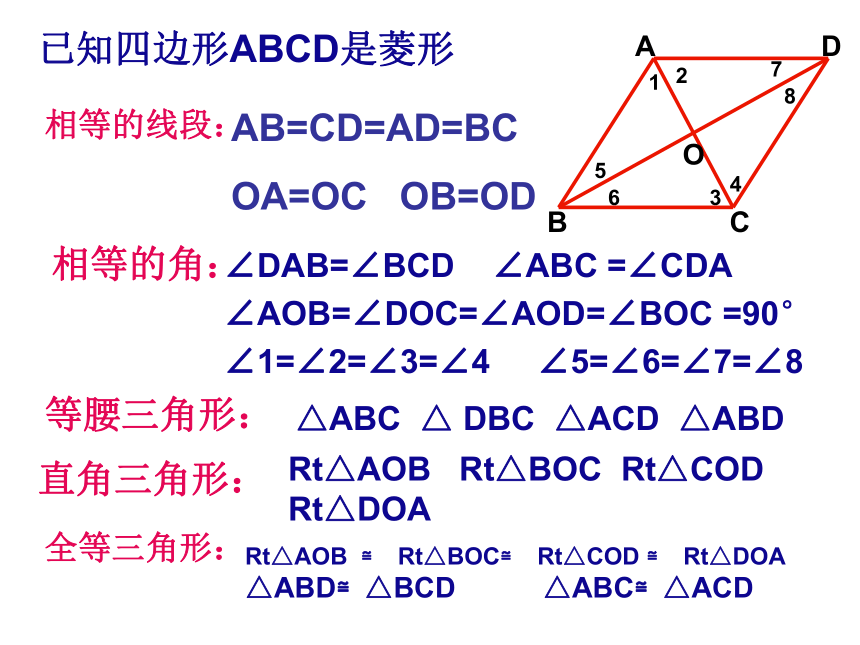
已知四边形ABCD是菱形
AB=CD=AD=BC
OA=OC
OB=OD
∠DAB=∠BCD
∠ABC
=∠CDA
∠AOB=∠DOC=∠AOD=∠BOC
=90°
∠1=∠2=∠3=∠4
∠5=∠6=∠7=∠8
△ABC
△
DBC
△ACD
△ABD
Rt△AOB
Rt△BOC
Rt△COD
Rt△DOA
Rt△AOB
≌
Rt△BOC≌
Rt△COD
≌
Rt△DOA
△ABD≌△BCD
△ABC≌△ACD
A
B
C
D
O
1
2
3
4
5
6
7
8
1.对角线相等且一组对边也相等的四边
形是矩形.
2.两条对角线交点到四个顶点距离相等的四边形为矩形.
3.有一组对边相等,一组对角是直角的四边形是矩形.
4.有三个角都相等的四边形是矩形.
判断题
×
√
√
×
巩固新知
5.
具备条件____的四边形是矩形.
A.两条对角线相等
B.对角线互相垂直
C.一组对角是直角
D.有三个角是直角
6.
能够判断一个四边形是矩形的条件是
A.对角线相等
B.对角线垂直
C.对角线互相平分且相等
D.对角线垂直且相等
选择题
C
D
巩固新知
判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.
√
╳
╳
╳
□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是
形;
(2)若AC=BD,则□ABCD是
形;
(3)若∠ABC是直角,则□ABCD是
形;
(4)若∠BAO=∠DAO,则□ABCD是
形。
A
B
C
D
O
菱
矩
矩
菱
作
业
19
四边形
补充题
第十九章
四边形
2.已知:如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD,PD、PC相交于点P。
(1)猜想:四边形PCOD是什么特殊的四边形?
(2)试证明你的猜想。
(3)?
PO与CD有怎样的关系?
四边形PCOD是菱形。
PO与CD互相垂直且平分
△ABC中,点O是AC边上一动点,过O点作直线MN//BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,
(1)试说明EO=OF的理由。
(2)当点O运动到何处时,四边形AECF是矩形?并说明你的结论。
M
N
B
C
D
E
O
F
A
(3)在⑵的条件下,当AC与BC满足什么条件时四边形AECF是正方形?并说明你的结论。
思考:已知:菱形中ABCD,∠A=72°,请设计三种不同的分法,将菱形ABCD分成四个三角形,使得每一个三角形都是等腰三角形。
如图,△ABC为直角三角形,∠C=90°,现将补成矩形,使△ABC的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,那么符合要求的矩形可以画出两个,矩形ACBD和矩形AEFB
1)矩形ACBD和矩形AEFB的
面积有何数量关系?
2)如果△ABC是钝角三角形,
按短文中的要求把它补成矩形那么
符合要求的矩形可以画出几个?
试试看。
3)如果△ABC是锐角三角形呢?
A
C
B
F
E
D
考考你
对角线相等的四边形是矩形。
对角线互相平分且相等的四边形是矩形。
有一个角是直角的四边形是矩形。
四个角都是直角的四边形是矩形。
四个角都相等的四边形是矩形。
对角线相等且有一个角是直角的四边形是矩形。
对角线相等且互相垂直的四边形是矩形。
1、如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E,四边形CEDO是矩形吗?说出你的理由.
矩形与菱形的综合练行四边形有哪些性质?
平行四
边形
对称性
对角线
角
边
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
矩形和菱形的性质:
1、具有平行四边形的一切性质
2、菱形的四条边都相等
3、菱形的对角线互相垂直,并且每一条对角线平分一组对角
1、具有平行四边形的一切性质
2、四个角都是直角
3、矩形的对角线相等
性
质
有一组邻边相等的平行四边形
有一个角是直角的平行四边形
定义
菱形
矩形
定义
有三个角是直角的四边形是矩形。
矩形判定定理1
对角线相等的平行四边形是矩形。
矩形判定定理2
一组邻边相等
对角线互相垂直
四条边相等
五种判定方法
四边形
平行四边形
菱形
试一试
已知矩形ABCD,请找出所有的直角三角形和等腰三角形.
A
B
C
D
O
矩形的问题可以转化到直角三角形或等腰三角形来解决.
Rt△ADC、
Rt△DCB、
Rt△DAB、
Rt△ABC、
△ADO、
△DOC、
△COB、
△AOB、
www.21cnjy.com
相等的线段:
相等的角:
等腰三角形:
直角三角形:
全等三角形:
已知四边形ABCD是菱形
AB=CD=AD=BC
OA=OC
OB=OD
∠DAB=∠BCD
∠ABC
=∠CDA
∠AOB=∠DOC=∠AOD=∠BOC
=90°
∠1=∠2=∠3=∠4
∠5=∠6=∠7=∠8
△ABC
△
DBC
△ACD
△ABD
Rt△AOB
Rt△BOC
Rt△COD
Rt△DOA
Rt△AOB
≌
Rt△BOC≌
Rt△COD
≌
Rt△DOA
△ABD≌△BCD
△ABC≌△ACD
A
B
C
D
O
1
2
3
4
5
6
7
8
1.对角线相等且一组对边也相等的四边
形是矩形.
2.两条对角线交点到四个顶点距离相等的四边形为矩形.
3.有一组对边相等,一组对角是直角的四边形是矩形.
4.有三个角都相等的四边形是矩形.
判断题
×
√
√
×
巩固新知
5.
具备条件____的四边形是矩形.
A.两条对角线相等
B.对角线互相垂直
C.一组对角是直角
D.有三个角是直角
6.
能够判断一个四边形是矩形的条件是
A.对角线相等
B.对角线垂直
C.对角线互相平分且相等
D.对角线垂直且相等
选择题
C
D
巩固新知
判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.
√
╳
╳
╳
□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是
形;
(2)若AC=BD,则□ABCD是
形;
(3)若∠ABC是直角,则□ABCD是
形;
(4)若∠BAO=∠DAO,则□ABCD是
形。
A
B
C
D
O
菱
矩
矩
菱
作
业
19
四边形
补充题
第十九章
四边形
2.已知:如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD,PD、PC相交于点P。
(1)猜想:四边形PCOD是什么特殊的四边形?
(2)试证明你的猜想。
(3)?
PO与CD有怎样的关系?
四边形PCOD是菱形。
PO与CD互相垂直且平分
△ABC中,点O是AC边上一动点,过O点作直线MN//BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,
(1)试说明EO=OF的理由。
(2)当点O运动到何处时,四边形AECF是矩形?并说明你的结论。
M
N
B
C
D
E
O
F
A
(3)在⑵的条件下,当AC与BC满足什么条件时四边形AECF是正方形?并说明你的结论。
思考:已知:菱形中ABCD,∠A=72°,请设计三种不同的分法,将菱形ABCD分成四个三角形,使得每一个三角形都是等腰三角形。
如图,△ABC为直角三角形,∠C=90°,现将补成矩形,使△ABC的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,那么符合要求的矩形可以画出两个,矩形ACBD和矩形AEFB
1)矩形ACBD和矩形AEFB的
面积有何数量关系?
2)如果△ABC是钝角三角形,
按短文中的要求把它补成矩形那么
符合要求的矩形可以画出几个?
试试看。
3)如果△ABC是锐角三角形呢?
A
C
B
F
E
D
