第14课时 正方形的定义和性质(共34张ppt)
文档属性
| 名称 | 第14课时 正方形的定义和性质(共34张ppt) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-24 00:00:00 | ||
图片预览



文档简介
5、如图正方形ABCD中,点F是BC边上一点,延长AB到E使BE=BF,连接CE,连接AF并延长交CE于点G. 请你判断AG与CE有何关系并说明理由.
满足下列条件的四边形是不是正方形:
1、对角线互相垂直且相等的平行四 边形;
2、对角线互相垂直的矩形;
3、对角线相等的菱形;
4、对角线互相垂直平分且相等的四 边形。
正方形的定义和性质
正方形
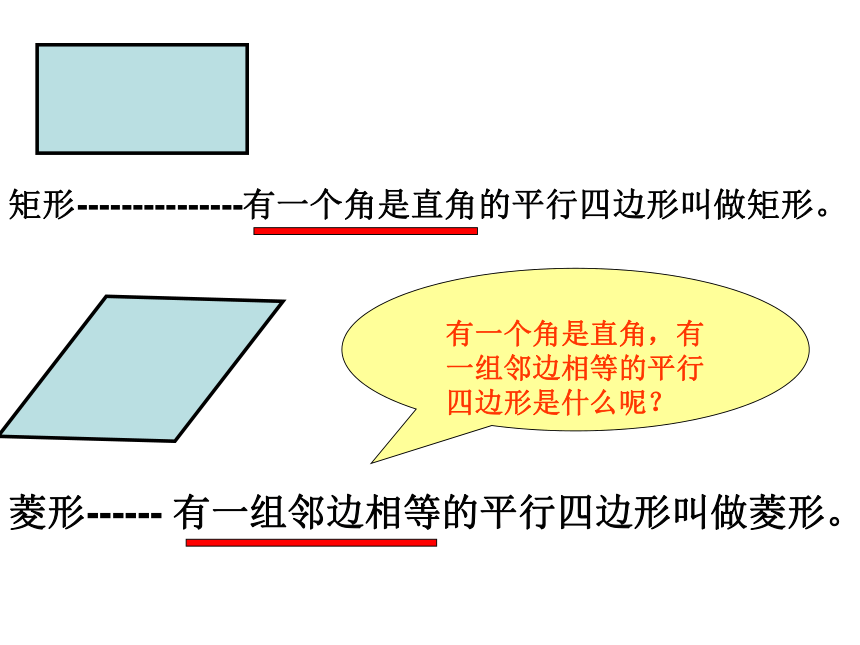
矩形---------------有一个角是直角的平行四边形叫做矩形。
菱形------ 有一组邻边相等的平行四边形叫做菱形。
有一个角是直角,有一组邻边相等的平行四边形是什么呢?
矩 形
〃
〃
正方形
邻边
相等
〃
〃
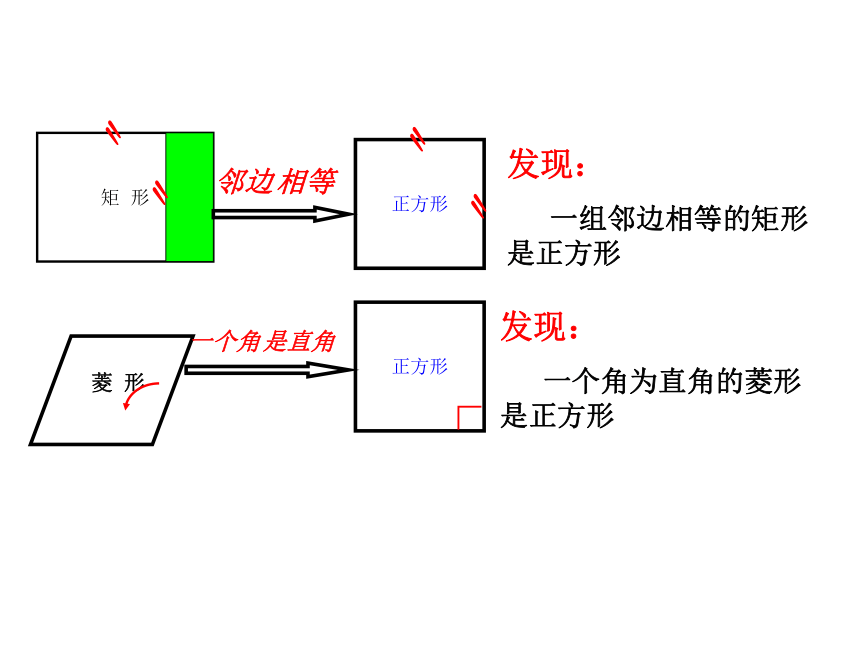
发现:
一组邻边相等的矩形 是正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
有一个直角
一组邻边相等
一组邻边相等
有一个直角
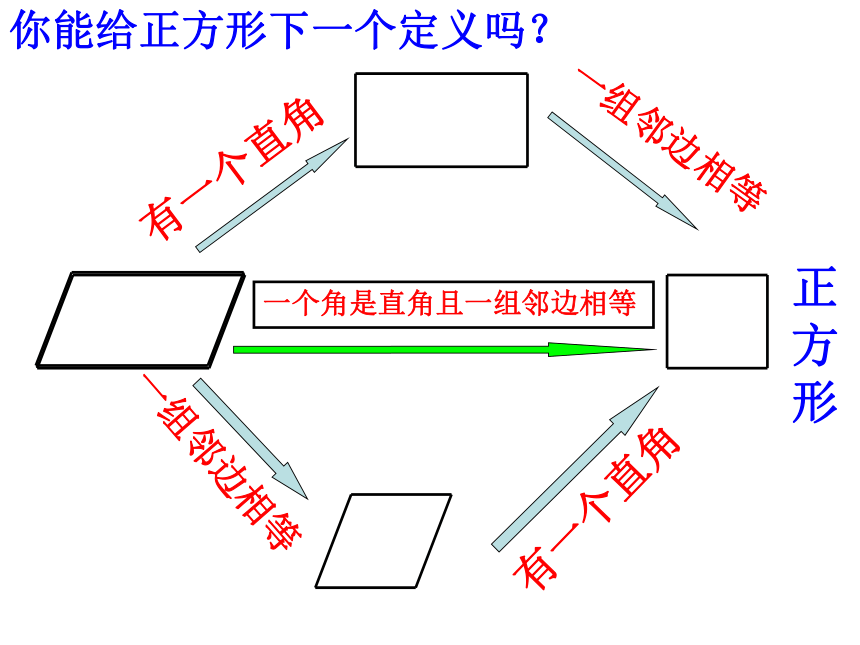
你能给正方形下一个定义吗?
一个角是直角且一组邻边相等
正方形
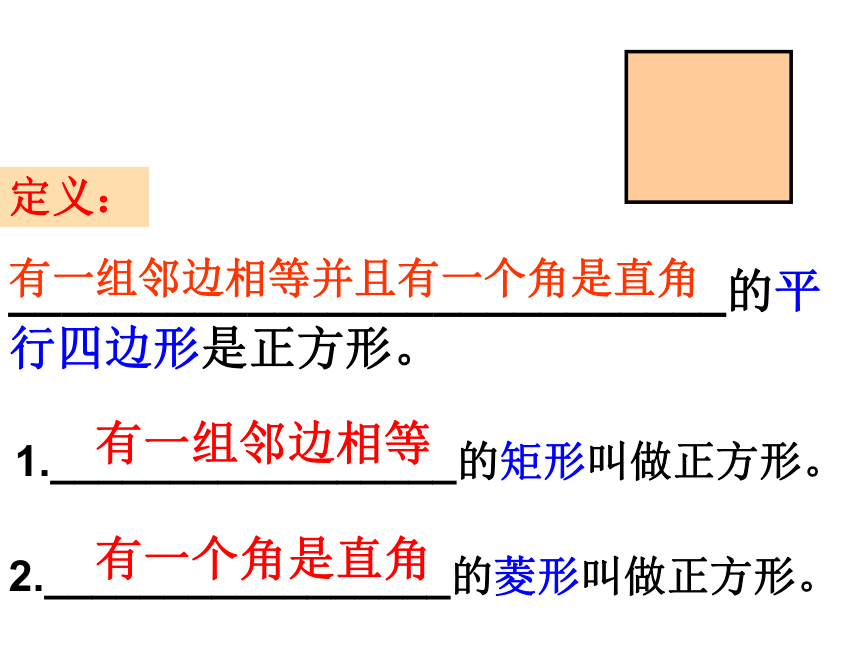
1._________________的矩形叫做正方形。
有一组邻边相等
2._________________的菱形叫做正方形。
有一个角是直角
有一组邻边相等并且有一个角是直角
___________________________的平行四边形是正方形。
定义:
四边形
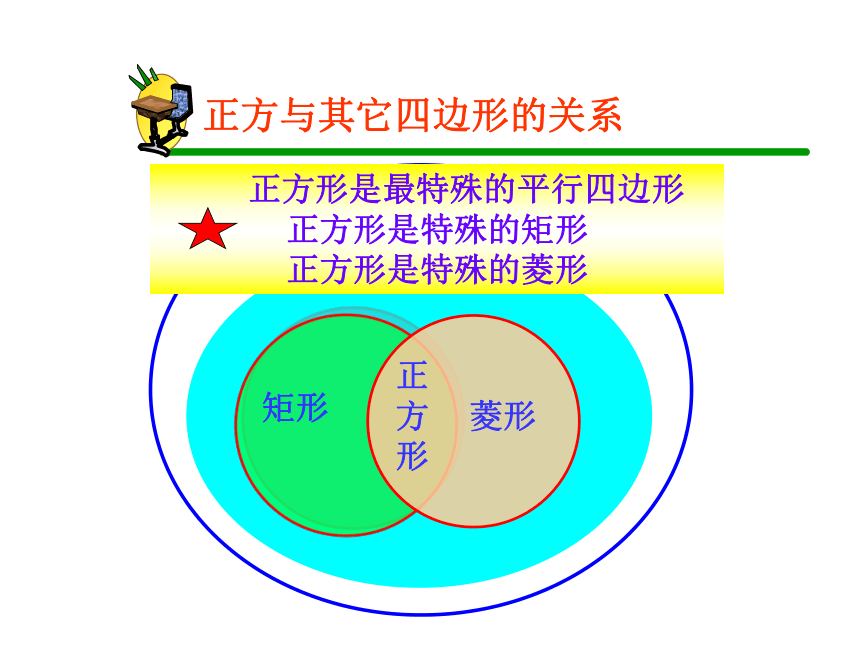
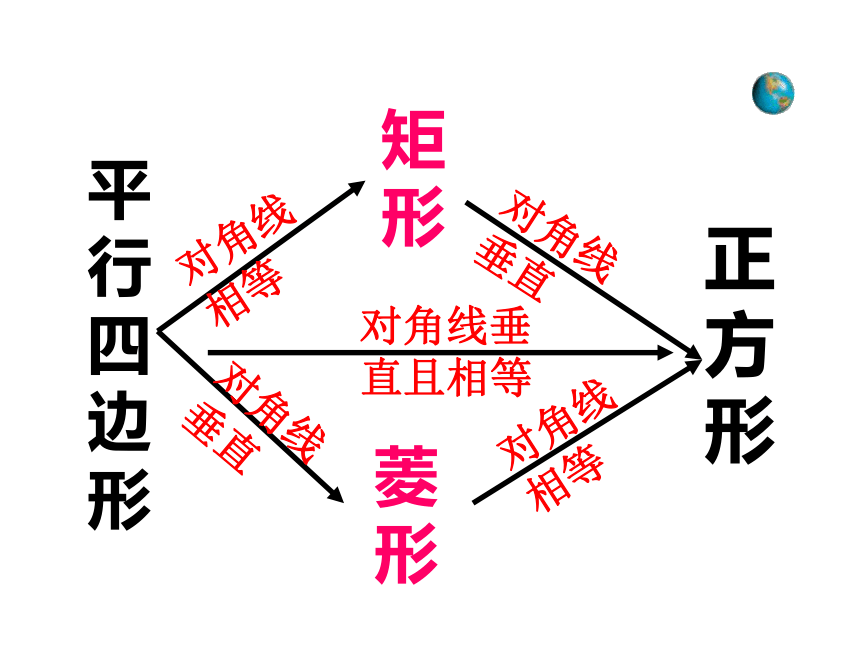
正方与其它四边形的关系
平行四边形
矩形
菱形
正方形
正方形是最特殊的平行四边形
正方形是特殊的矩形
正方形是特殊的菱形
平行四边形
矩形
菱形
正方形
第十九章 四边形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
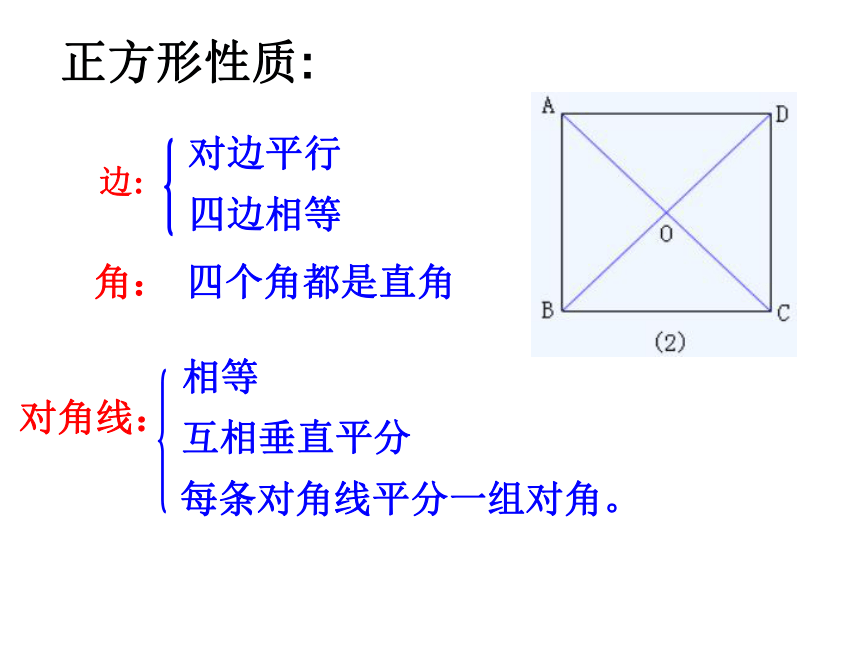
正方形的性质=
边:
每条对角线平分一组对角。
对边平行
四边相等
四个角都是直角
正方形性质:
角:
对角线:
相等
互相垂直平分
平行四边形
矩形
菱形
正方形
对角线相等
对角线垂直
对角线相等
对角线垂直
对角线垂直且相等
第十九章 四边形
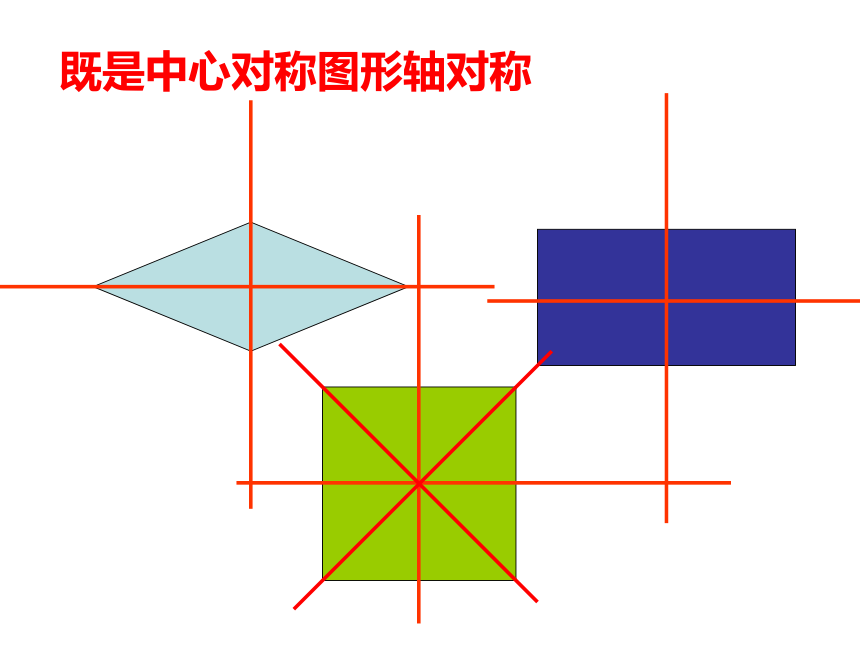
既是中心对称图形轴对称
第十九章 四边形
第十九章 四边形
下列说法对吗?
(1)四个角都相等的四边形是正方形
(2)四条边都相等的四边形是正方形
(3)四边相等,有一角是直角的四边形是正方形
(4) 正方形的一条对角线把正方形分成两个全等的等腰 直角三角形
(5) 正方形是轴对称图形,一共有2条对称轴
正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直.
C、对角互补.
D、对角线相等.
2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直.
C、对角线平分一组对角.
D、对角线相等.
B
D
随堂练习
1. 下列说法是否正确,并说明理由.
①对角线相等的菱形是正方形( )
②对角线互相垂直的矩形是正方形( )
③对角线垂直且相等的平行四边形是正方形( )
④四条边都相等的四边形是正方形( )
⑤四个角相等的四边形是正方形( )
√
√
√
×
×
2. 正方形的四条边______,四个角_______,两条对角线______________________ .
相等
相等
相等且互相垂直平分
判断下列说法是对还是错:
正方形的一条对角线把正方形
分成两个全等的等腰直角三角形。
对
两条对角线呢?
判断下列说法是对还是错:
如果一个矩形的对角线互相垂直,那么它一定是正方形。
对
判断下列说法是对还是错:
如果一个菱形的对角线相等,那么它一定是正方形。
对
判断下列说法是对还是错:
四条边相等,且有一个角是直角的四边形是正方形。
对
四边形再认识
第十九章 四边形
A
B
C
D
O
(2)若AC=4,则正方形边长 ; 正方形的面积是
四边形ABCD是正方形,两条对角线相交于点O,(1)求∠AOB,∠OAB的度数。
8
解:
(1)∵四边形ABCD是正方形
∴AC⊥BD ∠AOB=900
∠BAC=∠DAC
∴∠OAB=450
A
B
C
D
O
E
4㎝
(3)正方形的面积64cm,则对角线交点到正方形一边的距离
2√2
1.已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,
面积S=________.则边长AB=______,
6
36
2.如图,正方形ABCD的周长为15cm,则矩形EFCG的周长为 cm。
7.5
练习1、AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC于F,求证:EC=EF=FB
A
B
C
D
E
F
┌
第十九章 四边形
2、如图在正方形ABCD中,点E,F分别是BC,CD上两点,BE=CF,连接AE,BF交于点G.
求证:①AE=BF
②AE⊥BF
3、已知:正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F
求证:OE=OF
1
2
3
4
5
4、如图(3),正方形ABCD中,AC、BD相交于O,
MN∥AB且MN分别交OA、OB于M、N,
求证:BM=CN。
小结归纳
1
1.利用正方形所特有的对称性结合正方形丰富的边角性质,可以将正方形问题转化为三角形来解决.
2.以三角形来解决四边形的问题是这阶段常用方法.
若正方形A′B′C′D′绕点O旋转某个角度后,OE=OF吗?两正方形重合部分的面积怎样变化?为什么?
中考链接
1
正方形的判定:
四
知道了:什么样的四边形
或平行四边形是正方形
1、定义
2、一组邻边相等+矩形
3、有一个角为直角+菱形
通过本节课的学习,你有哪些收获?
1.正方形的概念
2.正方形的性质
3.解决正方形的有关问题经常将之转化为直角三角形或等腰三角形或全等三角形的问题。
小结归纳
2
1、如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 平方厘米.
A
B
C
D
2、如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.
(1)求证AE=BF;
(2)若BC= cm,求正方形DEFG的边长.
随堂练习
8
满足下列条件的四边形是不是正方形:
1、对角线互相垂直且相等的平行四 边形;
2、对角线互相垂直的矩形;
3、对角线相等的菱形;
4、对角线互相垂直平分且相等的四 边形。
正方形的定义和性质
正方形
矩形---------------有一个角是直角的平行四边形叫做矩形。
菱形------ 有一组邻边相等的平行四边形叫做菱形。
有一个角是直角,有一组邻边相等的平行四边形是什么呢?
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形 是正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
有一个直角
一组邻边相等
一组邻边相等
有一个直角
你能给正方形下一个定义吗?
一个角是直角且一组邻边相等
正方形
1._________________的矩形叫做正方形。
有一组邻边相等
2._________________的菱形叫做正方形。
有一个角是直角
有一组邻边相等并且有一个角是直角
___________________________的平行四边形是正方形。
定义:
四边形
正方与其它四边形的关系
平行四边形
矩形
菱形
正方形
正方形是最特殊的平行四边形
正方形是特殊的矩形
正方形是特殊的菱形
平行四边形
矩形
菱形
正方形
第十九章 四边形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
正方形的性质=
边:
每条对角线平分一组对角。
对边平行
四边相等
四个角都是直角
正方形性质:
角:
对角线:
相等
互相垂直平分
平行四边形
矩形
菱形
正方形
对角线相等
对角线垂直
对角线相等
对角线垂直
对角线垂直且相等
第十九章 四边形
既是中心对称图形轴对称
第十九章 四边形
第十九章 四边形
下列说法对吗?
(1)四个角都相等的四边形是正方形
(2)四条边都相等的四边形是正方形
(3)四边相等,有一角是直角的四边形是正方形
(4) 正方形的一条对角线把正方形分成两个全等的等腰 直角三角形
(5) 正方形是轴对称图形,一共有2条对称轴
正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直.
C、对角互补.
D、对角线相等.
2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直.
C、对角线平分一组对角.
D、对角线相等.
B
D
随堂练习
1. 下列说法是否正确,并说明理由.
①对角线相等的菱形是正方形( )
②对角线互相垂直的矩形是正方形( )
③对角线垂直且相等的平行四边形是正方形( )
④四条边都相等的四边形是正方形( )
⑤四个角相等的四边形是正方形( )
√
√
√
×
×
2. 正方形的四条边______,四个角_______,两条对角线______________________ .
相等
相等
相等且互相垂直平分
判断下列说法是对还是错:
正方形的一条对角线把正方形
分成两个全等的等腰直角三角形。
对
两条对角线呢?
判断下列说法是对还是错:
如果一个矩形的对角线互相垂直,那么它一定是正方形。
对
判断下列说法是对还是错:
如果一个菱形的对角线相等,那么它一定是正方形。
对
判断下列说法是对还是错:
四条边相等,且有一个角是直角的四边形是正方形。
对
四边形再认识
第十九章 四边形
A
B
C
D
O
(2)若AC=4,则正方形边长 ; 正方形的面积是
四边形ABCD是正方形,两条对角线相交于点O,(1)求∠AOB,∠OAB的度数。
8
解:
(1)∵四边形ABCD是正方形
∴AC⊥BD ∠AOB=900
∠BAC=∠DAC
∴∠OAB=450
A
B
C
D
O
E
4㎝
(3)正方形的面积64cm,则对角线交点到正方形一边的距离
2√2
1.已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,
面积S=________.则边长AB=______,
6
36
2.如图,正方形ABCD的周长为15cm,则矩形EFCG的周长为 cm。
7.5
练习1、AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC于F,求证:EC=EF=FB
A
B
C
D
E
F
┌
第十九章 四边形
2、如图在正方形ABCD中,点E,F分别是BC,CD上两点,BE=CF,连接AE,BF交于点G.
求证:①AE=BF
②AE⊥BF
3、已知:正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F
求证:OE=OF
1
2
3
4
5
4、如图(3),正方形ABCD中,AC、BD相交于O,
MN∥AB且MN分别交OA、OB于M、N,
求证:BM=CN。
小结归纳
1
1.利用正方形所特有的对称性结合正方形丰富的边角性质,可以将正方形问题转化为三角形来解决.
2.以三角形来解决四边形的问题是这阶段常用方法.
若正方形A′B′C′D′绕点O旋转某个角度后,OE=OF吗?两正方形重合部分的面积怎样变化?为什么?
中考链接
1
正方形的判定:
四
知道了:什么样的四边形
或平行四边形是正方形
1、定义
2、一组邻边相等+矩形
3、有一个角为直角+菱形
通过本节课的学习,你有哪些收获?
1.正方形的概念
2.正方形的性质
3.解决正方形的有关问题经常将之转化为直角三角形或等腰三角形或全等三角形的问题。
小结归纳
2
1、如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 平方厘米.
A
B
C
D
2、如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.
(1)求证AE=BF;
(2)若BC= cm,求正方形DEFG的边长.
随堂练习
8
