2020_2021学年新教材高中数学阶段提升课第五课概率同步课件新人教A版必修第二册(共29张PPT)
文档属性
| 名称 | 2020_2021学年新教材高中数学阶段提升课第五课概率同步课件新人教A版必修第二册(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 707.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-24 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
阶段提升课
第五课 概 率
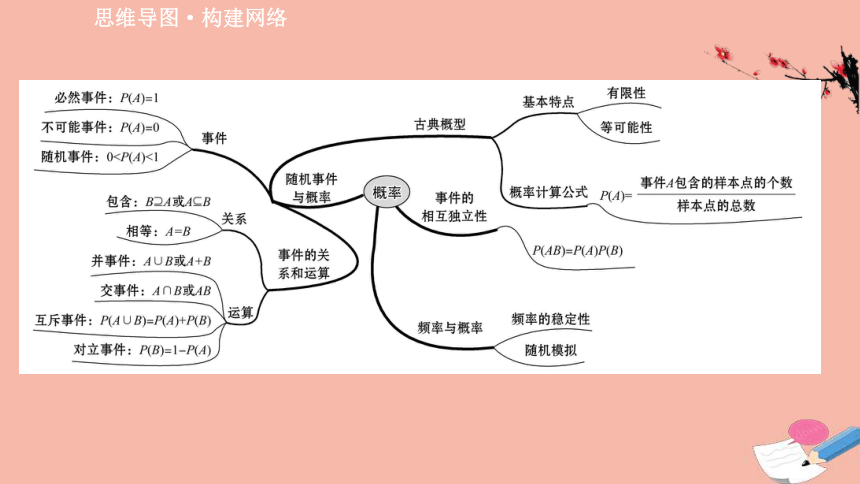
思维导图·构建网络
考点整合·素养提升
题组训练一 事件的关系与运算?
1.根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3.
(1)求该地1位车主至少购买甲、乙两种保险中的1种的概率;
(2)求该地1位车主甲、乙两种保险都不购买的概率.
【解析】记A表示事件:该车主购买甲种保险;B表示事件:该车主购买乙种保险但不购买甲种保险;C表示事件:该车主至少购买甲、乙两种保险中的1种;D表示事件:该车主甲、乙两种保险都不购买.
(1)由题意得P(A)=0.5,P(B)=0.3,又C=A∪B,
所以P(C)=P(A∪B)=P(A)+P(B)=0.5+0.3=0.8.
(2)因为D与C是对立事件,所以P(D)=1-P(C)=1-0.8=0.2.
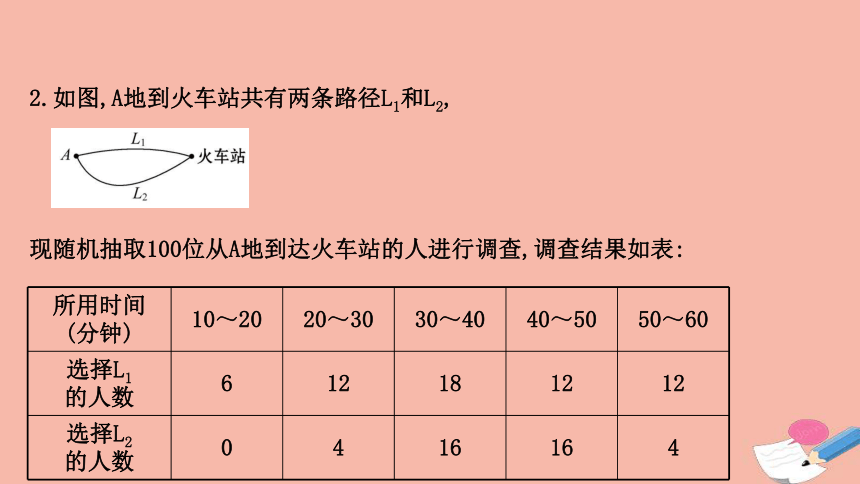
2.如图,A地到火车站共有两条路径L1和L2,
现随机抽取100位从A地到达火车站的人进行调查,调查结果如表:
所用时间
(分钟)
10~20
20~30
30~40
40~50
50~60
选择L1
的人数
6
12
18
12
12
选择L2
的人数
0
4
16
16
4
(1)分别求通过路径L1和L2所用时间落在表中各时间段内的频率.
(2)现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站,为了尽最大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径.
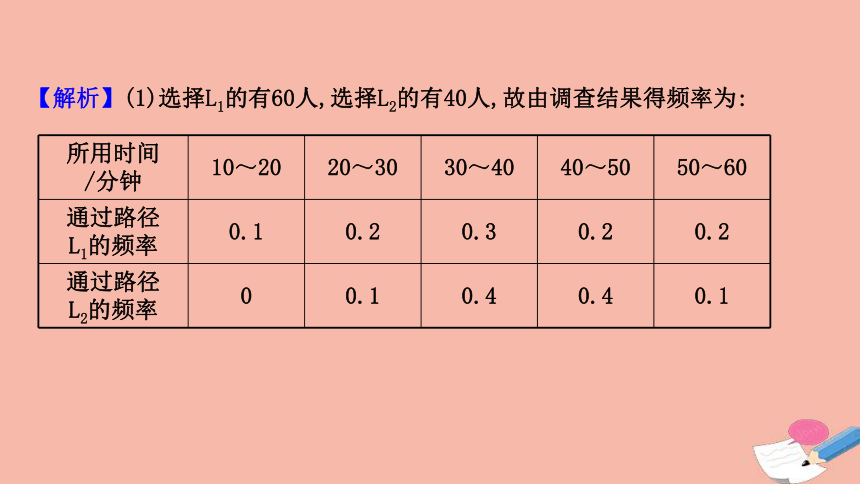
【解析】(1)选择L1的有60人,选择L2的有40人,故由调查结果得频率为:
所用时间
/分钟
10~20
20~30
30~40
40~50
50~60
通过路径
L1的频率
0.1
0.2
0.3
0.2
0.2
通过路径
L2的频率
0
0.1
0.4
0.4
0.1
(2)设A1,A2分别表示甲选择L1和L2时,在40分钟内赶到火车站;
B1,B2分别表示乙选择L1和L2时,在50分钟内赶到火车站.由(1),知P(A1)=0.1+0.2+0.3=0.6,P(A2)=0.1+0.4=0.5,
因为P(A1)>P(A2),所以甲应选择路径L1;
P(B1)=0.1+0.2+0.3+0.2=0.8,
P(B2)=0.1+0.4+0.4=0.9,
因为P(B2)>P(B1),所以乙应选择路径L2.
【方法技巧】
1.互斥事件与对立事件的概率计算
(1)若事件A1,A2,…,An彼此互斥,则P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An).
(2)设事件A的对立事件是
,则P(
)=1-P(A).
2.求复杂事件的概率常用的两种方法
(1)将所求事件转化成彼此互斥的事件的和.
(2)先求其对立事件的概率,然后再应用公式P(
)=1-P(A)求解.
题组训练二 古典概型?
1.甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女.
(1)若从甲校和乙校报名的教师中各任选1名,求选出的2名教师性别相同的概率.
(2)若从报名的6名教师中任选2名,求选出的2名教师来自同一学校的概率.
【解析】(1)从甲校和乙校报名的教师中各任选1名,所有可能的结果为(甲男1,
乙男)、(甲男2,乙男)、(甲男1,乙女1)、(甲男1,乙女2)、(甲男2,乙女1)、
(甲男2,乙女2)、(甲女,乙女1)、(甲女,乙女2)、(甲女,乙男),共9种;选出的2
名教师性别相同的结果有(甲男1,乙男)、(甲男2,乙男)、(甲女,乙女1)、
(甲女,乙女2),共4种,所以选出的2名教师性别相同的概率为
.
(2)从报名的6名教师中任选2名,所有可能的结果为(甲男1,乙男)、(甲男2,乙男)、(甲男1,乙女1)、(甲男1,乙女2)、(甲男2,乙女1)、(甲男2,乙女2)、(甲女,乙女1)、(甲女,乙女2)、(甲女,乙男)、(甲男1,甲男2)、(甲男1,甲女)、(甲男2,甲女)、(乙男,乙女1)、(乙男,乙女2)、(乙女1,乙女2),共15种;选出的2名教师来自同一学校的所有可能的结果为(甲男1,甲男2)、(甲男1,甲女)、(甲男2,甲女)、(乙男,乙女1)、(乙男,乙女2)、(乙女1,乙女2),共6种,所以选出的2名教师来自同一学校的概率为
2.甲、乙二人用4张扑克牌(分别是红桃2、红桃3、红桃4、方片4)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上.甲先抽,乙后抽,各抽一张,抽到的牌不放回.
(1)设(i,j)表示甲、乙抽到的牌的数字,写出甲、乙二人抽到的牌的所有情况.
(2)若甲抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?
(3)甲、乙约定:若甲抽到的牌的牌面数字比乙大,则甲胜;反之,则乙胜.你认为此游戏是否公平,说明你的理由.
【解析】(1)甲、乙二人抽到的牌的所有情况(方片4用4′表示,红桃2、红桃
3、红桃4分别用2,3,4表示)为:(2,3),(2,4),(2,4′),(3,2),(3,4),(3,4′),
(4,2),(4,3),(4,4′),(4′,2),(4′,3),(4′,4),共12种情况.
(2)甲抽到3,乙抽到的牌只能是2或4或4′,因此乙抽到的牌的牌面数字大于3的
概率为
.
(3)甲抽到的牌的牌面数字比乙抽到的牌的牌面数字大的情况有(3,2),(4,2),
(4,3),(4′,2),(4′,3),共5种,所以甲胜的概率为p1=
,乙胜的概率为p2=1-
p1=
.因为
<
,所以此游戏不公平.
【方法技巧】
求解古典概型概率“四步”法
题组训练三 事件的相互独立性?
1.设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.6,0.5,
0.5,0.4,各人是否需使用设备相互独立,则同一工作日至少3人需使用设备的概率为
( )
A.0.25
B.0.30
C.0.31
D.0.35
【解析】选C.设甲、乙、丙、丁需使用设备分别为事件A,B,C,D,则P(A)=0.6,
P(B)=0.5,P(C)=0.5,P(D)=0.4,所以同一工作日最少3人需使用设备的概率为
=0.6×0.5×0.5×0.6+0.6×0.5×0.5×0.4+0.6×0.5×0.5×0.4+0.4×0.5×0.5×0.4+0.6×0.5×0.5×0.4=0.31.
2.某项选拔共有四轮考核,每轮设有一个问题,能正确回答者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三、四轮的问题的概率分别为0.6,0.4,0.5,0.2.已知各轮问题能否正确回答互不影响.
(1)求该选手被淘汰的概率.
(2)求该选手在选拔中至少回答了2个问题后最终被淘汰的概率.
【解析】设“该选手能正确回答第i轮的问题”为事件Ai(i=1,2,3,4),则P(A1)=0.6,P(A2)=0.4,P(A3)=0.5,P(A4)=0.2.
(1)方法一:该选手被淘汰的概率为
=0.4+0.6×0.6+0.6×0.4×0.5+0.6×0.4×0.5×0.8=0.976.
方法二:P=1-P(A1A2A3A4)=1-P(A1)P(A2)·P(A3)P(A4)=1-0.6×0.4×0.5×0.2
=1-0.024=0.976.
(2)方法一:所求概率P=
=0.6×0.6+0.6×0.4×0.5+0.6×0.4×0.5×0.8=0.576.
方法二:所求概率P=1-P(
)-P(A1A2A3A4)=1-(1-0.6)-0.6×0.4×0.5
×0.2=0.576.
【方法技巧】
利用相互独立事件求复杂事件概率的解题思路
(1)将待求复杂事件转化为几个彼此互斥的简单事件的和.
(2)将彼此互斥的简单事件中的简单事件,转化为几个已知(易求)概率的相互独立事件的积事件.
(3)代入概率的积、和公式求解.
题组训练四 频率与概率?
1.为了为奥运会做准备,某射击运动员在相同条件下进行射击训练,结果如表:
射击次数n
10
20
50
100
200
500
击中靶心
次数m
8
19
44
92
178
455
击中靶心
的频率
0.8
0.95
0.88
0.92
0.89
0.91
(1)该射击运动员射击一次,击中靶心的概率大约是多少?
(2)假设该射击运动员射击了300次,则击中靶心的次数大约是多少?
(3)假设该射击运动员射击了10次,前9次中有8次击中靶心,那么第10次一定击中靶心吗?
【解析】(1)由表可知,击中靶心的频率在0.9附近,故击中靶心的概率大约是0.9.
(2)击中靶心的次数大约是300×0.9=270(次).
(3)由概率的意义,可知概率是个常数,不因试验次数的变化而变化.最后一次击中靶心的概率仍是0.9,所以不一定击中靶心.
2.某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如表:
随机调查了该险种的200名续保人在一年内的出险情况,得到统计表:
上年度出
险次数
0
1
2
3
4
≥5
保费
0.85a
a
1.25a
1.5a
1.75a
2a
出险次数
0
1
2
3
4
≥5
频数
60
50
30
30
20
10
(1)记A为事件“一续保人本年度的保费不高于基本保费”.求P(A)的估计值.
(2)记B为事件“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值.
(3)求续保人本年度平均保费的估计值.
【解析】(1)事件A发生当且仅当一年内出险次数小于2.
由所给数据知,一年内出险次数小于2的频率为
=0.55,故P(A)的估计值为
0.55.
(2)事件B发生当且仅当一年内出险次数大于1且小于4.由所给数据知,一年内出
险次数大于1且小于4的频率为
=0.3,故P(B)的估计值为0.3.
(3)由所给数据得
保费
0.85a
a
1.25a
1.5a
1.75a
2a
频率
0.30
0.25
0.15
0.15
0.10
0.05
调查的200名续保人的平均保费为0.85a×0.30+a×0.25+1.25a×0.15+
1.5a×0.15+1.75a×0.10+2a×0.05=1.192
5a.
因此,续保人本年度平均保费的估计值为1.192
5a.
【方法技巧】
(1)依据概率的定义,可以用事件发生的频率去估计概率.
(2)频率的计算公式为fn(A)=
,其中nA是事件A出现的频数,n为重复试验次数.
阶段提升课
第五课 概 率
思维导图·构建网络
考点整合·素养提升
题组训练一 事件的关系与运算?
1.根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3.
(1)求该地1位车主至少购买甲、乙两种保险中的1种的概率;
(2)求该地1位车主甲、乙两种保险都不购买的概率.
【解析】记A表示事件:该车主购买甲种保险;B表示事件:该车主购买乙种保险但不购买甲种保险;C表示事件:该车主至少购买甲、乙两种保险中的1种;D表示事件:该车主甲、乙两种保险都不购买.
(1)由题意得P(A)=0.5,P(B)=0.3,又C=A∪B,
所以P(C)=P(A∪B)=P(A)+P(B)=0.5+0.3=0.8.
(2)因为D与C是对立事件,所以P(D)=1-P(C)=1-0.8=0.2.
2.如图,A地到火车站共有两条路径L1和L2,
现随机抽取100位从A地到达火车站的人进行调查,调查结果如表:
所用时间
(分钟)
10~20
20~30
30~40
40~50
50~60
选择L1
的人数
6
12
18
12
12
选择L2
的人数
0
4
16
16
4
(1)分别求通过路径L1和L2所用时间落在表中各时间段内的频率.
(2)现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站,为了尽最大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径.
【解析】(1)选择L1的有60人,选择L2的有40人,故由调查结果得频率为:
所用时间
/分钟
10~20
20~30
30~40
40~50
50~60
通过路径
L1的频率
0.1
0.2
0.3
0.2
0.2
通过路径
L2的频率
0
0.1
0.4
0.4
0.1
(2)设A1,A2分别表示甲选择L1和L2时,在40分钟内赶到火车站;
B1,B2分别表示乙选择L1和L2时,在50分钟内赶到火车站.由(1),知P(A1)=0.1+0.2+0.3=0.6,P(A2)=0.1+0.4=0.5,
因为P(A1)>P(A2),所以甲应选择路径L1;
P(B1)=0.1+0.2+0.3+0.2=0.8,
P(B2)=0.1+0.4+0.4=0.9,
因为P(B2)>P(B1),所以乙应选择路径L2.
【方法技巧】
1.互斥事件与对立事件的概率计算
(1)若事件A1,A2,…,An彼此互斥,则P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An).
(2)设事件A的对立事件是
,则P(
)=1-P(A).
2.求复杂事件的概率常用的两种方法
(1)将所求事件转化成彼此互斥的事件的和.
(2)先求其对立事件的概率,然后再应用公式P(
)=1-P(A)求解.
题组训练二 古典概型?
1.甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女.
(1)若从甲校和乙校报名的教师中各任选1名,求选出的2名教师性别相同的概率.
(2)若从报名的6名教师中任选2名,求选出的2名教师来自同一学校的概率.
【解析】(1)从甲校和乙校报名的教师中各任选1名,所有可能的结果为(甲男1,
乙男)、(甲男2,乙男)、(甲男1,乙女1)、(甲男1,乙女2)、(甲男2,乙女1)、
(甲男2,乙女2)、(甲女,乙女1)、(甲女,乙女2)、(甲女,乙男),共9种;选出的2
名教师性别相同的结果有(甲男1,乙男)、(甲男2,乙男)、(甲女,乙女1)、
(甲女,乙女2),共4种,所以选出的2名教师性别相同的概率为
.
(2)从报名的6名教师中任选2名,所有可能的结果为(甲男1,乙男)、(甲男2,乙男)、(甲男1,乙女1)、(甲男1,乙女2)、(甲男2,乙女1)、(甲男2,乙女2)、(甲女,乙女1)、(甲女,乙女2)、(甲女,乙男)、(甲男1,甲男2)、(甲男1,甲女)、(甲男2,甲女)、(乙男,乙女1)、(乙男,乙女2)、(乙女1,乙女2),共15种;选出的2名教师来自同一学校的所有可能的结果为(甲男1,甲男2)、(甲男1,甲女)、(甲男2,甲女)、(乙男,乙女1)、(乙男,乙女2)、(乙女1,乙女2),共6种,所以选出的2名教师来自同一学校的概率为
2.甲、乙二人用4张扑克牌(分别是红桃2、红桃3、红桃4、方片4)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上.甲先抽,乙后抽,各抽一张,抽到的牌不放回.
(1)设(i,j)表示甲、乙抽到的牌的数字,写出甲、乙二人抽到的牌的所有情况.
(2)若甲抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?
(3)甲、乙约定:若甲抽到的牌的牌面数字比乙大,则甲胜;反之,则乙胜.你认为此游戏是否公平,说明你的理由.
【解析】(1)甲、乙二人抽到的牌的所有情况(方片4用4′表示,红桃2、红桃
3、红桃4分别用2,3,4表示)为:(2,3),(2,4),(2,4′),(3,2),(3,4),(3,4′),
(4,2),(4,3),(4,4′),(4′,2),(4′,3),(4′,4),共12种情况.
(2)甲抽到3,乙抽到的牌只能是2或4或4′,因此乙抽到的牌的牌面数字大于3的
概率为
.
(3)甲抽到的牌的牌面数字比乙抽到的牌的牌面数字大的情况有(3,2),(4,2),
(4,3),(4′,2),(4′,3),共5种,所以甲胜的概率为p1=
,乙胜的概率为p2=1-
p1=
.因为
<
,所以此游戏不公平.
【方法技巧】
求解古典概型概率“四步”法
题组训练三 事件的相互独立性?
1.设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.6,0.5,
0.5,0.4,各人是否需使用设备相互独立,则同一工作日至少3人需使用设备的概率为
( )
A.0.25
B.0.30
C.0.31
D.0.35
【解析】选C.设甲、乙、丙、丁需使用设备分别为事件A,B,C,D,则P(A)=0.6,
P(B)=0.5,P(C)=0.5,P(D)=0.4,所以同一工作日最少3人需使用设备的概率为
=0.6×0.5×0.5×0.6+0.6×0.5×0.5×0.4+0.6×0.5×0.5×0.4+0.4×0.5×0.5×0.4+0.6×0.5×0.5×0.4=0.31.
2.某项选拔共有四轮考核,每轮设有一个问题,能正确回答者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三、四轮的问题的概率分别为0.6,0.4,0.5,0.2.已知各轮问题能否正确回答互不影响.
(1)求该选手被淘汰的概率.
(2)求该选手在选拔中至少回答了2个问题后最终被淘汰的概率.
【解析】设“该选手能正确回答第i轮的问题”为事件Ai(i=1,2,3,4),则P(A1)=0.6,P(A2)=0.4,P(A3)=0.5,P(A4)=0.2.
(1)方法一:该选手被淘汰的概率为
=0.4+0.6×0.6+0.6×0.4×0.5+0.6×0.4×0.5×0.8=0.976.
方法二:P=1-P(A1A2A3A4)=1-P(A1)P(A2)·P(A3)P(A4)=1-0.6×0.4×0.5×0.2
=1-0.024=0.976.
(2)方法一:所求概率P=
=0.6×0.6+0.6×0.4×0.5+0.6×0.4×0.5×0.8=0.576.
方法二:所求概率P=1-P(
)-P(A1A2A3A4)=1-(1-0.6)-0.6×0.4×0.5
×0.2=0.576.
【方法技巧】
利用相互独立事件求复杂事件概率的解题思路
(1)将待求复杂事件转化为几个彼此互斥的简单事件的和.
(2)将彼此互斥的简单事件中的简单事件,转化为几个已知(易求)概率的相互独立事件的积事件.
(3)代入概率的积、和公式求解.
题组训练四 频率与概率?
1.为了为奥运会做准备,某射击运动员在相同条件下进行射击训练,结果如表:
射击次数n
10
20
50
100
200
500
击中靶心
次数m
8
19
44
92
178
455
击中靶心
的频率
0.8
0.95
0.88
0.92
0.89
0.91
(1)该射击运动员射击一次,击中靶心的概率大约是多少?
(2)假设该射击运动员射击了300次,则击中靶心的次数大约是多少?
(3)假设该射击运动员射击了10次,前9次中有8次击中靶心,那么第10次一定击中靶心吗?
【解析】(1)由表可知,击中靶心的频率在0.9附近,故击中靶心的概率大约是0.9.
(2)击中靶心的次数大约是300×0.9=270(次).
(3)由概率的意义,可知概率是个常数,不因试验次数的变化而变化.最后一次击中靶心的概率仍是0.9,所以不一定击中靶心.
2.某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如表:
随机调查了该险种的200名续保人在一年内的出险情况,得到统计表:
上年度出
险次数
0
1
2
3
4
≥5
保费
0.85a
a
1.25a
1.5a
1.75a
2a
出险次数
0
1
2
3
4
≥5
频数
60
50
30
30
20
10
(1)记A为事件“一续保人本年度的保费不高于基本保费”.求P(A)的估计值.
(2)记B为事件“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值.
(3)求续保人本年度平均保费的估计值.
【解析】(1)事件A发生当且仅当一年内出险次数小于2.
由所给数据知,一年内出险次数小于2的频率为
=0.55,故P(A)的估计值为
0.55.
(2)事件B发生当且仅当一年内出险次数大于1且小于4.由所给数据知,一年内出
险次数大于1且小于4的频率为
=0.3,故P(B)的估计值为0.3.
(3)由所给数据得
保费
0.85a
a
1.25a
1.5a
1.75a
2a
频率
0.30
0.25
0.15
0.15
0.10
0.05
调查的200名续保人的平均保费为0.85a×0.30+a×0.25+1.25a×0.15+
1.5a×0.15+1.75a×0.10+2a×0.05=1.192
5a.
因此,续保人本年度平均保费的估计值为1.192
5a.
【方法技巧】
(1)依据概率的定义,可以用事件发生的频率去估计概率.
(2)频率的计算公式为fn(A)=
,其中nA是事件A出现的频数,n为重复试验次数.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
