2020_2021学年新教材高中数学阶段提升课第四课统计同步课件新人教A版必修第二册(共29张PPT)
文档属性
| 名称 | 2020_2021学年新教材高中数学阶段提升课第四课统计同步课件新人教A版必修第二册(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 538.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-24 20:43:59 | ||
图片预览








文档简介
(共29张PPT)
阶段提升课
第四课 统 计
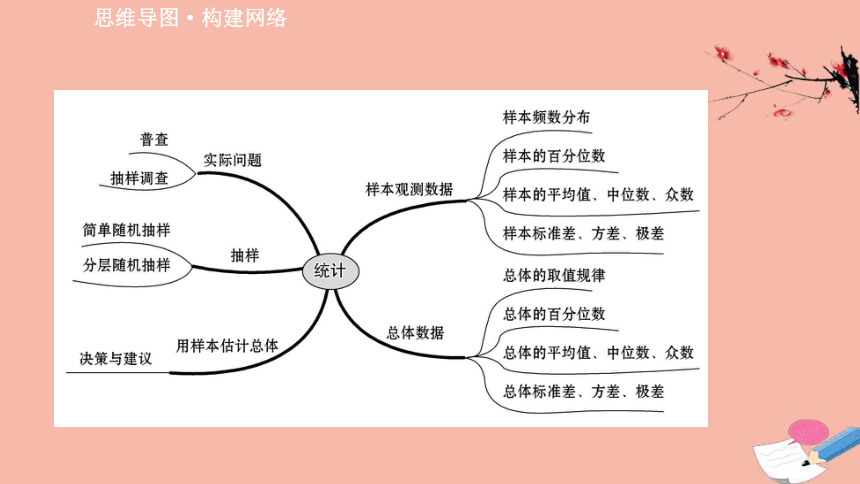
思维导图·构建网络
考点整合·素养提升
题组训练一 随机抽样?
1.上海某中学从40名学生中选1人作为上海男篮拉拉队的成员,采用下面两种选法:
选法一 将这40名学生从1~40进行编号,相应地制作1~40的40个号签,把这40个号签放在一个暗箱中搅匀,最后随机地从中抽取1个号签,与这个号签一致的学生幸运入选;
选法二 将39个白球与1个红球(球除颜色外,其他完全相同)混合放在一个暗箱中搅匀,让40名学生逐一从中摸取一球,摸到红球的学生成为拉拉队成员.
试问这两种选法是否都是抽签法?为什么?这两种选法有何异同?
【解析】选法一满足抽签法的特征,是抽签法;选法二不是抽签法.因为抽签法
要求所有的号签编号互不相同,而选法二中39个白球无法相互区分.这两种选法
相同之处在于每名学生被选中的可能性都相等,均为
.
2.某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多
参加其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占
10%.登山组的职工占参加活动总人数的
,且该组中青年人占50%,中年人占40%,
老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用
分层随机抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确
定:
(1)游泳组中,青年人、中年人、老年人分别所占的比例.
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
【解析】(1)设登山组人数为x,游泳组中,青年人、中年人、
老年人所占比例分别为a,b,c,
则有
=47.5%,
=10%,
解得b=0.5,c=0.1,故a=1-0.5-0.1=0.4,
即游泳组中,青年人、中年人、老年人所占比例分别为40%,50%,10%.
(2)游泳组中,抽取的青年人人数为200×
×40%=60(人);
抽取的中年人人数为200×
×50%=75(人);
抽取的老年人人数为200×
×10%=15(人).
即游泳组中,青年人、中年人、老年人分别应抽取的人数为60人,75人,15人.
【方法技巧】
抽样方法的特点及选取规则:
简单随机抽样和比例分配的分层随机抽样的共同特点是在抽样过程中每个个体被抽取的机会相等,
(1)特点:体现了这些抽样方法的客观性和公平性.
(2)规则:当总体中的个体数较少时,常采用简单随机抽样;当已知总体由差异明显的几部分组成时,常采用分层随机抽样.在进行分层随机抽样时要用到简单随机抽样方法.
题组训练二 利用样本的频率分布估计总体的取值规律?
1.为了研究某药品的疗效,选取若干名志愿者进行临床试验.所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,…,第五组.如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为
( )
A.6
B.8
C.12
D.18
【解析】选C.由题图可知,第一组和第二组的频率之和为(0.24+0.16)×1=0.40,
故该试验共选取的志愿者有
=50人.所以第三组共有50×0.36=18人,其中有
疗效的人数为18-6=12人.
2.为了让学生了解更多有关“一带一路”倡议的信息,某中学举行了一次“丝绸之路知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表,解答下列问题:
分组
频数
频率
60.5~70.5
0.16
70.5~80.5
10
80.5~90.5
18
0.36
90.5~100.5
合计
(1)填充频率分布表中的空格(将答案直接填在表格内),并作出频率分布直方图.
(2)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约有多少名?
【解析】(1)频率分布表如表所示,
频率分布直方图如图所示.
分组
频数
频率
60.5~70.5
8
0.16
70.5~80.5
10
0.20
80.5~90.5
18
0.36
90.5~100.5
14
0.28
合计
50
1
(2)在被抽到的学生成绩中,在85.5~95.5分的个数约是9+7=16,占样本的比例
是
=0.32,即获得二等奖的概率约为32%,所以获得二等奖的学生约有800×
32%=256(名).
【方法技巧】
总体频率分布的估计方法:
(1)频率为小矩形的面积,利用频率可以计算样本容量、频数等.
(2)所有小矩形的面积(频率)之和为1.
题组训练三 利用样本的百分位数估计总体的百分位数?
一家保险公司决定对推销员实行目标管理,即给推销员确定一个具体的销售目标.确定的销售目标是否合适,直接影响到公司的经济效益.如果目标定得过高,多数推销员完不成任务,会使推销员失去信心;如果目标定得太低,将不利于挖掘推销员的工作潜力.下面一组数据是部分推销员的月销售额(单位:千元).
19.58 16.11 16.45 20.45 20.24 21.66 22.45
18.22 12.34
19.35 20.55 17.45 18.78 17.96 19.91 18.12
14.65 14.78
16.78 18.78 18.29 18.51 17.86 19.58 19.21
18.55 16.34
15.54 17.55 14.89 18.94 17.43 17.14 18.02
19.98 17.88
17.32 19.35 15.45 19.58 13.45 21.34 14.00
18.42 23.00
17.52 18.51 17.16 24.56 25.14
请根据这组样本数据提出使65%的职工能够完成销售指标的建议.
【解析】将这50个样本数据按从小到大排序,可得
12.34 13.45 14.00 14.65 14.78 14.89 15.45
15.54 16.11
16.34 16.45 16.78 17.14 17.16 17.32 17.43
17.45 17.52
17.55 17.86 17.88 17.96 18.02 18.12 18.22
18.29 18.42
18.51 18.51 18.55 18.78 18.78 18.94 19.21
19.35 19.35
19.58 19.58 19.58 19.91 19.98 20.24 20.45
20.55 21.34
21.66 22.45 23.00 24.56 25.14
有65%的职工能够完成销售指标,那么35%的职工不能完成销售指标.
由50×(1-65%)=17.5可知这组数据的35%分位数为17.52.故为使65%的职工能够完成销售指标,该保险公司可将月销售额定为17.52千元.
【方法技巧】
计算一组n个数据的第p百分位数的一般步骤:
第1步,按从小到大排列原始数据.
第2步,计算i=n×p%.
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
题组训练四 利用样本估计总体的集中趋势和离散程度?
1.我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中a的值.
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月均用水量的中位数.
【解析】(1)由频率分布直方图,可知月均用水量在[0,0.5)的频率为0.08×0.5=0.04.
同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5]组内的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.
由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=0.5×a+0.5×a,解得a=0.30.
(2)由(1),100位居民月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12,
由以上样本的频率分布,可以估计30万居民中月均用水量不低于3吨的人数为300
000×0.12=36
000.
(3)设中位数为x吨.
因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,
而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,所以2≤x<2.5.
由0.50×(x-2)=0.5-0.48,解得x=2.04.
故可估计居民月均用水量的中位数为2.04吨.
2.甲、乙两机床同时加工直径为100
cm的零件,为检验质量,各从中抽取6件测量,数据为:
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
(1)分别计算两组数据的平均数及方差.
(2)根据计算结果判断哪台机床加工零件的质量更稳定.
【解析】(1)
=
×(99+100+98+100+100+103)=100,
=
×(99+100+102+99+100+100)=100.
=
×[(99-100)2+(100-100)2+(98-100)2+(100-100)2+(100-100)2+
(103-100)2]=
,
=
×[(99-100)2+(100-100)2+(102-100)2+(99-100)2+(100-100)2+
(100-100)2]=1.
(2)两台机床所加工零件的直径的平均数相同,
又
>
,所以乙机床加工零件的质量更稳定.
【方法技巧】
利用样本数据的众数、中位数、平均数和标准差等估计总体问题
(1)平均数、众数、中位数都是描述一组数据的特点,但描述的含义不同.
(2)标准差、方差都是描述一组数据波动情况的量,越小就表示越稳定.
阶段提升课
第四课 统 计
思维导图·构建网络
考点整合·素养提升
题组训练一 随机抽样?
1.上海某中学从40名学生中选1人作为上海男篮拉拉队的成员,采用下面两种选法:
选法一 将这40名学生从1~40进行编号,相应地制作1~40的40个号签,把这40个号签放在一个暗箱中搅匀,最后随机地从中抽取1个号签,与这个号签一致的学生幸运入选;
选法二 将39个白球与1个红球(球除颜色外,其他完全相同)混合放在一个暗箱中搅匀,让40名学生逐一从中摸取一球,摸到红球的学生成为拉拉队成员.
试问这两种选法是否都是抽签法?为什么?这两种选法有何异同?
【解析】选法一满足抽签法的特征,是抽签法;选法二不是抽签法.因为抽签法
要求所有的号签编号互不相同,而选法二中39个白球无法相互区分.这两种选法
相同之处在于每名学生被选中的可能性都相等,均为
.
2.某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多
参加其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占
10%.登山组的职工占参加活动总人数的
,且该组中青年人占50%,中年人占40%,
老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用
分层随机抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确
定:
(1)游泳组中,青年人、中年人、老年人分别所占的比例.
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
【解析】(1)设登山组人数为x,游泳组中,青年人、中年人、
老年人所占比例分别为a,b,c,
则有
=47.5%,
=10%,
解得b=0.5,c=0.1,故a=1-0.5-0.1=0.4,
即游泳组中,青年人、中年人、老年人所占比例分别为40%,50%,10%.
(2)游泳组中,抽取的青年人人数为200×
×40%=60(人);
抽取的中年人人数为200×
×50%=75(人);
抽取的老年人人数为200×
×10%=15(人).
即游泳组中,青年人、中年人、老年人分别应抽取的人数为60人,75人,15人.
【方法技巧】
抽样方法的特点及选取规则:
简单随机抽样和比例分配的分层随机抽样的共同特点是在抽样过程中每个个体被抽取的机会相等,
(1)特点:体现了这些抽样方法的客观性和公平性.
(2)规则:当总体中的个体数较少时,常采用简单随机抽样;当已知总体由差异明显的几部分组成时,常采用分层随机抽样.在进行分层随机抽样时要用到简单随机抽样方法.
题组训练二 利用样本的频率分布估计总体的取值规律?
1.为了研究某药品的疗效,选取若干名志愿者进行临床试验.所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,…,第五组.如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为
( )
A.6
B.8
C.12
D.18
【解析】选C.由题图可知,第一组和第二组的频率之和为(0.24+0.16)×1=0.40,
故该试验共选取的志愿者有
=50人.所以第三组共有50×0.36=18人,其中有
疗效的人数为18-6=12人.
2.为了让学生了解更多有关“一带一路”倡议的信息,某中学举行了一次“丝绸之路知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表,解答下列问题:
分组
频数
频率
60.5~70.5
0.16
70.5~80.5
10
80.5~90.5
18
0.36
90.5~100.5
合计
(1)填充频率分布表中的空格(将答案直接填在表格内),并作出频率分布直方图.
(2)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约有多少名?
【解析】(1)频率分布表如表所示,
频率分布直方图如图所示.
分组
频数
频率
60.5~70.5
8
0.16
70.5~80.5
10
0.20
80.5~90.5
18
0.36
90.5~100.5
14
0.28
合计
50
1
(2)在被抽到的学生成绩中,在85.5~95.5分的个数约是9+7=16,占样本的比例
是
=0.32,即获得二等奖的概率约为32%,所以获得二等奖的学生约有800×
32%=256(名).
【方法技巧】
总体频率分布的估计方法:
(1)频率为小矩形的面积,利用频率可以计算样本容量、频数等.
(2)所有小矩形的面积(频率)之和为1.
题组训练三 利用样本的百分位数估计总体的百分位数?
一家保险公司决定对推销员实行目标管理,即给推销员确定一个具体的销售目标.确定的销售目标是否合适,直接影响到公司的经济效益.如果目标定得过高,多数推销员完不成任务,会使推销员失去信心;如果目标定得太低,将不利于挖掘推销员的工作潜力.下面一组数据是部分推销员的月销售额(单位:千元).
19.58 16.11 16.45 20.45 20.24 21.66 22.45
18.22 12.34
19.35 20.55 17.45 18.78 17.96 19.91 18.12
14.65 14.78
16.78 18.78 18.29 18.51 17.86 19.58 19.21
18.55 16.34
15.54 17.55 14.89 18.94 17.43 17.14 18.02
19.98 17.88
17.32 19.35 15.45 19.58 13.45 21.34 14.00
18.42 23.00
17.52 18.51 17.16 24.56 25.14
请根据这组样本数据提出使65%的职工能够完成销售指标的建议.
【解析】将这50个样本数据按从小到大排序,可得
12.34 13.45 14.00 14.65 14.78 14.89 15.45
15.54 16.11
16.34 16.45 16.78 17.14 17.16 17.32 17.43
17.45 17.52
17.55 17.86 17.88 17.96 18.02 18.12 18.22
18.29 18.42
18.51 18.51 18.55 18.78 18.78 18.94 19.21
19.35 19.35
19.58 19.58 19.58 19.91 19.98 20.24 20.45
20.55 21.34
21.66 22.45 23.00 24.56 25.14
有65%的职工能够完成销售指标,那么35%的职工不能完成销售指标.
由50×(1-65%)=17.5可知这组数据的35%分位数为17.52.故为使65%的职工能够完成销售指标,该保险公司可将月销售额定为17.52千元.
【方法技巧】
计算一组n个数据的第p百分位数的一般步骤:
第1步,按从小到大排列原始数据.
第2步,计算i=n×p%.
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
题组训练四 利用样本估计总体的集中趋势和离散程度?
1.我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中a的值.
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月均用水量的中位数.
【解析】(1)由频率分布直方图,可知月均用水量在[0,0.5)的频率为0.08×0.5=0.04.
同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5]组内的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.
由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=0.5×a+0.5×a,解得a=0.30.
(2)由(1),100位居民月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12,
由以上样本的频率分布,可以估计30万居民中月均用水量不低于3吨的人数为300
000×0.12=36
000.
(3)设中位数为x吨.
因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,
而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,所以2≤x<2.5.
由0.50×(x-2)=0.5-0.48,解得x=2.04.
故可估计居民月均用水量的中位数为2.04吨.
2.甲、乙两机床同时加工直径为100
cm的零件,为检验质量,各从中抽取6件测量,数据为:
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
(1)分别计算两组数据的平均数及方差.
(2)根据计算结果判断哪台机床加工零件的质量更稳定.
【解析】(1)
=
×(99+100+98+100+100+103)=100,
=
×(99+100+102+99+100+100)=100.
=
×[(99-100)2+(100-100)2+(98-100)2+(100-100)2+(100-100)2+
(103-100)2]=
,
=
×[(99-100)2+(100-100)2+(102-100)2+(99-100)2+(100-100)2+
(100-100)2]=1.
(2)两台机床所加工零件的直径的平均数相同,
又
>
,所以乙机床加工零件的质量更稳定.
【方法技巧】
利用样本数据的众数、中位数、平均数和标准差等估计总体问题
(1)平均数、众数、中位数都是描述一组数据的特点,但描述的含义不同.
(2)标准差、方差都是描述一组数据波动情况的量,越小就表示越稳定.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
